吴恩达机器学习笔记(6)——Logistic回归
1. Classification
我们可以尝试使用线性回归来实现分类,所要做的就是在线性回归拟合数据以后给他一个threshold(阈值),例如在下面的例子中,就可以给一个0.5作为阈值(当hθ(x)的值大于等于0.5时,预测y为1;当hθ(x)小于0.5时,预测y为0)来预测肿瘤的性质(良性或恶性)。
在这种情况下,我们所看到的使用线性回归来实现分类任务好像没有问题,但是,当我们多了一个训练样本时,显然我们这个(旧的)假设仍然很好(即所有在0.5上方的预测为1,在下方的预测为0)
但是如果我们运行线性回归,我们会得到一条不一样的拟合直线(蓝色),如下图,如果这个时候我们仍然取threshold为0.5,那么这个对应点在x轴的位置会右移,这个时候我们的分类就出现问题了。
所以说,将线性回归用于分类(Classification)通常(often)不是一个好主意。
而且在分类中,Y∈{0,1},但是如果使用线性回归的话,hθ(x)的值可能会远大于1或远小于0,这可能会使分类看起来很奇怪。
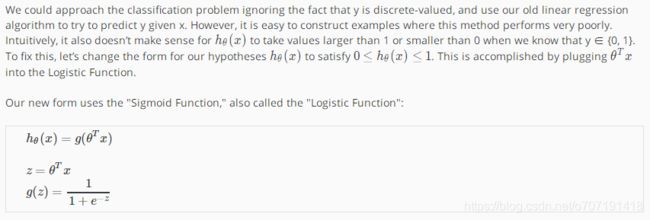
这时候,引出了Logistics Regression算法,该算法的输出值会介于0和1之间。
虽然名字里有regression,但实际是一种分类(Classification)算法,名字是出于历史原因而命名的(Logistic Function)。
2. Hypothesis Representation
使用这个Logistic Function(上图中的g(z),也叫做sigmoid function),可以将我们的函数输出值限定在(0,1)之间,下面是它的函数图像。
所以现在的hθ(x)的意义是预测值为1的概率,例如,hθ(x)=0.7表示有70%的可能使得y=1,其数学表达式如下:
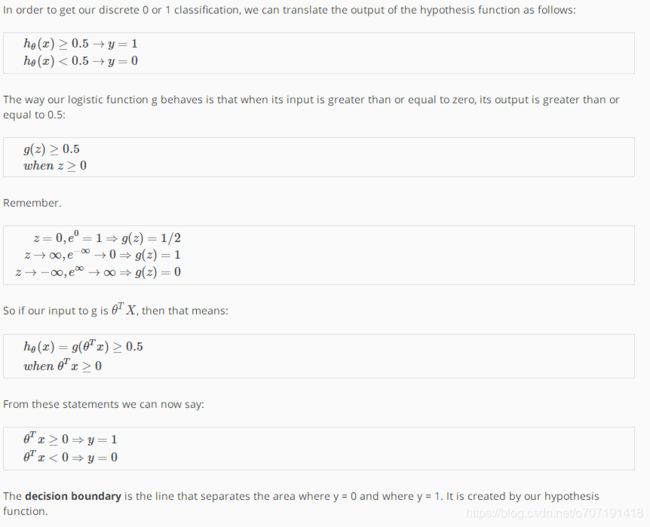
3. Decision Boundary
决策边界就是将y=0和y=1分开的line,可能是直线也可能是曲线。
上图中,粉红色的直线就是决策边界。
在视频里,有一句话吴恩达老师一直在强调——决策边界并不是训练集的属性,而是假设函数(hθ(x))的一个属性,由其参数θ 决定。
4. Cost Function
如果我们使用前面线性回归所使用的代价函数来进行计算,那么会出现如下图所示的问题,因为假设函数sigmoid function是一个(非常)非线性函数,所以当代入到线性回归的代价函数中后,会使得代价函数J变得像下图左边图像所示,有很多的局部最小值,这样一来,使用梯度下降法就很难收敛到全局最小值了。那么我们就希望能够找到一个适合Logistic Regression的代价函数,使得其函数图像是一个凹函数(如下图右边图像所示)。这时如果我们使用梯度下降算法,就能够收敛到全局最小值。
因此,将Logistic regression的代价函数定义如下
可以看到当hθ(x)趋于0时,代价函数趋于无穷大,此时的含义代表当我们有几乎100%把握确定这个事件时,却发现预测错误,那么惩罚会增加到无穷大;而当预测完全正确时,代价函数则会降为0。
5. Simplified Cost Function and Gradient Descent
前面把logistic回归的Cost部分写成了下面的形式:
显然这种形式有些复杂,不便于求解,因此将这两个式子统一起来写成一个等式:
当y=0和y=1时就分别对应上面的代价函数,简化了许多。因此,代价函数就变成了下面的形式(以及向量化形式):
那么,其梯度下降算法就可以很容易得到:
其向量化形式为:
在Coursera的lecture里也给出了求偏导数的公式:
通过这个求导公式可以看出,式中的log其实就是我们所用的ln!
同样的,使用这个向量化公式,可以非常简洁地写出matlab代码:
6. Advanced Optimization
这一部分,主要讲了几个优化算法的用法,这些算法涉及到数值计算的问题,所以就没有深入讲解,只是这些优化算法的计算速度会比梯度下降算法快很多。
7.Multiclass Classification: One-vs-all
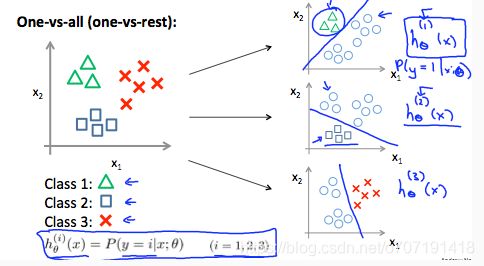
前面所讲的分类都是二分类(binary-classification)问题,这里吴恩达老师简单地提了一下多分类的方法——one-verses-all。
比如现在有一个四个类别的分类问题,例如将学生成绩分为Perfect、Good、Not bad、awful四个等级,那么对应的可以将y的输出值设为y=0,1,2,3分别对应这四个类别。
这里主要还是运用了二分类的思想,我们可以在四个类别中提取出一个类别(设为positive),另外三个组成一个类别(设为negative),然后使用二分类的方法将其分开。
对于每一个类别都重复上面的步骤一次,那么一共可以做4次二分类,对应的得到四个结果:
也就得到了上式中的n取3的情况,
那么当我们进行预测时,将特征X分别输入进这四个分类器,会得到四个hθ(x)的值,在这些值中取出最大的那个,就是我们所想要的分类结果。