数学建模笔记——插值拟合模型(二)
今天是8月21日,距离上次写文章好像将近一个月了……这段时间经历了建模校内选拔赛,考试周,以及与网络小说的斗智斗勇……好吧,其实也没干什么,除了考试就是荒废……
我最近有在思考一个问题,就是我所关注的知识输出型公众号,知乎专栏啊,其作者绝大部分都是在相应的领域打拼多年或者取得一定成绩的人。然而我只是一个平平无奇无奖项无经历无成就的大学生,这让我怀疑我现在是不是不太适合写这些,例如努力拿个建模奖之后再回来写,会不会更有底气?其实我做的是什么呢?无非就是介绍搬运一些许多书上已经有的,经过了无数年的沉淀的知识。如果愿意的话,完全可以找一本相关书籍,在几天之内浏览完毕,感觉跟看我写的小白型文章是差不多的效果。所以有些时候也会怀疑做这些是不是没太大意义……
不过不管怎么说,当时立下的flag就是写一个数学建模笔记系列,那还是要尽量完成的。今天就延续之前的内容,讲一讲“拟合”这个话题。
什么是拟合
上节课我们提到了插值,所谓插值,就是在已知有限个数据点 ( x i , y i ) (x_i,y_i) (xi,yi)的前提下,通过使用简单函数代替复杂或者未知函数的想法,去推测其他点 x j x_j xj所对应的 y j y_j yj值。但插值函数有一些问题,例如,若插值函数次数过高,会出现龙格现象,也就是预测值波动较大。而如果我们使用了分段插值来降低插值函数的次数,那我们所能做出的推测,往往只是在相应的插值节点形成的区间内部,也就是分段逼近了原函数,而段外的则没有足够的信息去近似。例如,我们知道了 [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 ] [1,2,3,4,5,6,7,8,9,10] [1,2,3,4,5,6,7,8,9,10]这10个横坐标对应的 y y y值,此时让我们估计 x = 3.36 x=3.36 x=3.36对应的值是相对比较简单的,分段插值即可。而让我们估计 x = 20.25 x=20.25 x=20.25所对应的值,就相对不那么具有合理性了,因为这个点离已知点实在比较远,且中间一部分信息也是未知的。
那什么是拟合呢?拟合类似于插值,都是函数逼近的一种手段。区别在于,插值函数必须经过所有已知点,而拟合得到的函数,只需要满足在某种意义下,已知点与该函数曲线的“误差”最小。换句话说,拟合就是在平面上找到一条连续的曲线,使得所有已知点到这条曲线的总距离最小。这样我们就有理由使用这条曲线来近似原函数曲线了。
如上图所示,对于上面的14个样本点,我们如果使用分段线性插值逼近原函数,就得到了一条分段的线性函数。而如果使用一元线性拟合逼近原函数,就得到了一条完整的直线,且所有已知点距离这条直线的总距离最小,也就是总的偏差最小。
不止是线性拟合,我们也可以使用指数函数的形式 f ( x ) = a e b x m + c + d f(x)=ae^{bx^m+c}+d f(x)=aebxm+c+d或者逻辑斯蒂函数 f ( x ) = a 1 + c e − b x f(x)=\frac{a}{1+ce^{-bx}} f(x)=1+ce−bxa或者其他任何形式的函数进行拟合,以实其更加符合实际问题的需要。而插值往往只使用多项式插值或者三角函数插值。
一元线性拟合
之后我们来谈一谈拟合的原理,以一元线性拟合为例。
如上图所示,所谓的一元线性拟合,就是找到一条直线 y = k x + b y=kx+b y=kx+b使得所有的已知点与该直线的总距离最小,也就是总偏差最小。换句话说,就是在上图平面中,无数的黑线内(这里只画了几条,但 y = k x + b y=kx+b y=kx+b很明显是代表无数条直线的),找到一条最接近原函数的直线。
所以,问题的关键就在于,我们用什么指标来衡量,已知点与曲线之间的总距离(偏差)。嗯,是一个很经典的方法,高中应该就学过的——最小二乘法。
如图,不妨设 y ^ = k ^ x + b ^ \hat{y}=\hat{k}x+\hat{b} y^=k^x+b^代表我们拟合出的曲线,于是我们可以定义 ∣ y i − y i ^ ∣ |y_i-\hat{y_i}| ∣yi−yi^∣也即 ∣ y i − ( k ^ x i + b ^ ) ∣ |y_i-(\hat{k}x_i+\hat{b})| ∣yi−(k^xi+b^)∣来代表点 ( x i , y i ) (x_i,y_i) (xi,yi)与直线的距离,也就是用,相同 x x x的情况下, y y y的拟合值与实际值之差的绝对值来衡量距离。应该很好理解吧。其实就是上图中黑色线段的长度了。
因此,假设有 n n n个已知点,那已知点与曲线的总偏差就是 ∑ i = 1 n ∣ y i − y ^ i ∣ \sum_{i=1}^n|y_i-\hat{y}_i| ∑i=1n∣yi−y^i∣,我们的优化问题就是 A r g m i n k ^ , b ^ ∑ i = 1 n ∣ y i − y ^ i ∣ \mathop{Argmin}\limits_{\hat{k},\hat{b}}\sum_{i=1}^n|y_i-\hat{y}_i| k^,b^Argmin∑i=1n∣yi−y^i∣,也就是求解相应的 k ^ , b ^ \hat{k},\hat{b} k^,b^使得总偏差最小。考虑到带绝对值的优化问题求解起来不太方便,因此我们用 ( y i − y ^ i ) 2 (y_i-\hat{y}_i)^2 (yi−y^i)2来代表距离,也就是绝对值的平方。这样,优化问题就转化为 A r g m i n k ^ , b ^ ∑ i = 1 n ( y i − y ^ i ) 2 \mathop{Argmin}\limits_{\hat{k},\hat{b}}\sum_{i=1}^n(y_i-\hat{y}_i)^2 k^,b^Argmin∑i=1n(yi−y^i)2,其中 y ^ = k ^ x + b ^ \hat{y}=\hat{k}x+\hat{b} y^=k^x+b^。这也就是最小二乘法在一元拟合上的应用,即寻求参数使得相同 x x x情况下,拟合值与实际值之差的平方和最小。
之后就是如何求解该优化问题了。这是一个二元函数求最小值的问题,使用微积分的相关定理即可,此处不做详细介绍。下面放上一个简要的过程。




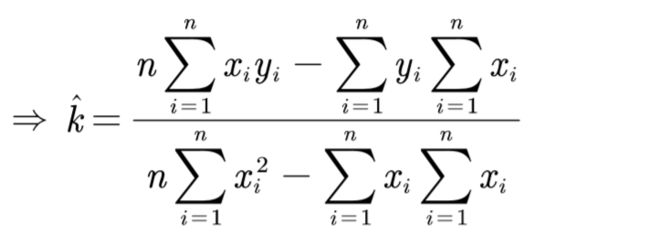
由上图的公式求出 k ^ \hat{k} k^之后, b ^ = y ˉ − k ^ x ˉ \hat{b}=\bar{y}-\hat{k}\bar{x} b^=yˉ−k^xˉ,其中 y ˉ = 1 n ∑ i = 1 n y i , x ˉ = 1 n ∑ i = 1 n x i \bar{y}=\frac{1}{n}\sum_{i=1}^ny_i,\bar{x}=\frac{1}{n}\sum_{i=1}^nx_i yˉ=n1∑i=1nyi,xˉ=n1∑i=1nxi。即 ( x ˉ , y ˉ ) (\bar{x},\bar{y}) (xˉ,yˉ)一定位于该拟合直线上,这一点的证明也可以在上图中找到的。
非线性函数的线性化
在实际的问题中, x , y x,y x,y之间并不一定是线性关系,但如果我们知道或者猜测到它们之间比较具体的关系,就可以尝试将他们转化为线性关系。简单举几个例子。
例如 1 y = a + b x \frac{1}{y}=a+\frac{b}{x} y1=a+xb,这并不是一个线性关系,但是我们令 y ′ = 1 y , x ′ = 1 x y'=\frac{1}{y},x'=\frac{1}{x} y′=y1,x′=x1,原函数就变成了 y ′ = a + b x ′ y'=a+bx' y′=a+bx′,妥妥的线性关系。再比如, y = a e b x y=ae^{bx} y=aebx,先取对数,得到 l n ( y ) = l n ( a ) + b x ln(y)=ln(a)+bx ln(y)=ln(a)+bx,令 y ′ = l n ( y ) , a ′ = l n ( a ) y'=ln(y),a'=ln(a) y′=ln(y),a′=ln(a),又化成了 y ′ = a ′ + b x y'=a'+bx y′=a′+bx的形式。再比如 y = 1 a + b e − x y=\frac{1}{a+be^ {-x}} y=a+be−x1,先两边取倒数,再进行一个变量转化,一样得到标准的线性关系。
当然啦,不是每一个非线性函数都可以转化为线性形式( y = a + b 1 x 1 + b 2 x 2 + . . . + b n x n y=a+b_1x_1+b_2x_2+...+b_nx_n y=a+b1x1+b2x2+...+bnxn)的形式。我们可以看到,线性形式下,如果把参数看成自变量,那函数相对于参数也是线性的。如果非线性函数相对于参数不是线性的,那就不太可能将其转化为线性函数。例如 y = a ( x − b ) 2 , y = a s i n ( b + c x ) y=a(x-b)^2,y=asin(b+cx) y=a(x−b)2,y=asin(b+cx)等等,这种时候,直接使用非线性拟合可能会更合适。
线性拟合的另一个问题是,需要先确定 x x x与 y y y这两组数据之间存在着一定的线性关系。如果数据之间的线性关系本就不强,即使可以用非线性转化为线性,拟合出来的效果也不会太好。因此,在进行线性关系拟合之前,一定要先通过作图,以及求解相关系数来确认它们确实具有线性关系,不然就凉凉了。嗯,一定要画散点图看一看啊。(写到这里想起来考试题中相关系数很大的数据点也可能不具备线性关系……然后我就答错了)
评价拟合效果
在拟合完成后,我们还想要知道我们找到的函数是否能很好的拟合我们的数据,这里引入了 S S T , S S R , S S E SST,SSR,SSE SST,SSR,SSE以及 R 2 R^2 R2的概念。其中 S S T = ∑ i = 1 n ( y i − y ˉ ) 2 SST=\sum_{i=1}^n(y_i-\bar{y})^2 SST=∑i=1n(yi−yˉ)2,称之为总体平方和,代表着实际的 y y y值相对于样本中心 y ˉ = 1 n ∑ i = 1 n y i \bar{y}=\frac{1}{n}\sum_{i=1}^ny_i yˉ=n1∑i=1nyi的波动程度, S S R = ∑ i = 1 n ( y i ^ − y ˉ ) 2 SSR=\sum_{i=1}^n(\hat{y_i}-\bar{y})^2 SSR=∑i=1n(yi^−yˉ)2,称之为回归平方和,代表着拟合的 y ^ \hat{y} y^值相对于样本中心 y ˉ = 1 n ∑ i = 1 n y i \bar{y}=\frac{1}{n}\sum_{i=1}^ny_i yˉ=n1∑i=1nyi的波动程度, S S E = ∑ i = 1 n ( y i ^ − y i ) 2 SSE=\sum_{i=1}^n(\hat{y_i}-y_i)^2 SSE=∑i=1n(yi^−yi)2,称之为误差平方和,代表着实际值与真实值的偏差程度,也是我们求解最小二乘时优化问题的目标函数。
之后,我们便可以引入拟合优度 R 2 R^2 R2的概念, R 2 = S S R S S T R^2=\frac{SSR}{SST} R2=SSTSSR,也就是说,拟合优度等于拟合结果的变动量在实际变动量之中的占比。嗯,是有一点儿玄,其实大概可以意会一下。给定了二维平面的一组点,假设其呈线性分布,那么它们在y轴上的中心是固定的,实际的y便相对于这个中心上下波动。而这个中心也刚好位于拟合直线上面,因此,我们使用拟合值距离这个中心的波动程度与实际值距离此中心的波动程度进行比较,用他们的比值来表示拟合的效果,倒也是可以理解的。同时,由于我们有一个最小化 S S E SSE SSE的目标,所以也避免了一些比较特殊的情况。例如实际值和理论值刚好关于中心点对称分布,虽然此时 R 2 R^2 R2达到了100%,但很明显拟合效果是极差的。
另外,对于线性拟合来说, S S T = S S R + S S E SST=SSR+SSE SST=SSR+SSE,所以 R 2 ∈ [ 0 , 1 ] R^2\in [0,1] R2∈[0,1],这个就自己证明吧。如果拟合函数不是线性函数,那上述的等式不一定成立,此时 R 2 R^2 R2的范围也无法约束在 [ 0 , 1 ] [0,1] [0,1]之间,再使用 R 2 R^2 R2对拟合效果进行评价,就不太合适了。这个时候,我们可以通过最小化 S S E SSE SSE,然后画画图,来看看实际的拟合效果了。
这里提供一下一元线性拟合的matlab代码。
clear;clc
x= [2.7000;2.9000;3.3000;3.5000;3.6000;3.8000;4.2000;5.5000;5.6000;5.9000;6.000;6.1000;6.6000;6.9000];
y= [4.2000;4.6000;6.0000;6.1000;6.6000;7.9000;8.4000;9.9000;10.3000;11.5000;11.7000;12.0000;13.2000;13.3000];
plot(x,y,'o')
% 给x和y轴加上标签
xlabel('x的值')
ylabel('y的值')
n = size(x,1);
k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))
hold on % 继续在之前的图形上来画图形
grid on % 显示网格线
% % 画出y=kx+b的函数图像 plot(x,y)
% % 传统的画法:模拟生成x和y的序列,比如要画出[0,5]上的图形
% xx = 2.5: 0.1 :7 % 间隔设置的越小画出来的图形越准确
% yy = k * xx + b % k和b都是已知值
% plot(xx,yy,'-')
% 匿名函数的基本用法。
% handle = @(arglist) anonymous_function
% 其中handle为调用匿名函数时使用的名字。
% arglist为匿名函数的输入参数,可以是一个,也可以是多个,用逗号分隔。
% anonymous_function为匿名函数的表达式。
% 举个小例子
% z=@(x,y) x^2+y^2;
% z(1,2)
% % ans = 5
% fplot函数可用于画出匿名一元函数的图形。
% fplot(f,xinterval) 将匿名函数f在指定区间xinterval绘图。xinterval = [xmin xmax] 表示定义域的范围
a=[x,y];
a=sort(a,1);
x1=a(:,1);
y1=a(:,2);
f=@(x) k*x+b;
fplot(f,[2.5,7]);
xx=2.7:0.01:7;
yy = interp1(x1,y1,xx,'linear');
hold on;
plot(xx,yy,"r");
legend('样本数据','拟合函数','插值函数','location','SouthEast')
y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2) % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR % 5.6843e-14 = 5.6843*10^-14 matlab浮点数计算的一个误差
R_2 = SSR / SST
matlab拟合工具箱
matlab提供了一个功能比较多的拟合工具箱Curve Fitting,好像需要安装来着,我也记不清了,如果没安装的话,在命令行输出“cftool”就会提示你进行安装,如果已经安装了就会调出工具箱的窗口。

cftool至多可以对三维数据进行拟合,默认状态下,数据来自于工作区中的变量。如上图所示,如果工作区中没有变量,直接设定 x , y , z x,y,z x,y,z是找不到数据的。因此我们可以先在工作区中导入数据。举个例子,首先运行一下代码导入三组变量。
clc;clear;
x= [2.7000;2.9000;3.3000;3.5000;3.6000;3.8000;4.2000;5.5000;5.6000;5.9000;6.000;6.1000;6.6000;6.9000];
y= [4.2000;4.6000;6.0000;6.1000;6.6000;7.9000;8.4000;9.9000;10.3000;11.5000;11.7000;12.0000;13.2000;13.3000];
x1=1:15;
y1=30*sin(2*x1+3)+5*rand;
x2=1:0.5:15;
y2=15*log(x2+5.5)+10+2*rand;
其中第一组数据是线性关系,有两个参数;第二组是三角函数关系,有三个参数;第三组是对数关系,有三个参数。接下来我们使用cftool看一看拟合的效果。


如图,当工作区有变量的时候,就可以在cftool中使用变量了。如果打开了右上角的 A u t o f i t Auto fit Autofit,导入变量之后就会呈现出拟合效果以及相应的一些指标。cftool提供了多种拟合方法,例如多项式拟合,指数拟合,傅里叶拟合等等,这个就自己研究啦。使用不同的拟合方法,在 r e s u l t result result框中会有不同的函数形式。当然,也支持自定义函数,如图。

可以发现,cftool的拟合效果还是比较强大的,大家可以多多尝试。
最后
最后,拟合有哪些作用呢?可以对函数进行逼近,进而用拟合出来的函数去预测未来的值。这种预测相对于插值的预测,特别是在已知数据区间之外的预测,要更为准确。相关原因之前简单提及了,更加专业的原因以及思考请自行查阅啦。此外,使用拟合对参数进行求解,可以用来解释一些实际问题,例如解释经济含义等等。不同的拟合函数形式也可以解决不同的问题,解释变量之间各种各样的相关关系。
拟合也存在着一个典型的问题,即过拟合现象。如果你的参数个数要比变量的个数还要多,那么在具体拟合的时候,很可能会得到很小的 S S E SSE SSE。单从拟合的角度而言是没问题的,但是这种过拟合,可能无法合理地解释实际问题,因此在拟合的时候需要注意过拟合的问题。其实插值,例如拉格朗日插值这种可以得到一个单一函数的插值方法,我们就可以将它理解为过拟合。虽然它的 S S E = 0 SSE=0 SSE=0,已经达到了最好,但无论是用来预测未来,还是用来解释现象,插值函数都不是一个很好的选择。所以呀,要注意过拟合的问题。
同时,本文基本上只涉及了一元函数的拟合问题。实际上一元线性拟合就是一元线性回归,多元线性拟合也可以看成多元线性回归,都是对参数进行求解,二者在操作上并没有太大区别。我认为他们的区别可能在于出发点不同,即回归的时候应该是已知函数形式的,而拟合的时候是不了解函数具体形式的。所以线性方面,拟合和回归应该是一个道理。至于多元非线性拟合,我认为在完全不了解函数形式的情况下,是很难完成的……可以想到的函数形式太多了。而如果通过理论、经验等手段知晓了函数的形式,那又变成了一个回归的问题,可以使用matlab的函数或者1stOpt这一软件求解,具体的之后再说吧……
嗯,以上就是关于拟合我想说的全部话题了,如有错误,欢迎指出。
就这样,拜拜~
对了对了,欢迎关注公众号“我是陈小白”~




