【TSP问题】基于Hopfield神经网络求解旅行商问题附Matlab代码
1 简介
本文给出了一种基于Hopfield神经网络模型求解TSP问题的算法.Hopfield网络是一种网状网络,网络中的每个神经元都可以和其他神经元双向连接.这种连接方式使得网络中每个神经元的输出都能反馈到同一层次的其他神经元,因此,它是一种反馈网络.根据网络节点的状态,Hopfield网络可分为离散的和连续的两种类型.离散的网络,其节点状态仅取 两个值;而连续的网络,其节点状态可以取区间 上任何值.Hopfield神经网络在联想记忆,组合优化和机器人控制等方面有重要的应用.其中Hopfield网络用于优化计算是最常见的.Hopfield网络的能量函数是一个多维神经元状态的标量函数,在网络收敛的稳定点上的能量函数最小.因此,设计网络权值W和输入,将优化问题中的目标函数,约束条件与能量函数联系起来,那么能量函数的极小点也是目标函数满足约束条件的极小点,所以Hopfield网络也可用于求解优化计算问题
2 部分代码
% 路径寻优作图function PlotR(V,citys)figure;citys_origin=citys;citys=[citys;citys(1,:)];[xxx,order]=max(V);New=citys(order,:);New=[New;New(1,:)];subplot(1,2,1)plot(citys(1,1),citys(1,2),'*') % first cityhold onplot(citys(2,1),citys(2,2),'+') % second cityhold onplot(citys(:,1),citys(:,2),'o-')for i=1:length(citys_origin)text(citys_origin(i,1),citys_origin(i,2),[' ' num2str(i)])endxlabel('X axis')ylabel('Y axis')title('Original Route')axis([0 1 0 1])grid onsubplot(1,2,2)plot(New(1,1),New(1,2),'*') % first cityhold onplot(New(2,1),New(2,2),'+') % second cityhold onplot(New(:,1),New(:,2),'o-')for i=1:length(citys_origin)text(citys_origin(i,1),citys_origin(i,2),[' ' num2str(i)])endxlabel('X axis')ylabel('Y axis')title('TSP solution')axis([0 1 0 1])axis ongrid on
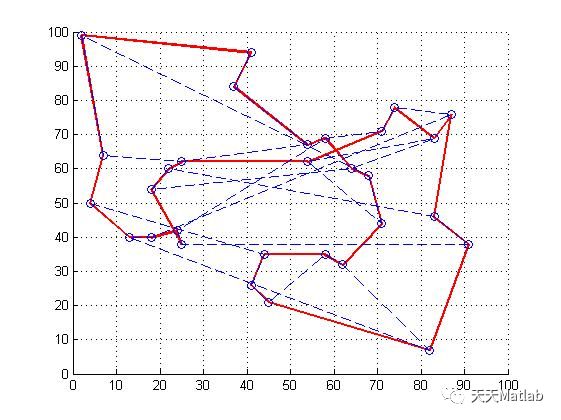
3 仿真结果
4 参考文献
[1]于慧, 徐慧. 基于Hopfield神经网络模型求解TSP问题的算法[J]. 2008.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。