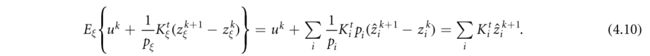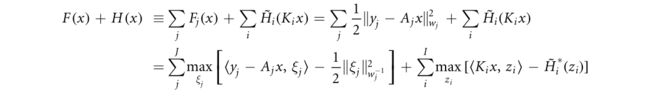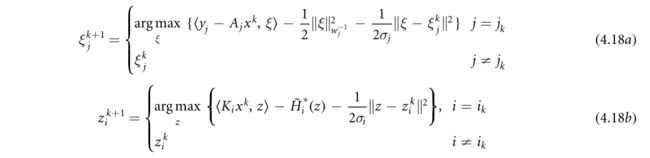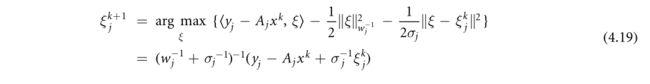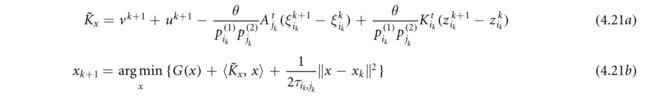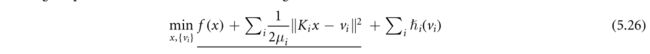文献翻译__人工智能时代医学图像重建中的凸优化算法(第4、5、6章)
文章下载–我的Gitee
Convex optimization algorithms in medical image reconstruction—in the age of AI
人工智能时代医学图像重建中的凸优化算法
人工智能时代医学图像重建中的凸优化算法
- 文章下载--我的Gitee
- Convex optimization algorithms in medical image reconstruction—in the age of AI
- 人工智能时代医学图像重建中的凸优化算法
-
- 4.凸优化的随机一阶算法
-
- 4.1.随机方差缩减梯度算法
- 4.2.方差减少的加速梯度
- 4.3.原始对偶随机梯度
- 4.4.其他随机算法
- 4.5.应用程序
- 4.6.讨论
- 5.非凸优化中的凸性
-
- 5.1.基本定义
- 5.2.具有弱凸正则项的凸优化
- 5.3.基于模型的非凸优化
-
- 5.3.1.类型1:ϕ=f+h,f非凸光滑的,h简单,K=I
- 5.3.2.类型2:ϕ=fx) +hK ),f非凸光滑的,h简单的
- 5.4.讨论
- 6.凸性、图像重建和DL的协同集成
-
- 6.1.在MBIR管道中嵌入CNN
- 6.2.在DL流水线中嵌入凸优化层
- 6.3.讨论
- 7.结论
4.凸优化的随机一阶算法
随机算法在机器学习中有着悠久的历史,可以追溯到20世纪50年代的经典随机梯度下降算法(Robbins和Monro 1951)。研究随机算法有“直观的、实用的和理论的动机”(Bottou等人,2018年)。直观地说,如果许多训练样本在统计上是同类的,随机算法可以比它们的确定性对应算法更有效(Bertsekas 1999),在某种意义上,在第110页。这一直觉在实践中得到了证实:随机算法通常具有快速的初始训练误差减少,比确定性/批处理算法快得多。最后,建立了随机算法的收敛理论,以支持实际结果。如今,深度神经网络完全是用随机算法训练的,重申了它们的有效性和实用价值。
有序子集(OS)算法在图像重建中很流行,就像随机算法在机器学习中很流行一样。自1994年Hudson和Larkin用于核医学图像重建以来,由于不断增加的数据量和对及时交付满意图像的高要求,OS算法继续蓬勃发展。OS算法通常将投影视图划分为组,并在循环遍历每个组后执行图像更新。尽管这些OS算法中可能没有随机元素,但在使用数据子集(小批量)进行更频繁的参数更新方面,它们在本质上与随机算法非常相似。因此,OS算法通常具有快速的初始进展,这可能导致以其批处理对应的计算成本的一小部分来获得可接受的图像质量。然而,由于缺乏对算法行为的一般理解,OS算法经常因达到极限环或发散而受到批评。OS算法可能实质上受益于凸优化的随机算法,特别是后者通常具有收敛保证的事实。
在文献中,术语‘随机算法’可以是模棱两可的,因为它可以指:
(a)用于最小化随机目标函数的算法,例如,在期望风险最小化中;
(b)基于返回扰动函数值或梯度信息的随机预言的算法
©用于确定性有限和最小化的算法,例如,经验风险最小化,其中随机机制仅产生于对目标函数中的组件的子集(小批量)的随机访问。
由于我们的主要兴趣是解决具有确定性有限和目标函数的图像重建问题,因此我们主要关注第三类随机算法。在文献中,它们有时也被称为随机化算法。对于确定性有限和最小化,随机性是可选的,而不是强制性的,并且该选项可以有效地利用其计算优势。
机器学习中的一个常见问题是下面的正则化经验风险最小化问题:
min x ϕ ( x ) = f ( x ) + g ( x ) , f ( x ) = 1 n ∑ i = 1 n f i ( x ) (4.1) \min_x \phi(x)=f(x)+g(x),f(x)=\frac{1}{n}\sum_{i=1}^nf_i(x)\tag{4.1} xminϕ(x)=f(x)+g(x),f(x)=n1i=1∑nfi(x)(4.1)
其中 f i ( x ) , i = 1 , . . . , n f_i(x),i=1,...,n fi(x),i=1,...,n,是CCP, L i L_i Li-光滑,正则化g(x)是CCP,非光滑,简单。我们假设 x ∗ ∈ a r g m i n ϕ ( x ) x_*\in argmin\phi(x) x∗∈argminϕ(x)存在。
经典的随机梯度下降(SGD)算法假定g(x)=0,并使用f(x)估计解x*。
x k + 1 = x k − η ▽ f i k ( x k ) (4.2) x_{k+1}=x_k-\eta \triangledown f_{i_k}(x_k)\tag{4.2} xk+1=xk−η▽fik(xk)(4.2)
其中 i k i_k ik从 1 , . . . , n {1,...,n} 1,...,n中随机抽取, η k > 0 η_k>0 ηk>0是步长。处理复合目标函数(4.1)的自然概括是(4.2)的以下近端变体(肖2010,Dekel等人2012):
x k + 1 : = a r g min x { g ( x ) + f ( x k ) + < ▽ f i k ( x k ) , x − x k > + 1 2 η k ∣ ∣ x − x k ∣ ∣ 2 } (4.3) x_{k+1}:=arg\min_x \{g(x)+f(x_k)+<\triangledown f_{i_k}(x_k),x-x_{k}>+\frac1{2\eta_k}||x-x_k||^2\}\tag{4.3} xk+1:=argxmin{g(x)+f(xk)+<▽fik(xk),x−xk>+2ηk1∣∣x−xk∣∣2}(4.3)
当g(x不存在时,(4.3)等同于(4.2);当g(x)存在时,(4.3)是(4.2)的近端梯度变量。在(4.2)和(4.3)中, ∇ f i k ( x k ) {\rm{\nabla }}{f}_{{i}_{k}}({x}_{k}) ∇fik(xk)可视为真梯度 ∇ f ( x k ) = ∑ i ∇ f i ( x k ) / n ∇f(x_k)=∑_i∇f_i(x_k)/n ∇f(xk)=∑i∇fi(xk)/n的估计.显然, E ξ { ∇ f ξ ( x k ) } = ∇ f ( x k ) E_ξ\{∇f_ξ(x_k)\}=∇f(x_k) Eξ{∇fξ(xk)}=∇f(xk), 18 ^{18} 18因此 ∇ f ξ ( x k ) ∇f_ξ(x_k) ∇fξ(xk)是一个无偏估计;而且,计算一个分量函数的 ∇ f i ( x k ) ∇f_i(x_k) ∇fi(xk)比计算全梯度 ∇ f ( x k ) ∇f(x_k) ∇f(xk)简单n倍.。如果我们假设 ∥ ∇ f i ( x ) ∥ 2 < = M ∥∇f_i(x)∥^2<=M ∥∇fi(x)∥2<=M对所有i,对所有x,则可以证明 E ξ { ∥ ∇ f ξ ( x k ) − ∇ f ( x k ) ∥ 2 } < = M E_ξ\{∥∇f_ξ(x_k)−∇f(x_k)∥^2\}<=M Eξ{∥∇fξ(xk)−∇f(xk)∥2}<=M(Konečnèet al2015),即 ∇ f ξ ( x k ) ∇f_ξ(x_k) ∇fξ(xk),作为 ∇ f ( x k ) ∇f(x_k) ∇f(xk)的估计,有有限的方差。在步长 η k = η η_k=η ηk=η不变的情况下,梯度估计的有限方差导致期望目标值 19 ^{19} 19的有限误差界,即 E f ( x k ) − f ( x ∗ ) → B {E}f({x}_{k})-f({x}_{* })\to B Ef(xk)−f(x∗)→B为 k → ∞ k→∞ k→∞。误差界B取决于步长η和梯度方差:η越小,B越小,M越小。
由于梯度估计的方差M有限,SGD(4.2)、(4.3)的收敛通常需要减小步长。在f(x)是L-光滑且μ-强凸的假设下,(4.3)用递减步长 η k ∼ 1 / k η_k∼1/k ηk∼1/k以O(M/k)的速度收敛于 E ϕ ( x k ) → ϕ ( x ∗ ) {\mathbb{E}}\phi ({x}_{k})\to \phi ({x}_{* }) Eϕ(xk)→ϕ(x∗),当分支f(x)仅是L光滑时,收敛速度(由 E ϕ ( x ˉ k ) → ϕ ( x ∗ ) {\mathbb{E}}\phi ({\bar{x}}_{k})\to \phi ({x}_{* }) Eϕ(xˉk)→ϕ(x∗)来度量,其中 x ˉ k = ∑ i k x i / k {\bar{x}}_{k}={\sum }_{i}^{k}{x}_{i}/k xˉk=∑ikxi/k用步长规则 η k ∼ 1 / k {\eta }_{k}\sim 1/\sqrt{k} ηk∼1/k减小到 O ( M / k ) { \mathcal O }(M/\sqrt{k}) O(M/k)。
减小梯度方差M并由此改进收敛的一种方式是用小批量梯度估计器 ∇ f i k ( x k ) {\rm{\nabla }}{f}_{{i}_{k}}({x}_{k}) ∇fik(xk)代替单分量梯度估计器 ∇ ~ b f ( x k ) = 1 b ∑ i ∈ S ∇ f i ( x k ) {\tilde{{\rm{\nabla }}}}_{b}f({x}_{k})=\tfrac{1}{b}{\sum }_{i\in S}{\rm{\nabla }}{f}_{i}({x}_{k}) ∇~bf(xk)=b1∑i∈S∇fi(xk),其中S是随机均匀地抽取的基数b的 1 , . . . , n {1,...,n} 1,...,n的子集。显然,小批量梯度估计 ∇ ~ b f ( x k ) {\tilde{{\rm{\nabla }}}}_{b}f({x}_{k}) ∇~bf(xk)仍然是无偏的。关于它的方差,可以证 E S ∥ ∇ ~ b f ( x k ) − ∇ f ( x k ) ∥ 2 ⩽ ( n − b ) / ( b ( n − 1 ) ) M {E}_{{\rm{S}}}\parallel {\tilde{{\rm{\nabla }}}}_{b}f({x}_{k})-{\rm{\nabla }}f({x}_{k}){\parallel }^{2}\leqslant (n-b)/(b(n-1))M ES∥∇~bf(xk)−∇f(xk)∥2⩽(n−b)/(b(n−1))M(Konečnèet al2015),其中条件期望是关于随机子集的。当b=n时,梯度方差约为M/b:小批量b越大,方差越小。有了小批量梯度估计器,每次迭代的成本也增加了系数b。因此,单样本SGD和小批量变量达到“精度”解决方案所需的总工作量是相当的(Bottou等人,2018年)。
可以推广简单的SGD算法(4.3),并用Bregman散度取代二次距离,如(Nomerovski等人,2009,Duchi等人,2010)中所考虑的那样。收敛速度和收敛速度基本保持不变,即在强凸性的O(1/k)或不强凸性的O( 1 / k 1/\sqrt{k} 1/k)(Juditsky等人2011)。这些速率落后于确定性对应的速率,它们分别是 O ( α k ) O(α^k) O(αk)、0<α<1和O(1/k),后者可以用Nester ovʼ的方法进一步加速以获得最优速率。尽管收敛速度较慢,但正如我们稍后讨论的那样,对于一些低精度解决方案就足够的大规模机器学习应用来说,SGD可能仍然比它们的批处理对应物更可取。
正如我们已经提到的,随机算法的主要计算吸引力在于每次迭代的低成本。算法复杂性的公平比较应该是对总工作量的某种度量,该度量既考虑了每次迭代的成本,也考虑了迭代的收敛速度依赖性。对于目标函数(4.1),总工作量可以通过访问(分量)函数值或梯度评估的总次数以及正则化函数g的近似值映射来确定。表1列出了根据目标函数(4.1)中的分量函数的性质总结的,对于确定性和随机性算法而言,达到“次优解”所需的总工作量。
- 类型I: ▽ f i k ( x k ) \triangledown f_{i_k}(x_k) ▽fik(xk)是Li光滑的,g(x)是非平滑的并且是μ强凸的
- 类型II: ▽ f i k ( x k ) \triangledown f_{i_k}(x_k) ▽fik(xk)是Li光滑的,g(x)是非光滑和非强凸的
- 类型III: ▽ f i k ( x k ) \triangledown f_{i_k}(x_k) ▽fik(xk)是非平滑的, L i L_i Li-Lipschitz,g(x)是非强凸的;
表1.样本算法的总工作量和为不同类型的问题得出“次优解”的下限,改编自(Woodworth和Srebro 2016)。
我们以AGD为例来说明如何阅读表格。从第3.2.2节开始,第二类问题的AGD的收敛速度是 O ( L k 2 ) { \mathcal O }\left(\tfrac{L}{{k}^{2}}\right) O(k2L)。然后,为了得到一个次优解,我们大致需要 K = L ϵ K=\sqrt{\tfrac{L}{\epsilon }} K=ϵL迭代。全梯度法的每次迭代成本为n-乘以随机梯度法,总工作量为 n L ϵ n\sqrt{\tfrac{L}{\epsilon }} nϵL。表中的其他项目一以类似的方式计算。
如果我们比较GD和SGD在最小化第二类问题上的总工作量,当 n > L ϵ n>{\tfrac{L}{\epsilon }} n>ϵL时,当训练样本n较大且精度要求较低时,SGD在计算上比GD更有吸引力。这证明了随机方法在许多大规模机器学习任务中的受欢迎程度,即使它们的理论收敛速度落后于确定性方法。
如表1所示,在确定性算法的复杂性中有一个始终存在的因素n。对于随机算法,此因素取决于算法。为了正确地衡量随机算法的(次)最优性,一些研究(Lan 2012,Woodworth和Srebro 2016)研究了使用一阶随机方法求解(4.1)的低复杂性界,这些方法也包括在表1中。一个有趣的观察是,随机算法比它们的确定性算法具有更小的低复杂性界,就n对数据样本数量的依赖性而言。在比较随机算法和确定性算法时,一个微妙之处在于,与确定性算法不同,随机算法的收敛通常是用期望来衡量的。相比之下,确定性算法的收敛速度是针对最坏情况的。
早期的SGD方法(4.3)在有偏梯度估计的情况下,对梯度估计只需很少的假设,即有限方差或有限均方误差(MSE)。这一方面使它们成为诸如预期风险最小化甚至在线最小化等问题的理想选择;同时,当它们应用于具有确定性、有限和目标(4.1)的问题时,这种一般性性质是更快收敛的瓶颈,其中如果需要的话,完全梯度是可用的。
4.1.随机方差缩减梯度算法
许多减少方差的技术,例如见(Konečny`和Richtárik 2013,Defazio等人2014,Schmidt等人2017),已经被提出来改善解决(4.1)的梯度估计器。然后将这些技术与SGD结合起来以提高收敛性。其中一些技术,例如SAGA(Defazio等人,2014)和SAG(Schmidt等人,2017),需要存储所有过去的n个梯度信息,这对于图像重建来说可能是内存不足的。我们对内存高效的方差减少技术更感兴趣。其中一个例子是SVRG(Johnson和Zhang 2013)及其扩展Prox-SVRG,用于解决(4.1),如算法4.1所示。
| 算法4.1 Prox-SVRG算法求解(4.1) |
|---|
| 输入:步长 η η η,内部迭代# m = 2 n m=2n m=2n,初始值 x ˉ 0 {\bar{x}}_{0} xˉ0。 |
| 输出: x ˉ S {\bar{x}}_{S} xˉS |
| 1 for s = 0,…,K-1 do |
| 2 v ˉ 0 = ∇ f ( x ˉ s ) , x 0 = x ˉ s \bar{v}_0={\rm{\nabla }}f({\bar{x}}_{s}),x_0={\bar{x}}_{s} vˉ0=∇f(xˉs),x0=xˉs |
| 3 for k = 0,…,m-1 do |
| 4 随机选择 i k ∈ { 1 , . . . , n } i_k\in \{1,...,n\} ik∈{1,...,n},这样 P r o b ( i k = i ) = p Prob(i_k=i)=p Prob(ik=i)=p |
| 5 v k : = v ˉ 0 + 1 p i k n [ ∇ f i k ( x k ) − ∇ f i k ( x ˉ s ) ] {v}_{k}:= \bar{v}_0+\tfrac{1}{{p}_{{i}_{k}}n}\left[{\rm{\nabla }}{f}_{{i}_{k}}({x}_{k})-{\rm{\nabla }}{f}_{{i}_{k}}({\bar{x}}_{s})\right] vk:=vˉ0+pikn1[∇fik(xk)−∇fik(xˉs)] /variance reduction/ |
| 6 x k + 1 : = arg m i n x { g ( x ) + ⟨ v k , x ⟩ + 1 2 η ∥ x − x k ∥ 2 } {x}_{k+1}:= {\arg min}_{x}\{g(x)+ \langle {v}_{k},x \rangle +{\frac{1}{2\eta}}\parallel x-{x}_{k}{\parallel }^{2}\} xk+1:=argminx{g(x)+⟨vk,x⟩+2η1∥x−xk∥2} /proximal gradient descent/ |
| 7 x ˉ s + 1 : = ∑ i = 1 m x i / m {\bar{x}}_{s+1}:= {\sum }_{i=1}^{m}{x}_{i}/m xˉs+1:=∑i=1mxi/m |
这个算法有一个内-外循环结构。在每次外迭代中,都会计算一个完整的梯度 v ˉ 0 {\bar{v}}_{0} vˉ0(第2行),随后用于 "锚定 "接下来的m个内迭代的随机梯度 v k v_k vk(第5行)。实际的参数更新是在第6行进行的,这与(4.3)类似, v k v_k vk是梯度估计。很容易看出梯度估计 v k v_k vk是无偏的,因为 E ( v k ) = ∇ f ( x k ) E(v_k)=∇f(x_k) E(vk)=∇f(xk);此外,有研究表明(Johnson和Zhang 2013,Xiao和Zhang 2014),梯度估计的方差可以被候选解 x k , x ˉ s x_k,{\bar{x}}_{s} xk,xˉs的次优性所限制。更具体地说。
E { ∣ ∣ v k − ∇ f ( x k ) ∣ ∣ 2 } < = C ( ϕ ( x k ) − ϕ ( x ∗ ) + ϕ ( x ˉ s ) − ϕ ( x ∗ ) ) (4.4) E\{||v_k-\nabla f(x_k)||^2\}<=C(\phi(x_k)-\phi(x_*)+\phi(\bar{x}_s)-\phi(x_*))\tag{4.4} E{∣∣vk−∇f(xk)∣∣2}<=C(ϕ(xk)−ϕ(x∗)+ϕ(xˉs)−ϕ(x∗))(4.4)
(4.4)中的常数C与分量函数 f i f_i fi的梯度Lipschitz常数和采样方案有关。从(4.4)中可以看出,算法的收敛性意味着梯度方差确实趋于0,因此被称为方差减小。对于I型问题,Prox-SVRG实现了线性收敛(Xiao和Zhang 2014),即 E { ϕ ( x ˉ s ) − ϕ ( x ∗ ) } → ρ s {\mathbb{E}}\{\phi ({\bar{x}}_{s})-\phi ({x}_{* })\}\to {\rho }^{s} E{ϕ(xˉs)−ϕ(x∗)}→ρs,其中几何系数0 其中几何系数0 < ρ < 1取决于问题参数,如梯度Lipschitz常数、强凸性参数和内部迭代次数m;对于第二类问题,(Prox-)SVRG实现了亚线性收敛O (1/k)。
与SGD相比,Prox-SVRG在提高收敛速度的同时增加了计算量和内存开销。SGD每次迭代计算一个梯度;Prox-SVRG每次迭代总共有2m + n个梯度计算,发生在第5行(2m)和第2行(n)。Prox-SVRG还需要存储两个额外的变量 v ˉ 0 \bar{v}_0 vˉ0和 x ˉ 0 {\bar{x}}_{0} xˉ0,即两倍的内存。对于典型的图像重建问题,这两种成本都是可控的。与I类问题的简单GD相比,在总工作方面的计算节省来自于对于典型问题设置的 n + L μ ≪ n L μ n+\tfrac{L}{\mu }\ll n\tfrac{L}{\mu } n+μL≪nμL(参见表1)。
对于无偏梯度估计器和有偏梯度估计器,均可进行减方差。除了(PROX-)SVRG外,使用VR的其他无偏梯度估计包括SAGA(DeFazio等人,2014年)和S2GD(Konečný和Richtárik,2013年)。另一方面,SAG(Schmidt Et Al 2017)和Sarah(Nguyen Et Al 2017)是实现VR的有偏估计者。Sarah的一个版本相当于将算法4.1的第5行替换为以下内容:
v k = v k − 1 + 1 p i k n [ ∇ f i k ( x k ) − ∇ f i k ( x k − 1 ) ] , v 0 = v ˉ 0 (4.5) v_k=v_{k-1}+\frac1{p_{i_k}n}[\nabla f_{i_k}(x_{k})-\nabla f_{i_k}(x_{k-1})],v_0=\bar{v}_0\tag{4.5} vk=vk−1+pikn1[∇fik(xk)−∇fik(xk−1)],v0=vˉ0(4.5)
梯度估计器(4.5)通过利用 v k v_k vk和 x k x_k xk的最新更新递归地建立梯度信息,而不像SVRG在内循环开始时重复使用该值。一个直接的观察是, v k v_k vk是有偏梯度估计,即 E ( v k ) = ∇ f ( x k ) − ∇ f ( x k − 1 ) − v k − 1 E(v_k)=∇f(x_k)-∇f(x_{k-1})-v_{k-1} E(vk)=∇f(xk)−∇f(xk−1)−vk−1.然而,对于类似于(Prox-)SVRG的第I类问题,SALA线性收敛被证明。
20个这样的结果是用还原技术得到的。有关更多详细信息,请参阅第4.6节。
4.2.方差减少的加速梯度
降方差SGD方法能够达到传统确定性算法的收敛速度。在过去的十年中,确定性凸优化算法得到了迅速的发展:由于Nester ovʼ的动量技术,最先进的确定性算法现在可以达到最优的收敛速度。一个自然的问题是,方差减少的随机算法是否可以直接受益于动量技术。这一问题首先由Katyusha(Allen-朱,2017)作了肯定的回答。
| 算法4.2 Katyushans解(4.1)。 |
|---|
| 输入:内部迭代# m = 2 n , τ 3 = 1 / 2 m=2n,\tau_3=1/2 m=2n,τ3=1/2,初始值 x ˉ 0 {\bar{x}}_{0} xˉ0。 |
| 输出: x ˉ S {\bar{x}}_{S} xˉS |
| 1 for s = 0,…,S-1 do |
| 2 τ 1 , s = 2 s + 4 {\tau }_{1,s}=\tfrac{2}{s+4} τ1,s=s+42 |
| 3 v ˉ 0 = ∇ f ( x ˉ s ) \bar{v}_0={\rm{\nabla }}f({\bar{x}}_{s}) vˉ0=∇f(xˉs) |
| 4 for k = 0,…,m-1 do |
| 5 y k = τ 1 , s z k + τ 2 x ˉ s + ( 1 − τ 1 , s − τ 2 ) x k {y}_{k}={\tau }_{1,s}{z}_{k}+{\tau }_{2}{\bar{x}}_{s}+(1-{\tau }_{1,s}-{\tau }_{2}){x}_{k} yk=τ1,szk+τ2xˉs+(1−τ1,s−τ2)xk /Nesterovʼs momentum + ‘negative’ momentum/ |
| 6 随机选择 i k ∈ { 1 , . . . , n } i_k\in \{1,...,n\} ik∈{1,...,n},这样 P r o b ( i k = i ) = p i = 1 / n Prob(i_k=i)=p_i=1/n Prob(ik=i)=pi=1/n |
| 7 v k : = v ˉ + 1 p i k n [ ∇ f i k ( y k ) − ∇ f i k ( x ˉ s ) ] {v}_{k}:= \bar{v}+\tfrac{1}{{p}_{{i}_{k}}n}\left[{\rm{\nabla }}{f}_{{i}_{k}}({y}_{k})-{\rm{\nabla }}{f}_{{i}_{k}}({\bar{x}}_{s})\right] vk:=vˉ+pikn1[∇fik(yk)−∇fik(xˉs)] |
| 8 z k + 1 : = arg m i n x { g ( x ) + ⟨ v k , x ⟩ + 3 τ 1 , s L 2 ∥ x − z k ∥ 2 } {z}_{k+1}:= {\arg min}_{x}\{g(x)+ \langle {v}_{k},x \rangle +{\textstyle \tfrac{3{{\tau }}_{1,s}L}{2}}\parallel x-{z}_{k}{\parallel }^{2}\} zk+1:=argminx{g(x)+⟨vk,x⟩+23τ1,sL∥x−zk∥2} |
| 9 x k + 1 = τ 1 , s z k + 1 + τ 2 x ˉ s + ( 1 − τ 1 , s − τ 2 ) x k {x}_{k+1}={\tau }_{1,s}{z}_{k+1}+{\tau }_{2}{\bar{x}}_{s}+(1-{\tau }_{1,s}-{\tau }_{2}){x}_{k} xk+1=τ1,szk+1+τ2xˉs+(1−τ1,s−τ2)xk |
| 10 x ˉ s + 1 : = ∑ i = 1 m x i / m {\bar{x}}_{s+1}:= {\sum }_{i=1}^{m}{x}_{i}/m xˉs+1:=∑i=1mxi/m |
对于第一类和第二类问题,Katyusha不同的版本。算法4.2显示了第二类问题的Katyushans,其中上标‘ns’代表非强凸。就结构而言,Katyusha就像是Prox-SVRG和算法3.5的组合,后者是我们在第3.2.2节中讨论的Nester ovʼ加速方法的变体。Katyusha继承了Prox-SVRG的内外环结构和方差减少的梯度估计器。实际上,当设置参数 τ 1 , s = 1 τ_{1,s}=1 τ1,s=1和 τ 2 = 0 τ_2=0 τ2=0时,算法4.2与ProxSVRG4.2几乎相同(除了步长η)。同时,Katyusha使用Nestrovʼs的多步加速技术来生成序列( y k . z k + 1 , x k + 1 y_k.z_{k+1},x_{k+1} yk.zk+1,xk+1)(第5、8、9行)。Katyusha的一个显著特点是,有一个固定的权重 τ 2 τ_2 τ2分配给变量 x ˉ s {\bar{x}}_{s} xˉs,在该变量的外部循环中计算精确的梯度(第5,9行)。在较高的水平上,这种所谓的“负动量”是为了确保在Nester ovʼ的动量加速生效时,梯度估计不会偏离太远。建立了 x ˉ s {\bar{x}}_{s} xˉs的期望目标值的收敛和收敛速度,见表1。
请注意,从表1中可以看出,Katyusha ns的比率由 n / ϵ n/\sqrt{\epsilon } n/ϵ主导,其样本大小依赖性n高于随机算法的较低复杂度边界n,这使得它不比AGD更有利。继Katyusha之后,许多其他人,例如(Shang等人2017,Zhou等人2018,Lan等人2019,Zhou等人2019,Song等人2020),已经证明了加速的收敛速度,其中一些更接近于较低的复杂度界限。这些算法总是使用内外环结构,并使用在每次外部迭代中在锚点 x ˉ s {\bar{x}}_{s} xˉs处计算的全梯度来稳定梯度估计。因此,动量技术是否适用于其他不涉及“锚”的方差减少随机梯度算法(如SAGA和SARAH)会产生一个问题。
最近Driggs等人(Driggs Et Al 2020)回答了这个问题,它表明‘锚点’不是实现加速收敛速度所必需的。引入了另一个性质MSEB,以确保随着迭代k的继续,梯度估计量的均方误差和偏差都能足够快地减小;所有MSEB梯度估计量,包括SVRG、SAGA、Sarah等,都证明了加速收敛。因此,开发了一个更统一的加速框架。以算法3.5为模板,我们可以用任意的∇梯度估计 ∇ f ( y k ) {{\rm{\nabla }}}f({y}_{k}) ∇f(yk)代替精确的梯度估计 ∇ ~ f ( y k ) \tilde{{\rm{\nabla }}}f({y}_{k}) ∇~f(yk),从而建立加速收敛。
4.3.原始对偶随机梯度
经典的SGD算法用扰动的梯度代替精确的梯度,例如来自随机预言的梯度。以类似的方式,随机原始-对偶算法用它们的随机估计来代替原始变量和对偶变量的精确梯度。再次考虑我们的问题模型(3.1),经典的随机原始对偶算法(Nmirovski等人2009,Chen等人2014)具有以下形式:
z k + 1 : = a r g min z { < K ~ z ( x k ) , z > − h ∗ ( z ) + 1 2 σ k D 2 ( z , z k ) } x k + 1 : = a r g min x { g ( x ) + < x , K ~ x ( x k + 1 ) > + 1 2 τ k D 1 ( x , x k ) } (4.6) {z}^{k+1}:= arg \min_{z}\{<\tilde K_z(x^k),z>-h^*(z)+{\frac{1}{2\sigma_k}}D_2(z,z^k)\}\\\tag{4.6} {x}^{k+1}:= arg \min_{x}\{g(x)+
其中,(3.5中)中的精确梯度 K x Kx Kx和 K t z K^tz Ktz被它们的估计 K ~ z ( x k ) \tilde K_z(x^k) K~z(xk), K ~ x ( x k + 1 ) \tilde K_x(x^{k+1}) K~x(xk+1)所代替。在梯度估计的有限均方误差假设下,(4.6)以步长参数递减的速率 1 / k 1/\sqrt{k} 1/k收敛到 τ k , σ k ∼ 1 k {\tau }_{k},{\sigma }_{k}\sim \tfrac{1}{\sqrt{k}} τk,σk∼k1(Nymrovski等人,2009)。
与随机原始算法中的减方差方法类似,通过考虑模型问题的确定性、有限和性质,可以大大提高 1 / k 1/\sqrt{k} 1/k的收敛速度。对于机器学习和图像重建,目标中的复合函数 h ( K ⋅ ) h(K·) h(K⋅)通常可以分解如下:
min x g ( x ) + h ( K x ) , w h e r e h ( K x ) = ∑ i = 1 n h i ( K i x ) (4.7) \min_xg(x)+h(Kx),where h(Kx)=\sum_{i=1}^nh_i(K_ix)\tag{4.7} xming(x)+h(Kx),whereh(Kx)=i=1∑nhi(Kix)(4.7)
其中 h i h_i hi是CCP, k i , i = 1 , . . . , n k_i,i=1,...,n ki,i=1,...,n是线性算子 K i : R d → R m i , m = ∑ i n m i {K}_{i}:{R}^{d}\to {R}^{{m}_{i}},m=\sum_i^nm_i Ki:Rd→Rmi,m=∑inmi,对于机器学习,目标的有限和部分通常指的是n个训练样本的平均训练损失。在这种情况下,对于(4.7)中的h(Kx)的定义,总是有1/n的系数。对于图像重建,有限和主要来自数据保真项或正则化。在(4.7)中,我们坚持图像重建的约定,而不引入人工1/n缩放。这将需要对我们随后引入的面向机器学习的算法进行一些微小的改变。我们将在继续进行时指出这种适应。
通过利用 h i h_i hi的共轭函数 h i ∗ h_i^* hi∗,原始问题(4.7)引出以下原始-对偶问题:
min x max z i ∑ i = 1 n [ < K i ~ x , z i > − h i ∗ ( z i ) + g ( x ) ] (4.8) \min_x\max_{z_i}\sum_{i=1}^n[<\tilde{K_i}x,z_i>-h_i^*(z_i)+g(x)]\tag{4.8} xminzimaxi=1∑n[<Ki~x,zi>−hi∗(zi)+g(x)](4.8)
其中 z i ∈ R m i , i = 1 , . . . , n {z}_{i}\in {R}^{{m}_{i}},i=1,...,n zi∈Rmi,i=1,...,n是对偶变量。请注意,对偶变量 z i z_i zi在(4.8)中是完全可分离的。
下面的随机原始对偶坐标(SPDC)下降算法,改编自(Zhang和肖2017,Lan和周2018),用于我们的问题模型(4.7) 21 ^{21} 21,可以被视为简单确定性PDHG算法(3.5)的随机扩展。
对于迭代 k = 1 , . . . , k=1,..., k=1,...,从 1 , . . . , n {1,...,n} 1,...,n中随机抽取 i k i_k ik,使得 p r o b ( i k = i ) = p i prob(i_k=i)=p_i prob(ik=i)=pi。请按以下步骤操作:
z k + 1 : = { a r g min z { < K ~ i ( x k ) , z > − h ∗ ( z ) − 1 2 σ k ∣ ∣ z − z i k ∣ ∣ 2 } i = i k z i k i ≠ i k ∣ K ~ x = u k + 1 p i k K i k t ( z i k k + 1 − z i k k ) x k + 1 : = a r g min x { g ( x ) + < x , K ~ x ( x k + 1 ) > + 1 2 τ i k ∣ ∣ x − x k ∣ ∣ 2 } u k + 1 = u k + K i k t ( z i k k + 1 − z i k k ) x ˉ k + 1 = x k + 1 + θ ( x k + 1 − x k ) (4.9) {z}^{k+1}:= \left \{ \begin{array}{rcl} arg \min_{z}\{<\tilde K_i(x^k),z>-h^*(z)-{\frac{1}{2\sigma_k}}||z-z_i^k||^2\} & i=i_k\\ z_i^k & i \neq i_k \end{array}\right|\tag{4.9}\\ \tilde K_x=u^k+\frac1{p_{i_k}}K_{i_k}^{t}(z_{i_k}^{k+1}-z_{i_k}^{k})\\ {x}^{k+1}:= arg \min_{x}\{g(x)+
SPDC维护(3.5)的算法结构,并在双重(4.9a)和原始(4.9c)更新步骤中进行重要更改。我们首先注意到双重更新(4.9a)对应于双重变量{ z i z_i zi}的随机坐标上升。令 z ^ i k + 1 \widehat z_i^{k+1} z ik+1为并行完成的所有i的最大值(4.9a),即。
z ^ i k + 1 = a r g max z { < K ~ i ( x k ) , z > − h i ∗ ( z ) − 1 2 σ i ∣ ∣ z − z i k ∣ ∣ 2 } 任意 i ( ) \widehat z_i^{k+1}=arg\max_z\{<\tilde K_i(x^k),z>-h_i^*(z)-{\frac{1}{2\sigma_i}}||z-z_i^k||^2\} 任意i\tag{} z ik+1=argzmax{<K~i(xk),z>−hi∗(z)−2σi1∣∣z−zik∣∣2}任意i()
来自(4.9a)我们有:
z i k + 1 = { z ^ i k + 1 w i t h p r o b a b i l i t y p i z i k w i t h p r o b a b i l i t y 1 − p i ∣ ( ) z_i^{k+1}=\left \{ \begin{array}{rcl} \widehat z_i^{k+1}&with probability&p_i\\ z_i^k&with probability&1-p_i \end{array}\right|\tag{} zik+1={z ik+1zikwithprobabilitywithprobabilitypi1−pi∣ ∣()
如果算法被初始化为 u 0 = ∑ i K i t z i 0 {u}_{0}={\sum }_{i}{K}_{i}^{t}{z}_{i}^{0} u0=∑iKitzi0,则通过(4.9d),对于所有的k,我们有 u k = ∑ i K i t z i k {u}^{k}={\sum }_{i}{K}_{i}^{t}{z}_{i}^{k} uk=∑iKitzik。以 z k z_k zk为条件,并且仅计算关于 i k i_k ik的梯度估计的期望(4.9b),
这与(3.5b)中的精确梯度一致。换句话说,原始更新方程(4.9c)的随机梯度是无偏的:(4.9b)和(4.9c)平均与(3.5b)一致(Lan和Zhou 2018)。在两种特定采样方案,均匀采样和数据自适应采样下,针对I型问题显示了(4.9)的线性收敛。步长参数 σ , τ 和 θ σ,τ和θ σ,τ和θ通常取决于强凸参数μ和采样方案{ p i p_i pi}。(Shalev-Shwartz和Zhang 2013,Shalev-Shwartz 20152016)进一步分析了随机双坐标上升和方差减少随机梯度之间的关系。
21删去与(4.7)中h的定义相对应的因数1/n。
| 算法4.3 (4.8)的随机原始-对偶混合梯度(SPDHG)。 |
|---|
 |
算法4.3中所示的SPDC的一个变体在(Chambolle等人2018年)中提出,并在(Alacaoglu等人2019)中进一步分析,具有额外的收敛性质。与(4.9)相比,主要区别在于原始更新(第6,7行)的梯度估计 K ~ x \tilde K_x K~x结合了(4.9d)的双重更新和双重外推步骤,后者类似于确定性PDHG的双重外推变体(Chambolle等人,2018年)。对于III型问题,当步长参数 τ i , σ i τ_i,σ_i τi,σi对所有i满足 p i − 1 τ i σ i ∥ K i ∥ 2 < 1 {p}_{i}^{-1}{\tau }_{i}{\sigma }_{i}\parallel {K}_{i}{\parallel }^{2}\lt 1 pi−1τiσi∥Ki∥2<1时,算法4.3的收敛速度是O (1/k),关于期望的原始-对偶间隙(Chambolle等人2018年,Alacaoglu等人2019年)。
我们对算法4.3的介绍比(Chambolle等人2018年)要简化得多,以便与SPDC(张和肖2017,兰和周2018)进行比较和得出联系。最初的出版物(Chambolle Et Al 2018)允许完全算子值步长参数,即 σ i , τ i σ_i,τ_i σi,τi可以是对称的正定矩阵 S i , T i S_i,T_i Si,Ti使得 ∥ S i 1 / 2 K i T i 1 / 2 ∥ 2 < p i \parallel {S}_{i}^{1/2}{K}_{i}{T}_{i}^{1/2}{\parallel }^{2}\lt {p}_{i} ∥Si1/2KiTi1/2∥2<pi。此外,随机抽样方案(算法4.3的第3行)可以更灵活,例如,可以一起选择对偶变量组,只要采样在每个对偶变量被选择为正 p i p_i pi的意义上是“适当的”。此外,使用类似于确定性PDHG算法3.4的更复杂的、自适应的步长参数,可以实现I类和II类问题的加速收敛。感兴趣的读者请参阅(Chambolle等人,2018年)以了解完整的概括。
4.4.其他随机算法
我们提出的两个原始-对偶算法,SPDC(4.9)和SPDHG,都执行对偶变量的随机更新。对于以下问题
min x f ( x ) + h ( K x ) , f ( x ) = ∑ i f i ( A i x ) (4.15) \min_xf(x)+h(Kx),f(x)=\sum_if_i(A_ix)\tag{4.15} xminf(x)+h(Kx),f(x)=i∑fi(Aix)(4.15)
其中 f i f_i fi是 L i L_i Li-光滑的,f(x)是μ-强凸的,μ>=0,h是凸的,非光滑的,基于确定的原始对偶不动点算法(Chen Et Al 2013),在(朱和张2020a,2021)中提出了一种随机原始对偶算法,该算法对原始变量(x)进行随机更新。在每次迭代中,x更新使用估计的梯度来 ∇ ~ f ( x ) \tilde ∇f(x) ∇~f(x)近似∇f(x)。在不使用减方差技术的情况下,证明了第I类问题的次线性收敛是递减步长的(朱和张2020)。当结合SVRG中的VR技术来计算 ∇ ~ f \tilde{{\rm{\nabla }}}f ∇~f时,收敛速度被改进为固定步长的线性(朱和张,2021)。同样的算法也适用于具有O(1/k)收敛的III型问题。
问题模型(4.15)也以对偶形式进行了研究,即
min y i , z f 1 ∗ ( y 1 ) + . . . + f n ∗ ( y n ) + h ∗ ( z ) s . t . A 1 t y 1 + . . . + A n t y n + K ∗ z = 0 (4.16) \min_{y_i,z}f_1^*(y_1)+...+f_n^*(y_n)+h^*(z)\\\tag{4.16} s.t. A_1^ty_1+...+A_n^ty_n+K^*z=0 yi,zminf1∗(y1)+...+fn∗(yn)+h∗(z)s.t.A1ty1+...+Antyn+K∗z=0(4.16)
问题(4.16)可以看作是3-块ADMM(3.15a)的多块推广。就像2-块ADMM到3-块ADMM的扩展可能不收敛一样,3-块ADMM能否推广到多块并保持收敛也是未知的。然而,对于第I类问题(Suzuki 2014),可以证明(4.16)的随机化多区块ADMM线性收敛。此外,在(Dang和Lan 2014)中研究了随机化原始-对偶算法和随机化多块ADMM之间的关系,使得一种算法的收敛结果和参数设置可以适用于另一种算法。
4.5.应用程序
在这里,我们应用SPDHG(算法4.3)来解决我们的原型重建问题(3.22)。代替(3.24)中的重新表述,我们可以将目标函数(3.22)按下式分解
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4f00gatM-1658667535661)(https://s2.loli.net/2022/07/23/cbEYTpwDo1AMmas.png)]
其中 A j A_j Aj是第j个(组)投影视图的投影算子, y j 、 w j y_j、w_j yj、wj是相应的测量投影数据和统计权重。应用(4.17b)的有限和部分中的 1 2 ∥ ⋅ ∥ w j 2 \tfrac{1}{2}\parallel \cdot {\parallel }_{{w}_{j}}^{2} 21∥⋅∥wj2和 H ~ i {\tilde{H}}_{i} H~i的共轭关系,我们得到以下对偶表示:
可分离的对偶变量为 z i , ξ j z_i,ξ_j zi,ξj,其中 i = 1 , . . . , I i=1,...,I i=1,...,I, j = 1 , . . . , J j=1,...,J j=1,...,J。由于抽样方案的灵活性,我们可以从两组中的每一组中随机抽样一个对偶变量。也就是说,每次更新涉及投影视图的一个子集和正则化的一个子集。因此,算法4.3实例化为以下步骤:
1.从 1 , … , J {1,…,J} 1,…,J中抽取随机变量 j k j_k jk,从 1 , . . . , I {1,...,I} 1,...,I中抽取随机变量 i k i_k ik,使得。 P r o b ( i k = i ) = p i ( 1 ) \mathrm{Prob}({i}_{k}=i)={p}_{i}^{(1)} Prob(ik=i)=pi(1)和 P r o b ( j k = j ) = p j ( 2 ) \mathrm{Prob}({j}_{k}=j)={p}_{j}^{(2)} Prob(jk=j)=pj(2)执行随机双重更新。
根据我们的假设,这两个更新都可以以封闭的形式执行。特别地,从(4.18a)开始,对于 j = j k j=j_k j=jk,我们有
2.根据(4.12)更新梯度估计
3.原始的更新:
由于假设G(X)是简单的,因此它也可以以闭合形式获得。通过设置θ=1和步长来保证收敛
我们可以利用数据拟合项 F j ( x ) F_j(x) Fj(x)的二次型,获得对投影视图的子集应用梯度下降的算法,而不是经历共轭函数 1 / 2 ∥ ⋅ ∥ w j − 1 2 1/2\parallel \cdot {\parallel }_{{w}_{j}^{-1}}^{2} 1/2∥⋅∥wj−12并使用(4.19)来更新对偶变量 ξ ξ ξ。这就产生了算法4.4,其推导见附录A.4。它是SPDHG的一种应用,它用一种特殊的对角预条件子 S j = w j − 1 σ j − 1 {S}_{j}={{w}_{j}}^{-1}{\sigma }_{j}^{-1} Sj=wj−1σj−1来代替(4.19)中的标量 1 / σ j 1/σ_j 1/σj。由于我们假设统计权重被归一化,使得 w j ≤ 1 w_j ≤ 1 wj≤1,所以(4.22)中的步长选择仍然有效。
| 算法4.4 应用SPDHG方法求解(3.22)。 |
|---|
 |
4.6.讨论
我们提出了Prox-SVRG、Katyushans和SPDHG三种算法,它们分别直接解决类型I、类型II和类型III问题。在机器学习中,为解决一类问题而开发的算法可以通过“还原”技术间接解决另一类问题(Shalev-Shwartz和Zhang 2014, Lin等人2015,Allen-Zhu和Hazan 2016)。 μ 2 ∥ x − x ~ ∥ 2 ; \tfrac{\mu }{2}\parallel x-\tilde{x}{\parallel }^{2}; 2μ∥x−x~∥2;或类型III问题可以通过(1)添加一个小的二次项和(2)对非光滑的Lipschitz组件应用平滑技术来制成类型I。然后将求解第一类问题的算法应用于增广问题。事实上,由于第I类问题在机器学习中普遍存在,许多随机算法,如(Prox-)SVRG、SDCA (Shalev-Shwartz和Zhang 2013)、SPDC (Zhang和Xiao 2017),最初是为了解决第I类问题而开发的,然后使用还原技术扩展到其他问题类型(Shalev-Shwartz和Zhang 2016, Lan和Zhou 2018)。该思想与确定性一阶算法中使用的类似,参见e.g. (Nesterov 2005, Devolder et al 2012)。但是二次项增广会改变目标函数和解,导致解的偏差。为了消除解决偏差,经常需要通过更新 x ~ \tilde{x} x~或根据使用内外部循环算法结构的调度减少二次常数μ。这种间接方法往往不如直接方法实用:为了达到最佳的收敛速度,内环算法的求解精度和参数调度都需要控制,这是通过估计最优函数值和/或估计到解x*的距离来实现的。
我们的讨论集中在确定性、有限和目标函数的随机化算法上,因为它们是图像重建最常见的模型。对于特殊的数据密集型应用,例如单程PET重建(Reader Et Al 2002),我们可能只看到每个数据样本一次。假设确定性有限和目标函数的方差减少技术将不适用,我们不得不求助于经典的随机梯度下降(SGD)算法(4.3)。这类经典的SGD算法也可以受益于Nester ovʼ的动量技术(Devold等人,2014年,Kim等人,2014年)。对于 min x ϕ ( x ) = f ( x ) + g ( x ) {\min }_{x}\phi (x)=f(x)+g(x) minxϕ(x)=f(x)+g(x)的复合非光滑凸问题,其中f是L光滑的,g是MLipschitz的,加速随机逼近(AC-SA)算法(LAN 2012)相当于将算法3.5的第3行替换为
其中$\tilde{{\rm{\nabla }}}\phi 是 f 的一般 ( 次 ) 梯度估计。假设 是f的一般(次)梯度估计。假设 是f的一般(次)梯度估计。假设\tilde{{\rm{\nabla }}}\phi 是无偏的,且具有有限方差 σ 2 ,则在适当的步长参数下,即 是无偏的,且具有有限方差σ2,则在适当的步长参数下,即 是无偏的,且具有有限方差σ2,则在适当的步长参数下,即θ_k,γ_k ,在 ( L a n 2012 ) 中证明了 A C − S A 能够达到 ,在(Lan 2012)中证明了AC-SA能够达到 ,在(Lan2012)中证明了AC−SA能够达到{ \mathcal O }(\tfrac{L}{{k}^{2}}+\tfrac{M+\sigma }{\sqrt{k}}) 的收敛速度,这与复杂性理论 ( N o m e r o v s k i 和 Y u d i n 1983 ) 所规定的下界一致。尽管光滑分量 f 的加速使 的收敛速度,这与复杂性理论(Nomerovski和Yudin 1983)所规定的下界一致。尽管光滑分量f的加速使 的收敛速度,这与复杂性理论(Nomerovski和Yudin1983)所规定的下界一致。尽管光滑分量f的加速使{ \mathcal O }(\tfrac{1}{{k}^{2}})$的速度很快,但梯度估计(σ)的有限方差导致了M-Lipschitz非光滑函数g的 1 / k 1/\sqrt{k} 1/k收敛速度慢于 1 / k 1/\sqrt{k} 1/k的收敛速度。
5.非凸优化中的凸性
非凸优化比凸优化具有更大的挑战性。为了获得高效有效的解,有必要将结构引入到非凸性中。在这种情况下,凸性在非凸优化中也扮演着重要的角色。非凸目标函数通常可以分解为凸的、非凸的、光滑的或非光滑的分量。不同的组合产生了不同的非凸优化模型。
在本文中,我们首先介绍了一些与非凸优化有关的基本定义,其中一些定义是从凸集到非凸集的推广,然后讨论了两类问题的求解算法:带弱凸正则的凸优化和基于模型的非凸优化。弱凸函数是可以被强凸函数‘纠正’的非凸函数。一个突出的例子是使用弱凸正则化的图像去噪,其中整个目标函数可以保持凸,而不考虑非凸正则。对于基于模型的非凸优化,我们讨论了形式为 g ( x ) + h ( K x ) g(x)+h(Kx) g(x)+h(Kx)的复合目标函数,其中g是光滑的,h可以是光滑的、非光滑的、凸的或非凸的。然后,不同的问题模型会导致不同的求解算法。
5.1.基本定义
其中L>0是梯度∇f的李普希兹常数。(Nester ov等人2018年,引理1.2.3),(5.1)等价于![]()
请注意,对于上界上的凸函数,(5.2)与(2.2)重合;对于下界,光滑的凸函数满足比非凸函数( − L ∥ x − y ∥ 2 / 2 −L∥x−y∥^2/2 −L∥x−y∥2/2)更紧的下界(0)。给定(5.2),可以证明 L 2 ∥ x ∥ 2 − f ( x ) \tfrac{L}{2}\parallel x{\parallel }^{2}-f(x) 2L∥x∥2−f(x)是凸 22 ^{22} 22,其梯度简单地为 L x − ∇ f ( x ) Lx−∇f(x) Lx−∇f(x)。这一观察结果得出如下结论:任何具有Lipschitz连续梯度的光滑f都可以写成凸(DC)函数的差,即![]()
其中f1和f2都是凸的。对于满足(5.2)的f,我们总是可以选择 f 1 = L 2 ∥ x ∥ 2 {f}_{1}=\tfrac{L}{2}\parallel x{\parallel }^{2} f1=2L∥x∥2和 f 2 = L 2 ∥ x ∥ 2 − f ( x ) {f}_{2}=\tfrac{L}{2}\parallel x{\parallel }^{2}-f(x) f2=2L∥x∥2−f(x),它们都是凸的。一般而言,给定DC分解(5.3),如果f1是L-光滑的,而f2是L-光滑的,那么我们有![]()
在不失去一般性的情况下,我们总是可以假设 0 < l < = L 0
DC函数包含一大类非凸函数。许多流行的非凸正则化子,如极小极大凹罚(张氏等2010)、光滑截断绝对偏差(Fan和Li 2001)、对数先验 l o g ( 1 + ∣ x ∣ / u ) log(1+|x|/u) log(1+∣x∣/u)、截断 l 1 ( m i n { ∣ x ∣ , L } ) l_1(min\{|x|,L\}) l1(min{∣x∣,L}),对于某些 L > 0 L>0 L>0和 l 1 − l 2 ( ∥ x ∥ 1 − α ∥ x ∥ 2 l_1-l_2(∥x∥_1−α∥x∥_2 l1−l2(∥x∥1−α∥x∥2,对于 x ∈ R n x\in R^n x∈Rn, 0 < α < 1 0<α<1 0<α<1(Lou和Yan2018)都是DC函数。见(Hartman等人1959,Le Thi and Dinh 2018,de Oliveira 2020)。除了光滑函数外,DC函数还包括另一个重要的子类,即弱凸函数,其特征为![]()
22使用凸函数通过其线性逼近是下界的定义。
在我们引用的DC例子中,截断的L1和L1-L2不是弱凸的,而其余的是弱凸的。
近邻映射和莫罗包络在非凸分析中仍然占据着重要的位置。回想一下它们的定义: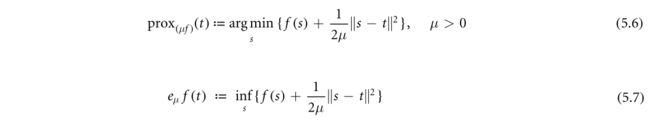
从(Rockafella and Wets2009,定理1.25)出发,设 f : R d → ( − ∞ , ∞ ] f:R^d→(−∞,∞] f:Rd→(−∞,∞]是真闭函数,且 i n f f > − ∞ inf f>−∞ inff>−∞。则对任意μ>0,(5.6)的 P r o x μ f ) ( t ) Prox_{μf)}(t) Proxμf)(t)非空紧, e μ f ( t ) e_{μf}(t) eμf(t)在(x,μ)中有限连续.。
在这里,我们比较和对比三个案例:
- 如果f是凸的,则 P r o x μ f ( t ) Prox_{μf}(t) Proxμf(t)对μ>0的存在唯一性来自于目标函数(5.6)的强凸性,且包络(5.7)是具有1/μ-Lipschitz梯度的光滑包络.。
- 如果f是一般的非凸函数,则近似映射(5.6)可以是多值的,并且Moreau包络是连续的,但不一定是光滑的。
- 如果f是σ-弱凸的,则对 μ < σ − 1 , f ( s ) + 1 / ( 2 μ ) ∥ s − t ∥ 2 μ<σ^{−1},f(s)+1/(2μ)∥s−t∥^2 μ<σ−1,f(s)+1/(2μ)∥s−t∥2是强凸的,最小化问题(5.6)是强凸的且有唯一解;Moreau包络是具有Lipschitz梯度的光滑的.。对于 μ < σ − 1 μ<σ^{−1} μ<σ−1, P r o x μ f ( t ) Prox_{μf}(t) Proxμf(t)和 e μ f ( t ) e_{μf}(t) eμf(t)的性质类似于一般非凸函数的性质。
许多非凸函数都很简单,因为它们的近似映射(5.6)要么以封闭形式存在,要么很容易计算。我们在附录A.5中提供了一个近端映射计算(5.6)的例子,强调了与非凸性相关的一些特性。
对于非凸极小化,由于通常不存在整体解,收敛通常用临界(或稳定)点来刻画:迭代{ x k x_k xk}使得 x k → x ∗ x_k→x^* xk→x∗,其中 x ∗ x_* x∗是由 0 ∈ ∂ ϕ ( x ∗ ) 0 \in ∂\phi(x_*) 0∈∂ϕ(x∗)刻画的目标函数 ϕ \phi ϕ的临界点,而 ϕ ( x ) \phi(x) ϕ(x)是 ϕ \phi ϕ的极限次微分。对于非凸函数,极限次微分是将次微分从凸集扩展到非凸集的少数特征之一(Rockafella and Wets 2009,第8章)。它与凸函数的(正则)次微分相一致。
5.2.具有弱凸正则项的凸优化
Moreau包络(5.7)提供了构造非凸正则的一般方法。设 h ~ ( x ) \tilde h(x) h~(x)是一个Lipschitz连续凸函数,即 ∥ h ~ ( x ) − h ~ ( y ) ∥ ≤ Ω ∥ x − y ∣ ∣ , Ω > 0 ∥\tilde h(x) − \tilde h(y)∥≤Ω∥x−y||,Ω>0 ∥h~(x)−h~(y)∥≤Ω∥x−y∣∣,Ω>0。用 e μ h ~ e_μ\tilde h eμh~表示它的Moreau包络,它是凸光滑的,具有梯度Lipschitz常数1/μ。可以证明(内斯特罗夫2005)![]()
换言之, e μ h ~ e_μ\tilde h eμh~可以看作是(潜在的非光滑的) h ~ \tilde h h~的光滑逼近,并且逼近精度可以由μ控制。规定![]()
然后 0 < = h < = u Ω 2 / 2 0<=h<=uΩ^2/2 0<=h<=uΩ2/2。显然,h有DC分解;而且,h总是弱凸的,因为莫罗包络 e μ h e_μh eμh可以被一个强凸函数‘修正’: − e u h ~ ( x ) + σ 2 ∣ ∣ x ∣ ∣ 2 -e_u\tilde h(x)+\frac{\sigma}{2}||x||^2 −euh~(x)+2σ∣∣x∣∣2可以通过有 σ > u − 1 σ>u^{-1} σ>u−1来凸化。作为这种构造的一个例子,如果 h ~ ( t ) = α ∣ t ∣ \tilde h(t)=\alpha|t| h~(t)=α∣t∣,则h是极小极大凹罚(Mcp)(Ahn等人2017年,Selesnick等人2020年)。
对于图像去噪,复合目标函数的形式为 f ( x ) = g ( x ) + λ h ( K x ) f(x)=g(x)+λh(Kx) f(x)=g(x)+λh(Kx),其中g是ρ-强凸数据拟合项,λ>0是惩罚权重,K是促进变换域稀疏的线性算子。使用(5.9)中所示的h的DC结构,我们有![]() [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lIGKev2d-1658667535672)(https://static.iopscience.com/2.80.0/img/lazy-loading-placeholder.gif)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lIGKev2d-1658667535672)(https://static.iopscience.com/2.80.0/img/lazy-loading-placeholder.gif)]
由于 e u h ~ ( K ) e_u\tilde h(K) euh~(K)是光滑的,且具有梯度Lipschitz常数 ∥ K ∥ 2 / ( 2 μ ) ∥K∥^2/(2μ) ∥K∥2/(2μ),如果选择惩罚权值λ使得 0 < = λ ∥ K ∥ 2 / μ < ρ 0<=λ∥K∥^2/μ<ρ 0<=λ∥K∥2/μ<ρ,则数据拟合项的强凸性可以抵消h(K·)的弱凸性。目标函数仍然是强凸的,这可以通过我们在3.1节中讨论的凸优化算法来处理。例如,通过根据(5.10)分割目标,然后使用近端梯度下降法,如果合成(K·)的近端映射易于计算,如果不容易计算,则使用原始-对偶或ADMM。在这些方法中,由于(5.10)的(带下划线的)第一项是光滑的,它通常被用(2.2)的二次上界代替。由于其特殊的结构,其梯度计算可以方便地得到为 ∇ g ( x ) − λ K t ∇ e μ h ~ ( K x ) ∇g(x)−λK^t∇e_μ\tilde h(Kx) ∇g(x)−λKt∇eμh~(Kx),其中![]()
换句话说,我们不需要Moreau包络的显式表达式来计算它的梯度;知道近邻映射就足够了。当莫罗信封没有闭合形式的表达式时,这个快捷方式变得很方便,例如,参见(Xu And Noo 2020)。
上述方法引入一个弱凸正则并将其合并到一个全局凸优化问题中,严重依赖于目标函数中一个分量的强凸性。因此,这种方法似乎仅限于具有小惩罚权重λ的图像去噪。在图像复原等应用中,数据拟合项g(·)是由一个线性算子A构成的,由于A的非空零空间,该合成g(Ax)可能不是强凸的,这一局限性可以使用(Lanza等人2019,Selesnick等人2020)中提出的广义Moreau包络来部分解决。考虑以下问题模型, 23 ^{23} 23![]()
矩阵B是待定的半正定矩阵。如果 k e r ( K ) ⋂ k e r ( B ) = ϕ ker(K)\bigcap ker(B)=\phi ker(K)⋂ker(B)=ϕ,则得到(5.12)的inf(Lanza等人2019),并且可以用min代替。在此条件下,很容易证明 1 2 ∣ ∣ x ∣ ∣ B 2 − M h B ( x ) \frac{1}{2}||x||^2_B-M_h^B(x) 21∣∣x∣∣B2−MhB(x)是一个凸函数.。这一性质将有助于指定矩阵B,使得整个目标函数 ϕ ( x ) \phi(x) ϕ(x)(5.11)是凸的。首先,将 ϕ ( x ) \phi(x) ϕ(x)重写为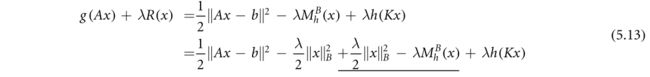
在(Lanza等人,2019)中提出了两种选择B的策略,其中一种需要对 A t A A^{tA} AtA进行特征值分解。一旦保证了凸性,就可以应用一些一阶凸算法来求解极小化问题。(Lanza等人,2019)的数值研究显示了良好的收敛特性,并证明了非凸正则化子在图像去模糊和修复应用中的优越性能。
虽然这种方法在理论上很有吸引力,但对于以A为正投影算子的图像重建而言,仍存在许多问题。首先,用于图像重建的二次数据拟合项通常涉及依赖于数据的统计权重。在这种情况下,条件(5.14)应替换为 A t d i a g ( w ) A > = λ B A^tdiag(w)A>=λB Atdiag(w)A>=λB,其中 0 < = w < R p 0<=w
到目前为止讨论的两种方法,在目标具有或不具有强凸性的情况下,共享它们依赖于弱凸正则的显式DC分解的特征,如果这样的分解不容易获得,这可能是一个限制。在某些情况下,在不知道DC函数的显式分解的情况下使用它会更方便。(Mollenhoff Et Al 2015)中的方法可以被视为朝着这个方向迈出的一步。它考虑了和以前一样的问题模型,
23与(Lanza等人,2019年)相比,这是一个简化的模型。感兴趣的读者可以参考(Lanza等人,2019)了解更多细节。
![]()
其中g是ρ-强凸的,h是ω-弱凸的。Mollenhoff等人(Mollenhoff Et Al 2015)提出的算法直接在强凸g和弱凸h之间分裂,避免了h的显式DC分解和分量重组。
Mollenhoff等人(Mollenhoff Et Al 2015)中的直接分裂依赖于PDHG算法(3.5)的“Primal Only”版本(Strekalovski And Cremers 2014),该算法最初是针对诸如(5.15)这样的问题提出的,其中每个分量g和h都要求是凸的。PDHG算法以交替的方式计算g和h的近邻映射,其中h是h的凸共轭。原始的仅有版本的PDHG使用Moreau恒等式(2.12)用h的近邻映射替换h的近邻映射。当g和h都是凸的时,所得到的算法(5.16)等价于原PDHG,并且它直接适用于非凸问题。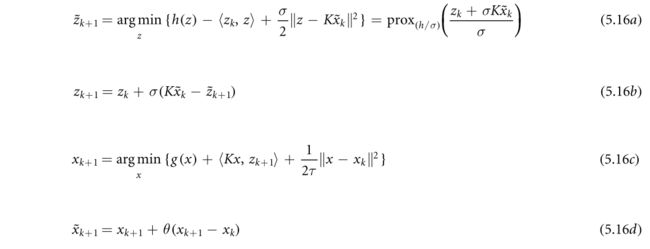
请注意,前两步(5.16a)和(5.16b)相当于PDHG的(3.5a),其余步骤(5.16c)和(5.16d)与PDHG相同。常数σ,τ,θ是要确定以确保收敛的步长参数。
设h是ω-弱凸的,g是ρ-强凸的,使得 ρ < ω ∥ K ∥ 2 ρ<ω∥K∥^2 ρ<ω∥K∥2.这些条件保证(5.15)的 ϕ ( x ) \phi(x) ϕ(x)是强凸的.。用 x ∗ = arg min x ϕ ( x ) {x}_{* }={\arg \,\min }_{x}\phi (x) x∗=argminxϕ(x)表示唯一的极小元。在(Mollenhoff Et Al 2015)中证明了:如果 σ = 2 ω σ=2ω σ=2ω,且 σ τ ∥ K ∥ 2 < = 1 στ∥K∥^2<=1 στ∥K∥2<=1, θ ∈ [ 0 , 1 ] θ\in[0,1] θ∈[0,1](5.16)的 x k x_k xk以1/k的速度以遍历方式收敛到 x ∗ x_* x∗,换句话说,设 x ˉ k = ∑ i k x i / k {\bar{x}}_{k}={\sum }_{i}^{k}{x}_{i}/k xˉk=∑ikxi/k,则 ∥ x ˉ k − x ∗ ∥ 2 ⩽ C / k \parallel {\bar{x}}_{k}-{x}_{* }{\parallel }^{2}\leqslant C/k ∥xˉk−x∗∥2⩽C/k。当g是凸的,但不是强凸的,在h可微、 ∇ h ∇h ∇h一致有界等附加假设下,证明了序列 x k , z k , z ~ k x_k,z_k,\tilde z_k xk,zk,z~k保持有界.
请注意,由于h是ω-弱凸的,则设置σ>ω已经保证了子问题(5.16a)解的唯一性。然而,正如(Mollenhoff等人,2015年)所分析的那样,更大的参数大小要求 ( σ = 2 ω ) (σ=2ω) (σ=2ω)对于确保收敛既是必要的,也是充分的。
我们注意到,就收敛速度而言,(5.16)不是最优的:由于目标是强凸的,所以这类问题的最优收敛速度是 ϕ ( x k ) − ϕ ( x ∗ ) ∼ O ( 1 / k 2 ) \phi ({x}_{k})-\phi ({x}_{* })\sim { \mathcal O }(1/{k}^{2}) ϕ(xk)−ϕ(x∗)∼O(1/k2)。如果存在h的显式DC分解,则可以通过对凸分量进行重组和分裂,并应用最优一阶算法来获得最优码率。然而,(5.16)有趣的是,它直接在凸和非凸分量函数之间拆分,并且可以应用于真正的非凸问题。事实上,正如数值研究(Mollenhoff等人,2015)所证明的那样,(5.16)在非凸问题上的实际收敛超出了理论保证。
5.3.基于模型的非凸优化
其中f(x)是具有Lipschitz连续梯度的非凸光滑的,h是潜在的非光滑的非凸的,但从它的近邻映射(5.6)容易计算的意义上来说是简单的。
我们讨论了两类目标函数(5.17)的求解算法:(1) K = I K=I K=I和(2) K ≠ I K≠I K=I。许多非凸算法已经被用来解决第一类问题:对于h是凸的和f是光滑非凸的特殊情况,近似梯度下降型算法至少可以追溯到(Fukushima和Mine1981)。当线性算子K存在时,即对于类型2问题,如果非凸函数h是光滑的,那么大量的算法是可用的,以梯度下降型和ADMM的形式;如果h是非光滑的,则算法选项变得更加依赖于模型。我们将讨论非光滑h和线性算子K在不同假设下的可用算法选项。
5.3.1.类型1:ϕ=f+h,f非凸光滑的,h简单,K=I
用于非凸优化的经典近似梯度算法(Nester ov 2013,Teboulle 2018)采用以下形式: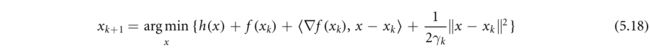
如果不存在h,(5.18)简化为用于平滑非凸最小化的梯度下降算法。如果h是凸的,(5.18)中的目标函数是强凸的,因此序列{ x k x_k xk}是唯一定义的。如果{ x k x_k xk}有界,则可以通过设置步长 γ k γ_k γk来确保收敛到f的临界点,使得 γ k = γ < = 1 / L f γ_k=γ<=1/L_f γk=γ<=1/Lf, L f L_f Lf是f的梯度Lipschitz常数(Attouch和Bolte 2009,Attouch等2013,Bolte等2014)。请注意, x k x_k xk的边界可以通过f的水平集的边界来保证,如果f和h都是矫顽的,或者如果h是矫顽的,则可以确保xk的边界,并且$\inf f\gt -\infty $。
对基本算法(5.18)的推广一直在不同的方向上进行。我们将这些发展归结为两类:(1)h是凸的,(2)h是非凸的。
继续h是凸的情况,非凸优化的惯性近似算法(IPiano)(Ochs等人2014)在(5.18)中加入了惯性项。IPiano的通用版本如下:![]()
与(5.18)相比,在更新方程 x k + 1 x_{k+1} xk+1中加入了一个附加的“惯性项” β k ( x k − x k − 1 ) β_k(x_k−x_{k−1}) βk(xk−xk−1)。如果对所有k都有 β k = 0 β_k=0 βk=0,则(5.19)与(5.18)相同。在(Ochs Et Al 2014)中的数值例子表明,通过设置 β k β_k βk>0,惯性项可以帮助克服虚假驻点并达到较低的目标值。
为了保证(5.19)的收敛,提出了各种步长策略。最简单的情况是恒定步长设置,需要 β k = β ∈ [ 0 , 1 ) β_k=β\in[0,1) βk=β∈[0,1)和 γ k = γ < 2 ( 1 − β ) / L f γ_k=γ<2(1−β)/L_f γk=γ<2(1−β)/Lf。在这样的参数设置下,如果目标 ϕ \phi ϕ是强制的,则目标函数 ϕ ( x k ) \phi(x_k) ϕ(xk)收敛,来自(5.19)的序列{ x k x_k xk}保持有界,并且整个序列{ x k x_k xk}收敛到 ϕ \phi ϕX的临界点。 24 ^{24} 24此外,由 u k = min 0 < + k < + K ∣ ∣ x k − x k − 1 ∣ ∣ 2 u_k=\min_{0<+k<+K}||x_k-x_{k-1}||^2 uk=min0<+k<+K∣∣xk−xk−1∣∣2的收敛速度被证明为 u k O ( 1 / k ) u_k~O(1/k) uk O(1/k)(Ochs等人2014)。
(5.19)的更新方程看起来像Fista(另外还要求f是凸的)。事实上,已经针对与iPiano相同类别的目标函数研究了一种类似Fista的算法,称为近邻梯度外推(PGE)(Wen等人,2017)。(5.20)中给出了PGE的更新方程。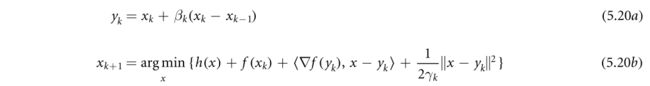
比较(5.20)和(5.19),唯一明显的区别在于(5.20b):f的梯度在外推点 y k y_k yk处求值,而在(5.19b)中,梯度在当前估计的 x k x_k xk处求值。
外推参数 β k β_k βk(5.20a)依赖于(5.4)的精化梯度连续性质。设f对 l f l_f lf和 L f L_f Lf满足(5.4)。(Wen Et Al 2017)证明了:如果 γ k = 1 / L f γ_k=1/L_f γk=1/Lf,且外推参数 β k β_k βk使得 0 < = β k < = β < L f L f + l f 0<=β_k<=β<\sqrt{\frac{L_f}{L_f+l_f}} 0<=βk<=β<Lf+lfLf,则(5.20)的序列 x k x_k xk是有界的,如果目标 ϕ \phi ϕ有有界下水平集;在附加的(局部)误差界假设(Wen Et Al 2017)下,假设3.1, 25 ^{25} 25目标 ϕ ( x k ) \phi(x_k) ϕ(xk)是R-线性收敛的,并且PGE(5.20)的序列 x k x_k xk也是R-线性收敛到 ϕ \phi ϕ的临界点。
当f是凸时,则 l f = 0 l_f=0 lf=0, β k β_k βk的上界为 L f L f + l f = 1 \sqrt{\frac{L_f}{L_f+l_f}}=1 Lf+lfLf=1,这是由FISTA的参数设置所满足的。该文(Win Et Al 2017)随后得出结论:具有固定重启方案(例如,当k=0, β k = k / ( k + 3 ) β_k=k/(k+3) βk=k/(k+3), k = 0 , . . . , K − 1 k=0,...,K−1 k=0,...,K−1,且有固定K,使得 β k < = β < 1 β_k<=β<1 βk<=β<1成立)的FISTA也是R-线性收敛的。请注意,这是一个局部收敛结果;我们前面引用的结果是全局的,例如目标的 O ( 1 / k 2 ) O (1/k^2) O(1/k2)(Beck和Teboulle 2009)或迭代的收敛(Chambolle 2015)。现
在我们考虑将(5.18)推广到h为非凸的情况。首先,我们观察到h的近端映射可能是多值的,这促使对(5.18)进行如下修改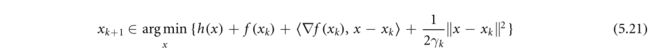
24全序列的收敛要求目标函数满足Kurdyka-Lojasiewicz(KL)性质。请参见第5.4节。
25松散地说,这个假设表明,如果从(5.20b)开始的连续迭代是“接近”的,那么可以保证迭代是“接近”到驻点集的。
其中唯一的变化是允许 x k + 1 x_{k+1} xk+1是 p r o x ( γ k h ) {\mathrm{prox}}_{({\gamma }_{k}h)} prox(γkh)的最小化集合中的任何一个。26另一个区别是为了确保收敛,步长参数需要更小,即 γ k γ_k γk被选择为使得 0 < γ ‾ < γ k < γ ‾ < 1 / L f 0\lt \underline{\gamma }\lt {\gamma }_{k}\lt \overline{\gamma }\lt 1/{L}_{f} 0<γ<γk<γ<1/Lf。另一方面,对于(5.18)中的h凸,步长γ的上界确实是 2 / L f 2/L_f 2/Lf(Bolte等人,2014)。在步长较小的情况下,如果(1)序列{ x k x_k xk}是有界的,并且(2)函数 ϕ \phi ϕ满足Kurdyka-Lojasiewicz(KL)性质,则建立了{ x k x_k xk}到目标f的临界点的全局收敛(Atouch等人2013,Bolte等人2014),这两个性质都可以针对成像问题中的典型目标函数来验证。
正如我们在5.1节中讨论的,许多非凸函数都有DC分解,设 h = h 1 − h 2 h=h_1−h_2 h=h1−h2,其中 h 1 h_1 h1和 h 2 h_2 h2都是凸的。通常情况下, h 1 h_1 h1的近端标测比h的近端标测更容易评估。
这样的例子包括 l 1 − l 2 l1-l2 l1−l2势函数(Lou和Yen 2018)、MCP(Zhang Et Al 2010)、SCAD(Fan和Li 2001)和之前的日志 l o g ( 1 + ∣ x ∣ / e ) log(1+|x|/e) log(1+∣x∣/e)。在除第一个例子之外的所有例子中,分量H2是具有Lipschitz连续梯度的光滑的。对于这样的非光滑非凸h,目标函数可以重写为:![]()
其形式为光滑非凸分量 f ( x ) − h 2 ( x ) f(x)−h_2(x) f(x)−h2(x)加上非光滑凸分量 h 1 h_1 h1。则基本近端梯度算法(5.18)和惯性/动量变量iPiano(5.19)或Pge(5.20)都适用于使用根据(5.22)的ϕ的分裂来求解(5.22),即 f − h 2 f−h_2 f−h2和 h 1 h_1 h1。
我们刚刚概述的这个想法是(Wen Et Al 2018)中所做研究的一个特例,它研究了PGE(5.20)的一个变种,称为带外推的凸算法的近似差分,在f是光滑的CCP的条件下,以及在较少限制的条件下, ∇ h 2 ∇h_2 ∇h2是局部Lipschitz连续的。在ϕ的有界水平集,ϕ是 K L KL KL函数等标准假设下,建立了收敛和收敛速度。
与如(5.21)中那样根据f和h的直接分割相比,(5.22)的基于DC的分割在步长参数方面可能具有一些优势。当 ∇ f ∇f ∇f和 ∇ h 2 ∇h_2 ∇h2都是全局Lipschitz连续时,分裂的步长(5.22)取决于 ∇ f − ∇ h 2 ∇f−∇h_2 ∇f−∇h2的Lipschitz常数,即 m a x { L h 2 , L f } max\{L_{h_2},L_f\} max{Lh2,Lf}。 27 ^{27} 27用(5.18)或其变体实现(5.22)的步长可以逼近 2 / max { L f , L h 2 } 2/\max \{{L}_{f},{L}_{{h}_{2}}\} 2/max{Lf,Lh2},当 L h 2 < 2 L f {L}_{{h}_{2}}\lt 2{L}_{f} Lh2<2Lf时,步长大于使用(5.21) 1 / L f 1/L_f 1/Lf的步长。较大的步长与动量/惯性选项相结合可以改善经验收敛。
5.3.2.类型2:ϕ=fx) +hK ),f非凸光滑的,h简单的
文献对于类型2问题变得更加具体,其中K是非平凡的线性映射,并且当h是非凸和非平滑时更是如此。如果h是光滑的,我们总是可以将其与平滑分量f分组,并应用梯度下降算法(5.18)进行非凸平滑最小化。这种重组可以增加梯度Lipschitz常数,这减小了步长参数。因此,即使简单的梯度下降算法工作,分割目标函数并分别处理每个分量在计算上也是有利的。下面我们讨论类型2问题的算法选项,将h平滑或不平滑的情况分开。
如果h是光滑的,则ADMM的许多非凸变体(Li和Pong 2015,Hong等2016,Guo等2017,Liu等2019,Wang等2019)是潜在适用的。与应用ADMM的典型做法一样,我们首先将优化问题重新表述为以下约束形式![]()
然后,ADMM通过更新关于拉格朗日的x、z和λ继续进行。结果表明,如果惩罚参数ρ足够大,28则迭代收敛到目标函数的一个临界点。不同的论文(Hong et al 2016,Guo et al 2017,Liu et al 2019)考虑了不同的问题模型,都包括(5.23)作为特例,一些工作,例如(Li and Pong 2015,Liu et al 2019),也考虑了线性化和/或近似化简子问题。根据问题模型,提供了合格惩罚ρ的下限。
26在用于凸优化的3-块ADMM中也出现了这种更新方案的低于规格的情况。Cf算法3.3。
27通过假设f和h2都是凸的,cf(5.3),(5.4)。
28对于凸问题,惩罚权重ρ只要求为正;ρ的值可能会影响收敛速度。对于非凸问题,存在一个下界ρ0,使得需要ρ和ρ0来确保收敛。
(Hong et al 2016,Guo et al 2017,Liu et al 2019)中收敛的一个必要条件是线性算子K是满列阶的。当K是2D和3D图像的常规有限差分算子时,K具有由恒定图像组成的零空间,因此不是满列秩(也不是满行秩)。这一条件可以使用略微修改的有限差分算子K的定义来满足,如在(Liu等人2021A)中所讨论的。或者,如果数据拟合项f(x)包含另一个线性算子(例如,正投影算子),如 f ~ ( A x ) + h ( K x ) \tilde{f}({Ax})+h({Kx}) f~(Ax)+h(Kx),则该问题可以被重新表示为![]()
如果层叠矩阵 [ A t ∣ K t ] t {[{A}^{t}| {K}^{t}]}^{t} [At∣Kt]t具有满列秩且等价于 ∅ = K e r ( A ) ∩ K e r ( K ) \varnothing =\mathrm{Ker}(A)\cap \mathrm{Ker}(K) ∅=Ker(A)∩Ker(K),则可将来自Hong等人2016年、郭某等人2017年、Liu等人2019年的ADMM应用于有限差分矩阵的传统定义。
除了非凸ADMM外,块坐标下降算法还可以应用于光滑h(K·)的第二类问题,只要h是另一个非凸非光滑函数的Moreau包络(5.7)。在这种情况下,目标可以重写为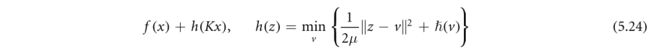
其中 h ~ \tilde h h~是非凸的,可能是非光滑的,而μ>0是表征h和 h ~ \tilde h h~之间的‘接近’的参数(另见(5.8),当?是凸的情况)。这种‘半二次’表达式(Nikolova和Ng 2005,Nikolova和Chan 2007)对于大量的非凸函数是已知的,例如见(Wang等人2008)。此外,如果h是可分的,这是我们在(4.7)中使用随机原始对偶算法时利用的一个性质,则h可以进一步分解为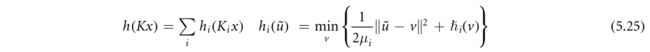
其中未知数是x和来自半二次形式的辅助变量{ v i v_i vi}。目标函数(5.26)由光滑的非凸分量(带下划线的项)和可能的非光滑、非凸的块可分分量组成。这种特殊的结构使得它适用于适用于非凸问题的块坐标下降(BCD)算法,例如Palm(Bolte等人2014)或其惯性版本(Pock和Sabach 2016),以及BCD算法(Xu和Yen 2013,2017)。作为一个简单的2块示例,这些BCD算法使用以下问题模型:![]()
其中 r 1 r_1 r1和 r 2 r_2 r2是真闭的, H ( ⋅ , ⋅ ) H(·,·) H(⋅,⋅)是这样的:对于固定的 x 2 x_2 x2, H ( ⋅ , x 2 ) H(·,x_2) H(⋅,x2)是光滑的,具有Lipschitz梯度常数 L 1 ( x 2 ) L_1(x_2) L1(x2),对于任何固定的 x 1 x_1 x1, H ( x 1 , ⋅ ) H(x_1,·) H(x1,⋅)都有一个梯度Lipschitz常数 L 2 ( x 1 ) L_2(x_1) L2(x1)。Palm通过应用近端梯度下降并以交替的方式更新块变量来进行: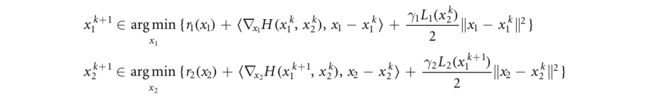
其中 γ 1 , 2 γ_{1,2} γ1,2>1是步长参数。这样的方案也可以扩展到多块设置。如果正则化子 γ 1 , 2 γ_{1,2} γ1,2是凸的,或者如果光滑分量H是多凸的,即,关于每个未知的块 x i x_i xi但不是联合的凸的,则可以使用更大的步长和更大的外推参数(Bolte等人2014,Xu和Yen 2017)。
半二次形式(5.24)也揭示了处理非平滑非凸复合正则化的可能方法。直观地说,常数μ(5.24)越小,越接近 h μ h_μ hμ≡ h近似于 h ~ \tilde h h~。 29 ^{29} 29(Rockafellar和Wets 2009),定理1.25。在固定的μ下,目标 f ( ⋅ ) + h μ ( K ⋅ ) f(·)+h_μ(K·) f(⋅)+hμ(K⋅)可以用Lipschitz连续梯度微分,因此可以应用梯度下降来降低目标;作为μ→ 0,目标接近 f ( ⋅ ) + h ~ ( K ⋅ ) f(·)+\tilde h(K·) f(⋅)+h~(K⋅),它是非凸的和非平滑的。如果与梯度下降相结合,参数μ作为迭代的函数减小,则可以合理地预期解接近非平滑目标 f ( ⋅ ) + h ~ ( K ⋅ ) f(·)+\tilde h(K·) f(⋅)+h~(K⋅)的解。已经针对凸问题研究了应用平滑最小化来解决非平滑问题的这种想法(Nesterov 2005,Tran Dinh 2019,Xu和Noo 2019)。
29这里 h μ ≡ h h_μ≡h hμ≡h,下标μ使对μ的依赖显式。
对于非凸极小化,在(Bohm and Wright,2021)中研究了同样的思想,用于处理非光滑、弱凸、复合正则化 h ~ ( K ⋅ ) \tilde h(K·) h~(K⋅)。所提出的可变平滑算法将梯度下降与依赖迭代的递减的平滑参数序列 μ k μ_k μk相结合如下: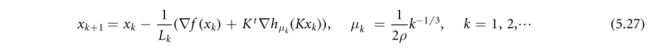
其中 L k L_k Lk是 f ( ⋅ ) + h μ ( K ⋅ ) f(·)+h_μ(K·) f(⋅)+hμ(K⋅)的迭代依赖梯度Lipschitz常数,ρ h ~ ( v ) \tilde h(v) h~(v)的弱凸性参数,即 h ~ ( v ) + ρ ∥ v ∥ 2 / 2 \tilde h(v)+ρ∥v∥^2/2 h~(v)+ρ∥v∥2/2是凸的.。注意,梯度评估hμ可以获得如下所示![]()
由 h ~ ( v ) \tilde h(v) h~(v)是ρ-弱凸的,因此 v ∗ v^* v∗在(5.28)中对 μ < ρ − 1 μ<ρ^{−1} μ<ρ−1唯一定义,这是对所有k(5.27)满足 μ k μ_k μk的一个条件。假设 h ~ ( v ) \tilde h(v) h~(v)是Lipschitz连续的,建立了(5.27)的收敛和收敛速度以及一个改进的时序形式(Bohm and Wright,2021)作为梯度次优性的判据和一个可行条件。
5.4.讨论
正如我们前面提到的,对于非凸、非光滑的复合问题,文献变得更加特定于模型。对于ADMM类型的算法,我们只关注那些使用光滑非凸正则的算法。事实上,有大量的非凸ADMM算法可以处理非光滑、非凸的复合h(K·)。例如,(Bot等人,2019)考虑了以下问题模型![]()
其中关于h和K的假设与前面一样,f是Lipschitz连续梯度可微的,g类似于h,h可以是非凸的,非光滑的,也可以是简单的。这个问题模型可以被视为Palm(Bolte等人2014)的推广,其中一个近似项h现在进一步由线性算子K组成,它还包括我们的第二类问题作为特殊情况,即当未知的y和g不存在时。
在(Bot等人,2019年)中提出了一种完全分裂的admm算法,分别利用g,h和线性算子K的近邻映射,以及梯度 ∇ f ( x , y ) ∇f(x,y) ∇f(x,y)。所提出的算法的收敛要求K是满行(满射),这是处理非光滑复合函数的其他ADMM算法共享的共同假设,例如见(Li和Pong 2015,Sun等人2019)。如果K是一维信号的有限差分运算符,则K是整行秩值(Willms 2008)。对于2-D或3-D问题,K不是完整的行阶;这个问题在2019年通过放松来规避(Sun等人,2019)。还有专门的ADMM算法(You等人2019,Liu等人2021A),它们与特定的非凸非光滑复合正则化和/或数据拟合项一起工作。论文(Liu等人2019)汇编了一个相当全面的不同ADMM算法的列表,以及它们特定的问题模型和收敛要求。
我们遇到了一些具有不同的凸(DC)分解的函数,例如,所有具有Lipschitz连续梯度的可微函数都是DC的(此外,所有多元多项式都是DC函数(BAčák和Borwein 2011),以及许多非光滑函数被不断地发现具有DC分解(Nouiehed Et Al 2019)。DC函数的普适性使得DC规划和凸差算法成为非凸规划的一个重要分支,可以利用凸优化的工具进行算法设计和分析。作为一个最简单的例子,考虑 min x f 1 ( x ) − f 2 ( x ) \mathop{\min }\limits_{x}{f}_{1}(x)-{f}_{2}(x) xminf1(x)−f2(x),其中 f 1 , f 2 f_1,f_2 f1,f2都是凸的。DCA首先使用其共轭函数将 f 2 f_2 f2重写为 f 2 ( x ) = max y ⟨ x , y ⟩ − f 2 ∗ ( y ) {f}_{2}(x)=\mathop{\max }\limits_{y}\langle x,y\rangle -{f}_{2}^{* }(y) f2(x)=ymax⟨x,y⟩−f2∗(y),然后将目标扩充为 min x , y f 1 ( x ) − ⟨ x , y ⟩ + f 2 ∗ ( y ) \mathop{\min }\limits_{x,y}{f}_{1}(x)-\langle x,y\rangle +{f}_{2}^{* }(y) x,yminf1(x)−⟨x,y⟩+f2∗(y)。然后,DCA以交替的方式关于x和y最小化。由于迭代k中关于y在 x k x_k xk处的最小化等价于设置 y ∈ ∂ f 2 ( x k ) y\in∂f_2(x_k) y∈∂f2(xk),DCA与迭代线性化(Candes et al 2008,Ochs et al 2015)、优化-最小化(Hunter and Lange2000,2004)以及凸凹过程(Yuille And Rangarajan 2003)密切相关。传统上,DCA通常依赖于凸规划的迭代子问题求解器,这使得它们不能完全分裂。最近的DCA结合了邻近梯度映射等元素,以致子问题可以具有闭合形式的解(温等人,2018年,Banert和Bot,2019)。DCAS适用于各种非凸问题,包括稀疏优化(Gotoh等人2018)和压缩传感(Zhang和Xin 2018),它们与图像中的反问题重叠。鼓励感兴趣的读者参考这些最先进的发展(Le Thi and Dinh 2018,d e Oliveira 2020)。
对于非凸极小化问题,收敛证明的一般公式可以在(Atouch等人2013,Bolte等人2014,Teboulle 2018)中找到。考虑这样的问题: min F ( x ) \min \ F(x) min F(x),并假设一个算法为k=1,L生成迭代{ x k x_k xk}。为了证明 x k x_k xk收敛到F的一个临界点,公式相当于(1)证明子序列收敛,(2)证明整个序列收敛。第一步取决于特定的算法结构,可以通过序列{xk}上的几个条件(充分下降、次梯度界和极限连续性)来建立(Atouch等人,2013)。第二步,验证整个序列的收敛,需要对目标F附加一个假设,并且独立于具体的算法。另外的假设是F满足(非光滑)Kurdyka-Lojasiewicz(KL)性质,该性质通过再参数函数来刻画F在临界点x*处的‘锐性’,该函数也称为去零化函数。重新参数化函数的指数,即Lojasiewicz指数,导致Xk的收敛速度估计(Atouch和Bolte,2009,Atouch等人2010)。
我们只讨论了非凸非光滑极小化的确定性算法。在深度神经网络应用的推动下,非凸非光滑优化的随机算法正在经历巨大的发展。这些发展中的问题模型主要集中在第5.3节的第I类问题,这些问题潜在地适用于具有简单的非光滑正则化的非凸极小化问题。这些发展本身仍处于早期阶段;它们的实际影响,特别是在成像应用方面,仍有待调查。最近的出版物(Reddi等人2016年、方等人2018年、Lan and Yang 2019年、Pham等人2020年、Tran-Dinh等人2021年)以及其中的参考文献,应该是一个很好的起点,可以更深入地了解最新发展。
6.凸性、图像重建和DL的协同集成
前几节重点介绍了一阶(非)凸优化算法,这些算法是许多基于模型的图像重建(MBIR)方法的基础,用于CT、MRI、PET和SPECT。在过去的几年里,这些MBIR方法中的许多都已经与DL集成,最著名的是变分网络(VN)的框架(Hammernik等人,2018年)。在VN框架中,整个重建流水线具有类似迭代算法的递归形式,不同之处在于可学习的CNN替换MBIR目标函数中的正则化函数。在更广泛的背景下,DL也开始与MBIR的其他部分进行交互,包括数据获取和超参数(用于正则化)。与此同时,机器学习社区在将凸优化层嵌入到DL网络中、用于结构化或可解释预测或提高数据效率方面进行了积极的研究。简而言之,凸优化层封装了一个凸优化问题(AMOS 2019):正向传递解决给定输入数据的凸优化问题;通过凸优化层的端到端学习需要将解 a r g m i n \mathrm{argmin} argmin的梯度信息反向传播到输入数据。接下来,我们讨论这些最新的研究趋势:(1)嵌入CNN模块作为MBIR重建流水线的一部分,(2)嵌入凸优化模块作为DL流水线的一部分,以及相关的成像应用。
6.1.在MBIR管道中嵌入CNN
我们的原型目标函数(3.22)的传统MBIR方法的一个缺点是,在变换域中编码稀疏性的正则化(3.23)可能过于简化,无法捕捉复杂人体解剖的显著特征。这促使了更复杂的正则化设计,更好地适应当地的解剖结构(Bredie等人2010年、Holt 2014年、Rigie&La Rivière 2015年、Xu和Noo 2020年)。尽管这种手工制作的稀疏变换很复杂,但与使用字典(Xu等人,2012)、专家领域模型(Chen等人,2014)或卷积码(Bao等人,2019)学习稀疏变换的数据驱动方法相比,这种方法往往性能更差。这些学习的变换域稀疏性可以被视为CNN参数正则化的前身。
VN的框架借鉴了第二节中基于分裂的一阶算法的思想,使重建流水线类似于一阶算法的递归结构。重建流水线保留了数据一致性模块,以便受益于人类对底层成像物理的知识;另一方面,通过CNN参数正则化克服了手工制作的正则化的弱点。在实现方面(图1),VN方法将迭代算法展开为固定次数的迭代,每次迭代由数据拟合+正则化/去噪的递归模块填充。整个重建流水线可以在深度学习库(DLL)中以端到端的监督方式进行训练。
30在这里,我们重点介绍DL和MBIR的集成。DL还可以与分析重建集成,例如用于正弦图预处理(Gami和Karl,Lee等人,2018)或学习短扫描权重(WüRFL等人,2018)。
我们讨论的许多一阶算法现在由CNN使用展开和轮回到基于学习的方法来增强。例如,Fista-Net(向等人2021),ADMM-Net(Yang等人2016),学习原始-对偶重构(Adler和Öktem 2018),iPiano-Net(Su和Lian 2020),SGD-Net(Liu等人2021b)和许多其他(Gupta等人2018年)是基于同名的一阶算法以这种方式获得的。
图1 (A)数据一致性(DC)项和正则化(REG)项串联连接的迭代算法。循环符号(绿色)表示迭代的循环性质。(B)变分网络(VN)展开迭代算法,并用CNN代替正则化。多个CNN可以共享权重(对于所有 k , θ k = θ k,θ_k=θ k,θk=θ)或具有不同的权重,尽管前者更遵循迭代算法的递归性质。(A)中的串行连接可以模拟最近梯度或交替更新方案等算法(梁等人,2019年)。并行连接也是可能的,例如,在梯度下降中,这导致了不同的VN架构(梁等人,2019年)。
变化网络导致更可解释的网络体系结构,这是对DL解决方案神秘的黑箱性质的欢迎背离(朱等人2018年,Häggström等人2019年)。另一方面,“变化网络”这个名称可能会产生误导。对于迭代依赖的CNN参数(图1(B)),VN和从中得出它的迭代算法之间的联系被打破。目前还不清楚解决方案(在推理时)是否解决了变分问题(Schonlieb 2019)。在解的稳定性方面,VN和其他黑盒DL方法都显示出关于数据的不连续性(Antun等人,2020)。
除了不稳定的问题外,目前这些基于展开的方法由于CNN训练对GPU内存的要求而难以进行3D重建。这里的内存需求指的是CNN参数加上中间特征映射的组合内存;两者都需要驻留在GPU中,以实现高效的梯度反向传播。记忆问题可以通过贪婪(逐次迭代)训练策略(Wu等人2019年、Lim等人2020年、Corda-D‘ncan等人2021年)而不是端到端训练来缓解。在(Kellman等人2020)中提出了从GPU存储器中移除中间特征地图的另一种策略,该策略使用反向重新计算,该反向重新计算以逐层(即,每次迭代)向后的方式重新计算来自层输出的层输入。同一篇论文(Kellman等人,2020)还讨论了梯度反向传播的其他内存节省策略。例如,由于(Kellman等人2020)的反向重新计算是近似的,如果发生累积的数字错误,则应将其与正向检查点相结合。
VN方法用CNN代替MBIR目标函数中的正则化函数。如图2所示,在MBIR管道中嵌入CNN模块的另一种方法是使用CNN作为未知图像x本身的参数化(Gong等人2018a,2018b)。更具体地说,x被约束为cnn的输出, x = C N N θ ( z ) x=CNN_θ(z) x=CNNθ(z)。如果CNN被预先训练为去噪模块,其输出x自然会抑制噪声并鼓励平滑成像,这对于PET重建是合理的(Gong等人2018a)。对于预先训练的CNN,重建问题被表示为: min x , z f ( A x , y ) \min_{x,z}f(Ax,y) minx,zf(Ax,y),其中 x = C N N θ ( z ) x=CNN_θ(z) x=CNNθ(z),A是正投影矩阵,y是投影数据,f建模数据一致性,这是负泊松对数似然。约束最小化问题然后由ADMM解决,交替最小化两个子问题:(A)更新x,这是一个典型的重建问题,(B)借助于动态链接库ʼ的自动区分能力更新到cnn,z的输入。这种方法的一种变体是在保持输入z固定的同时更新CNN参数θ(因此它的输出x),这可以是相同的患者ʼ的MR或CT图像。在这种情况下,美国有线电视新闻网学习以数据一致性项指导的自监督方式将患者ʼ的MR或CT图像转换为正电子发射计算机断层扫描图像(Gong等人2018b)
CNN可能有助于MBIR的第二个领域是超参数优化。在MBIR目标函数中,学习或手工制作的正则化函数通过一些加权系数与数据拟合项相结合,也称为超参数。超参数调整是一个关键且具有挑战性的问题:关键是因为它直接影响到解的质量;具有挑战性是因为图像质量和超参数之间的关系在定性上得到了理解,但在定量上没有得到很好的表征。目前,超参数整定主要依靠试错法或网格搜索法。这些策略效率低下,并将超参数限制在很小的数量(Abdalah等人,2013年)。理想情况下,超参数应该适应本地图像内容。也就是说,超参数在空间上应该是可变的,并且超参数的数量与图像大小的比例相同。由于搜索空间的大小,网格搜索或试错策略是不可行的。
对于一般的超参数调整,提出了一种新的参数调整策略网络(PTPN)(Shenet Al 2018),该网络可以自动调整空间变化的超参数。PTPN试图模仿人类观察者ʼ关于超参数调整的直觉:如果图像太模糊,则尝试通过减少超参数来减少平滑;如果图像太嘈杂,则尝试相反的操作。在PTPN(Shenet Al 2018)中,这种直觉是使用强化学习的形式主义学习的(Sutton和Barto 2018),特别是通过深度Q网络(Mnih等人2015),该网络在给定图像块的情况下生成对当前超参数的离散化增量。在实现方面,PTPN运行在执行图像重建直到与当前超参数收敛的内循环之外,然后向PTPN提供图像补丁以查看是否需要调整,如果需要,则使用新调整的超参数重新运行内循环。这一过程仍在继续。因此,PTPN确实模仿并自动化了人工调整过程。然而,这种模拟在计算上是昂贵的,因为每个新的测试图像可能需要多次PTPN调谐迭代,每一次迭代都涉及运行内环重建直到收敛。
图2.按照Gong等人2018a的建议,使用CNN对未知图像x进行参数化。经过预先训练以进行图像去噪的CNN的输出是重建图像。图像重建的公式是最小化关于z或θ的损失函数。
强化学习在超参数选择中的另一个应用是在(魏等人2020)中提出的,它专门与即插即用(PNP)MBIR和ADMM相结合。学习的参数包括(A)用信号通知迭代终止的概率0-1触发,以及(B)形式为( σ k , μ k σ_k,μ_k σk,μk)的标量集,其中k是迭代次数, σ k σ_k σk和 μ k μ_k μk分别是PnP模块的先验强度和ADMM的增广拉格朗日中的惩罚参数。与PTPN不同的是,PTPN与迭代算法的收敛解一起工作,(魏等人2020)直接与中间结果一起工作;这加上触发终止的机制可能会导致总体上更有效的参数调整策略。
上述两种方法在某种意义上实现了超参数调整策略,这两种方法都涉及在推理时动态地、依赖于迭代地调整超参数。这两种策略都没有学习将患者数据(或初步重建)映射到所需的超参数的直接函数关系。显式的函数关系可能过于复杂,但CNN的能力恰恰是近似复杂的函数映射。(Xu And Noo 2021)的超参数学习概念旨在直接学习输入和所需超参数之间的CNN参数化函数映射(图3)。训练结构由两个模块串联组成:(1)将患者数据映射到超参数的CNN模块;(2)采用超参数生成重建图像的图像重建模块(例如MBIR或正弦图平滑+FBP)。以地面真实图像作为训练标签,以端到端有监督的方式进行训练。在推理时,可以分离CNN模块和MBIR模块:通过CNN以前馈方式运行患者ʼ的数据来生成超参数;实际的重建可以在动态链接库之外单独执行。
除了超参数学习和正则化设计之外,DL进入MBIR管道的第三个领域是数据采集本身,即学习系统矩阵。
大多数关于系统矩阵或采样模式学习的工作起源于磁共振和超声(Milletari等人,2019年),其中数据采集模式具有更大的灵活性。最近,先进的介入C臂CT系统也出现了基于学习的轨迹优化(Zaech等人,2019)。无论形式如何,系统矩阵学习都会面临一些影响学习策略的常见问题。
-
无论是无参数学习还是参数学习。无参数学习(Stayman和Siewerdsen 2013,Gözcüet al 2018)通常指的是这样一种场景,即存在有限的候选采样模式集,任务是以某种最优方式选择子集。由于子集选择问题的组合性质,通常以贪婪、递增的方式获得最优子集,基于当前候选来选择下一个候选,直到达到性能标准或耗尽扫描时间预算。另一方面,有可能对采样模式进行参数化,并根据这些参数进行优化。然后,可以应用连续优化算法,例如梯度下降(Aggarwal和Jacob 2020)。
-
最佳抽样方案的标准是什么?大多数采样模式学习方法在学习流水线中包含一个重建算子,并对已知的地面真实图像执行监督学习。在这种情况下,最优的标准很简单:使用损失函数来衡量基本事实和重建之间的差异。或者,如果由采样模式参数化的替代图像质量度量可用,则可以直接学习使用回归网络来预测替代度量(Thies等2020)。
图3.(Xu And Noo 2021)中提出的超参数学习框架。由θ参数化的细胞神经网络生成基于优化的图像重建所需的特定于患者的和空间上不同的超参数η。端到端学习需要将从损失到cnn参数θ的梯度反向传播。在测试/推理期间,图像重建模块可以在DL库之外运行
-
临床任务需要线上还是线下学习。线上或主动学习(Zaech等人2019、Zhang等人2019)旨在根据过去的抽样历史预测下一个抽样位置;线下学习是在收购开始之前规定整个抽样方案。对于一些实时收购来说,在线学习可能是唯一的选择。然而,如果预览或快速扫描获取侦察视图是可能的,则可以在捕获开始之前使用它们来规划整个轨迹。
-
系统矩阵学习是单独执行还是与重构学习结合执行。学习系统矩阵可用于固定的重建算法,无论是直接求逆、MBIR方法,还是基于CNN的重建模块(Gözcüet al 2018)。或者,有理由期望联合优化采样模式和重建算子可以利用两者之间的相互依赖并最大化性能(Aggarwal和Jacob 2020,Bahadir等2020)。
总体而言,抽样模式或系统矩阵学习仍然是一个未被探索的研究领域。我们提出了一些常见的设计问题,这些问题可能超越了不同成像模式的界限。系统矩阵学习有可能在其他模式中找到应用,例如用于动态领结设计的CT(Hsieh和Pelc 2013,Huck等人2019),或用于多针孔图案优化的SPECT(Lee等人2014),或基于视图的获取时间优化(Ghaly等人2012,郑Metzler 2012,van der Velden等人2019)。
6.2.在DL流水线中嵌入凸优化层
优化是机器学习和深度学习的基础。在顶层,几乎所有的动态学习训练都是基于最小化一个目标函数,并应用随机梯度下降来获得网络参数。优化也出现在较低的水平上。常见的DL模块,如RELU、Softmax和Sigmoid,可以解释为非线性映射,其中输出是凸优化问题的解(AMOS 2019,第2章)。例如,RELU仅仅是非负性约束的近端映射。Softmax和Sigmoid是使用Bregman距离而不是二次距离的广义近端映射(Nester Ov 2005)。ML社区正在进行积极的研究,将更通用的凸优化层(COL)作为DL的标准模块来注入领域知识,并增加DL网络的建模能力和可解释性。
图4说明了如何将COL用作DL网络中的模块。COL的输入是上一层的输出加上附加的干扰参数;COL层的输出是凸优化问题的解,并用作下一层的输入。
图4.凸优化层(COL)输出凸优化问题 f ( x ; θ ) f(x;θ) f(x;θ)的解,其中θ集输入y和干扰参数η。COL可以作为组件嵌入到更大的网络中。这种网络的端到端培训需要通过argmin实现差异化。
COL的应用可以在强化学习(Amos等人2018)、对抗性攻击规划(Biggio和Roli 2018,Agrawal等人2019a)、元学习(Lee等人2019)以及凸规划的超参数学习(Amos和Kolter 2017,Bertrand等2020,McCann和Ravishankar 2020)中找到。这种深度网络的端到端训练产生的一个基本问题是如何反向传播COL的梯度。更具体地说,COL的前向传递解决了这个问题![]()
其中f是x的一般凸函数,θ将前一层的输入和讨厌的参数进行集中。给定用于训练的损耗函数l(图4中未示出),端到端学习需要将网络 ∇ x ∗ l ∇_{x_*}l ∇x∗l的输出处的梯度反向传播到网络输入 ∇ θ l ∇_θl ∇θl原则上,这种反向传播可以通过应用基本微积分的链规则来获得: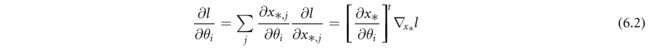
式中, ∇ θ l = [ … ∂ l / ∂ θ i … ] ∇_θl=[…∂l/∂\theta_i…] ∇θl=[…∂l/∂θi…],和 [ ∂ ∗ , j / ∂ θ i … ] j i = ∂ x ∗ / ∂ θ [∂_{*,j}/∂\theta_i…]_{ji}=∂x_*/∂\theta [∂∗,j/∂θi…]ji=∂x∗/∂θ是雅可比矩阵。在实践中,除非问题规模很小,否则更可取的是直接获得 ∇ θ l ∇_θl ∇θl,而不是使用通常不可行的雅可比矩阵来显式地求出矩阵-向量积。
根据凸程序的类型,梯度计算的方法可以大致分为四类:(I)解析微分法,(Ii)展开微分法,(Iii)使用隐函数定理的argmin微分法(Amos和Kolter 2017),以及(Iv)使用不动点迭代的微分法(Griewank和Walther 2008,Jeon等人2021)。我们使用简单(无约束)问题(6.1)来说明这些方法中的关键概念。通常情况下,专门针对一个具体的例子会提供更多信息。在这种情况下,我们考虑以下二次规划问题:
其中θ={q,b},且Q>0,即Q是对称正定矩阵。
-
显然,(6.3)有一个封闭形式的解,即 x ∗ = Q − 1 b x_*=Q_{−1}b x∗=Q−1b。应用于(6.2):
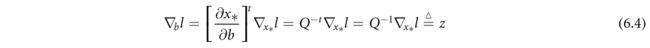
此外,应用矩阵微积分规则: ∂ Y − 1 ∂ t = − Y − 1 ∂ Y ∂ t Y − 1 \frac{∂Y^{-1}}{∂t}=-Y^{-1}\frac{∂Y}{∂t}Y^{-1} ∂t∂Y−1=−Y−1∂t∂YY−1, t ∈ R t\in R t∈R,并将其特化为对称矩阵,
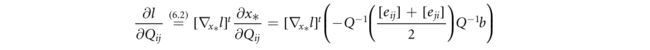
式中 [ e i j ] [eij] [eij]是一个矩阵,除(i, j)以外的所有0的兼容维数为1。将所有元素 ∂ l / ∂ Q i j ∂l/∂Q{ij} ∂l/∂Qij安排成矩阵形式,回顾(6.4)中z的定义,可以验证
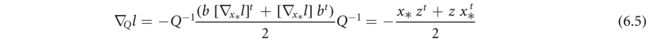
对于反向传递, ∇ b l ∇_bl ∇bl和 ∇ q l ∇_ql ∇ql的额外计算相当于再一次求解(6.3b),其中b被替 ∇ x ∗ l ∇_{x_*}l ∇x∗l换。实际上,不计算矩阵逆 Q − 1 Q^{−1} Q−1;而是通过将共轭梯度算法应用于(6.3)来计算矩阵向量乘积 Q − 1 b Q^{−1}b Q−1b或 Q − 1 ∇ x ∗ l Q^{−1}∇_{x_*}l Q−1∇x∗l。如果解有封闭形式的表达式,则解析微分是可能的,而这对于大多数凸优化问题是不可用的。这一相当严格的要求限制了这种方法在简单问题上的适用性。
-
对于一般设置(6.1),COL的前向传递通常依赖于迭代算法,例如,梯度下降算法。对于具体问题(6.3),梯度下降算法得到以下更新方程:
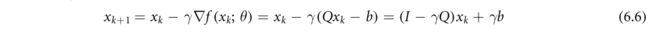
其中, x k x_k xk是第k次迭代时 x ∗ x_* x∗的估计, γ > 0 γ>0 γ>0是步长参数。对于k=0,L,K−1,且设 x ∗ = x k x_*=x_k x∗=xk,展开数量为(6.6)步的递归展开量。由于递归的每一步只包括基本操作(类似于完全连通的层),因此可以从递归的最后一步到第一步来计算反向传递。
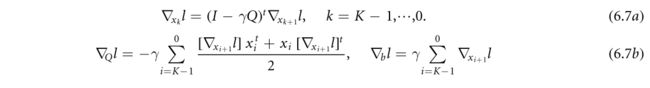
显然,通过展开进行区分需要将所有中间解Xk存储在存储器中,这可能限制展开阶段的数量,并因此限制向前和向后计算的质量
-
一般设置中的Argmin微分从一阶最优性条件开始。也就是说,假设f是可微的,那么我们有 0 = ∇ x f ( x ; θ ) ∣ x ∗ 0=∇_{x}f(x;\theta)|_{x_*} 0=∇xf(x;θ)∣x∗。对于特定问题(6.3),这将导致
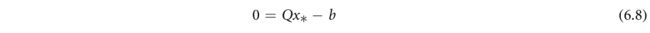
其中,在(6.9)的(A)中,我们设置dQ=0和db=0,以分别导出下两个关系。应用雅可比关系(6.2),基本操作将导致与(6.4)和(6.5)中相同的结果。通过对KKT条件求矩阵微分(Amos和Kolter 2017),Argmin微分已被应用于一般二次规划问题(具有目标函数(6.3)以及线性等式和不等约束)。它还被应用于有纪律的凸规划(Agrawal等人2019a)、锥规划(Agrawal等人2019b)、半定规划(Wang等人2019年)以及其他问题实例,以及在超参数优化和稀疏变换学习中的应用(Bertrand等人2020,McCann和Ravishankar 2020)。Argmin微分法的一个缺点是它是特定于问题的:需要为每类问题推导出梯度反向传播公式。
-
已经在自动微分(或算法微分)的背景下研究了通过迭代算法的固定点的微分,例如见(Christian anson 1994,Griewank and Walther 2008)。最近的一个应用是所谓的定点迭代(FPI)层(Jeon等人2021),用于为DL应用程序建模复杂行为。与前三类不同,通过不动点微分可以应用于更广泛的一类凸问题; 31 ^{31} 31它的实现也很简单,可以通过简单的正演计算来获得。为了说明这一概念,我们应用梯度下降算法作为不动点算法的一个例子来估计(6.3)的解x*。具体地说,对于k=0,…,
-
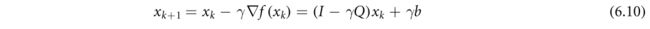
(6.10)的不动点方程满足:
现在区分(6.11)关于b:
请注意,带下划线的术语直接计算为 ( γ Q ) − 1 (\gamma Q)^{-1} (γQ)−1。但这只是因为我们正在处理一个二次问题;采用这条路线将无助于推导出 ∇ b l ∇_bl ∇bl的数值算法,而这正是我们想要做的。因此,我们继续下去,而不是这样的简化。将(6.12)与链规则(6.2)相结合:
将(6.13)中带下划线的项表示为 x ˉ \bar x xˉ,它满足类似于(6.11)的不动点方程,即,
![]()
不动点 x ˉ \bar x xˉ可通过以下方法获得
![]()
这与(6.10)中具有相同步长γ的梯度下降算法相同,但应用于 ∇ x ∗ l ∇_{x_*}l