深度学习笔记1:RNN神经网络及实现
首先贴出一张一般的神经网络应该有的结构图:
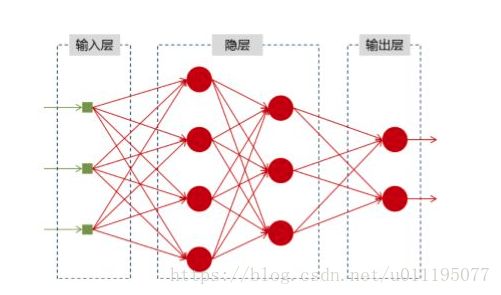
输入层是数据输入层,隐层是模型训练的权重,输出层是经过激活函数后得出的特征。
在深度学习这个领域之中,既然我们已经有了比较完善的人工神经网络和卷积神经网络,那为什么还要用循环神经网络呢?我们知道,一张图片中,各个像素点之间是没有逻辑关系的,我们输入一张图片,无论是在左上角开始输入还是在右下角输入,最终得到的结果分类都是一样的,这也就说明图像之间没有存在必然的逻辑关系。
而且输入输出也是独立的,比如输入两张图片,一张是猫,一张是狗。
但是在我们的现实世界中,有些方面各个元素之间还是有练习的,比如股票的变化,是随着时间的变化而变化的;再比如说自然语言处理当中:“我爱自然语言处理,所以我要学习 ______”;这里填空,我们自然而言的是填写“自然语言处理”了;
这是我们人根据上下文的内容推测出来的;但是这个对于机器而言,要做到这点还是有相当难度的;所以这就要求我们人设计一个网络,使得机器也想人一样能够根据上下文的内容推测下一个输出内容,所以循环神经网络(Recurrent Neural Network,简称RNN)就这样被设计出来,他的本质上就是:像人一样拥有记忆的能力。因此,他的输出依赖当时的输入和记忆。
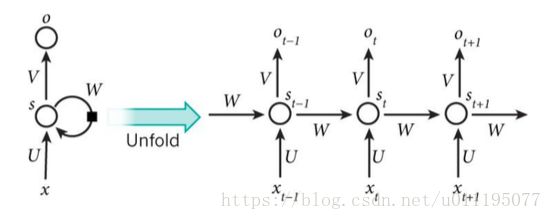
下图是循环神经网络的经典结构图
原则上,我们看左边这个结构就可以了,它也非常形象的说明了循环的含义,右边是展开形式,帮我们理解各个时间点输入时候,该网络是如何工作的。例如这句话“我爱自然语言处理”分为四段‘我’、‘爱’、‘自然语言’、‘处理’, x t − 1 x_{t-1} xt−1=‘我’、 x t x_{t} xt=‘爱’、 x t + 1 x_{t+1} xt+1=‘自然语言’;那么 o t − 1 o_{t-1} ot−1=‘爱’、 o t o_{t} ot=‘自然语言’,那么如果要预测下一个输出 o t + 1 o_{t+1} ot+1是多次呢?通过我们的RNN模型,最大的可能是 o t + 1 o_{t+1} ot+1=‘处理’。当然,具体训练的时候,最终会将文本转换为词向量的。那么根据上述的的映射关系 o = f ( x ) o=f(x) o=f(x)就是根据上图所示。
根据上图: o t = g ( V s t ) o_{t}=g(\mathbf{V}s_{t}) ot=g(Vst)
s t = f ( U x t + W s t − 1 ) s_{t}=f(\mathbf{U}x_{t}+\mathbf{W}s_{t-1}) st=f(Uxt+Wst−1)
所以: o t = g ( V f ( U x t + W s t − 1 ) ) o_{t}=g(\mathbf{V}f(\mathbf{U}x_{t}+\mathbf{W}s_{t-1})) ot=g(Vf(Uxt+Wst−1))
将s的状态不断迭代就可以得到最终的o和x的映射函数
当加上偏置时,一样的,将带入其中:
o t = g ( V s t + b o ) o_{t}=g(\mathbf{V}s_{t}+b_{o}) ot=g(Vst+bo)
s t = f ( U x t + W s t − 1 + b s ) s_{t}=f(\mathbf{U}x_{t}+\mathbf{W}s_{t-1}+b_{s}) st=f(Uxt+Wst−1+bs)
一般我们将f函数记为 f ( z ) = t a n h ( z ) f(z)=tanh(z) f(z)=tanh(z),g函数记为 g ( z ) = s o f t m a x ( z ) g(z)=softmax(z) g(z)=softmax(z) 整个循环神经网络的过程就是在不同时刻输入
图中,U、W、V 都可以看作是权重矩阵,而且在整个到RNN训练过程中都是共享的,也就是说,我们的RNN就是训练这三个权重矩阵而已,相对CNN而言,其训练参数少了非常多了。输入值 x t x_{t} xt在乘于U之后得到 U x t Ux_{t} Uxt,在加上上一时刻的W得到我们的状态 S t S_{t} St,而 V S t VS_{t} VSt在经过激活函数之后得到我们在t时刻的输出 O t O_{t} Ot,下面展示了一个循环神经网络前向传播的过程。

在上图中,假设状态的维度为2,输入、输出的维度都为1,而且全连接层中的权重为:
W r n n = [ 0.1 0.2 0.3 0.4 0.5 0.6 ] W_{rnn}=\begin{bmatrix}0.1 & 0.2\\ 0.3& 0.4\\ 0.5&0.6\end{bmatrix} Wrnn=⎣⎡0.10.30.50.20.40.6⎦⎤
其偏置量的大小为 b r n n = [ 0.1 , − 0.1 ] b_{rnn}=[0.1,-0.1] brnn=[0.1,−0.1]
用于输出的全连接层的权重:
W o u t p u t = [ 1.0 2.0 ] W_{output}=\begin{bmatrix} 1.0 \\ 2.0 \end{bmatrix} Woutput=[1.02.0]
其偏置量的大小为 b o u t p u t = 0.1 b_{output}=0.1 boutput=0.1
那么当在时刻 t 0 t_{0} t0时,作为第一次输入,所以状态state的初始化为 h i n i t = [ 0 , 0 ] h_{init}=[0,0] hinit=[0,0],且当前的输入为1,所以通过拼接向量为 [ 0 , 0 , 1 ] [0,0,1] [0,0,1],通过循环体中全连接的神经网络得到:
t a n h ( [ 0 , 0 , 1 ] ∗ [ 0.1 0.2 0.3 0.4 0.5 0.6 ] + [ 0.1 , − 0.1 ] ) = t a n h ( [ 0.6 , 0.5 ] ) = [ 0.537 , 0.462 ] tanh([0,0,1]*\begin{bmatrix} 0.1 & 0.2\\ 0.3 & 0.4\\ 0.5& 0.6 \end{bmatrix}+[0.1,-0.1])=tanh([0.6,0.5])=[0.537,0.462] tanh([0,0,1]∗⎣⎡0.10.30.50.20.40.6⎦⎤+[0.1,−0.1])=tanh([0.6,0.5])=[0.537,0.462]
这个结果将作为下一刻的输入状态,同时循环神经网络也会使用该状态生成输出:
[ 0.537 , 0.462 ] ∗ [ 1.0 2.0 ] + 0.1 = 1.56 [0.537,0.462]*\begin{bmatrix} 1.0\\ 2.0 \end{bmatrix}+0.1=1.56 [0.537,0.462]∗[1.02.0]+0.1=1.56
依次,可以在下一刻根据上一刻得到的状态继续计算。以下代码为实现过程
#encoding:utf-8
import numpy as np
X=[1,2]
state=[0,0]
#分开定义不同输入部分的权重以方便操作
w_cell_state=np.asarray([[0.1,0.2],[0.3,0.4]])
w_cell_input=np.asarray([0.5,0.6])
b_well=np.asarray([0.1,-0.1])
#定义用于输出的全连接层参数
w_output=np.asarray([[1.0],[2.0]])
b_output=0.1
for i in range(len(X)):
before_activation=np.dot(state,w_cell_state)+X[i]*w_cell_input+b_well
state=np.tanh(before_activation)
final_output=np.dot(state,w_output)+b_output
print "before_activation=",before_activation
print "state=",state
print "final_output=",final_output