曲线的平滑和随机生成

        曲线生成是随机生成算法中不可或缺的基础，
比如之前介绍过的随机生成赛道，第一步就是生成一个好看的平滑曲线。
比如随机生成树木，每一根树枝都可以使用一段横截面曲线沿着另一段路径曲线放样得到。
比如随机生成森林中的藤蔓，可以沿着一些悬链线曲线来使用路径变形动画。 

曲线的差值：
        合理选择差值方式可以生成不同类型的平滑曲线。

//线性插值
vec3 Linear_Interpolate(const vec3& a, const vec3& b, float t)
{
    return a*(1-t) + b*t;
}

//余弦插值，平滑的曲线， x匀速增加 y cos速增加
vec3 Cosine_Interpolate(const vec3& a, const vec3& b, float t)
{
    float t2 = (1 - cos(t * _PI)) * 0.5f;
    return a*(1-t2) + b*t2;
}

//立方插值，非常平滑的结果，不确定能比余弦插值好很多
vec3 Cubic_Interpolate(const vec3& prea, const vec3& a, const vec3& b, const vec3& aftb,float t)
{
    vec3 P = (aftb - b) - (prea - a);
    vec3 Q = (prea - a) - P;
    vec3 R = b - prea;
    vec3 S = a;
    float t2 = t*t;
    float t3 = t*t2;
    return P*t3 + Q*t2 + R*t + S;
}

平滑曲线类型：
        Curve是曲线基类，参见附录源码
        BSpline（B曲线）是控制点平滑曲线，曲线穿过控制点
        HSpline（H曲线）是控制点平滑曲线，每个控制点有两个独立的切线控制手柄，曲线穿过控制点
        贝塞尔曲线，不穿过控制点，（未实现）
        还有很多其它类型的曲线，这里不一一列举了。

随机曲线的生成：暂时总结几种，应该还有很多没发现的其它方法。
    第一种方法，之前在赛道的生成算法中介绍过一种，通过旋转欧拉角逐段向前铺路产生路径曲线。
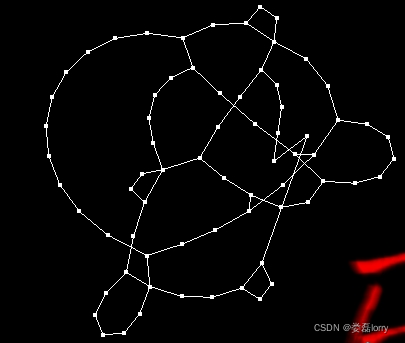
    第二种方法，使用力导图（force-directed-graph）算法，在库伦斥力和弹簧引力共同作用下，布局路点产生网状曲线。有时局部会陷入不太好的平衡状态，需要配合手动辅助布局。    

//力导引算法应用： 1生成随机树 2生成随机赛道
class DiPoint 
{
public:
	DiPoint();
	void SetMass(int mass);

public:
	vec3 pos;
	vec3 normal;		

	float mass;
	float massDev;
	vec3  speed;		
	vec3  force;	
};


class DiSpring
{
public:
	DiSpring();
	bool CalculateForce();

public:
	DiPoint* pointStart;				
	DiPoint* pointEnd;								
	float    originLength;					
};

//
class DiGraph 
{
public:
	DiGraph();
	~DiGraph();
	void Free();
	void LoadFromFile(const char* fileName);
	void Rand();
	void Render();
	void CalculateForce();
	void Solve();
	bool AddSpring(const DiSpring& spring);
	void SetFixedPoint(int index);

public:
	//限制二维
	bool m_bPlane;
	int  m_pointNum;
	int  m_springNum;
	float Ku;
	DiPoint*	m_points;
	DiSpring*	m_springs;	
};


DiPoint::DiPoint()
    : mass(1)
    , pos(0, 0, 0)
    , speed(0, 0, 0)
    , force(0, 0, 0)
{
}

void DiPoint::SetMass(int mass_)
{
    mass = mass_;
    if(mass)
        massDev = 1.0f / mass;
    else
        massDev = 0;	// 没有质量的固定点
}


//==================^_^==================^_^==================^_^==================^_^
DiSpring::DiSpring()
    : originLength(0)
{
}

bool DiSpring::CalculateForce()
{
    //!弹性系数
    float KSpring = 18;//0.8f;
    vec3  difVec = pointStart->pos - pointEnd->pos;
    float difLen = difVec.Length();
    float forceLen;
    vec3  finalforce;
    if(difLen != 0)
    {
        //互斥力 拉力与距离有关
        forceLen = (difLen -  originLength) * 0.5f;
        if(abs(difLen) < 0.00001f)
        {
            difLen = 0.00001f;
        }
        finalforce = difVec * ((forceLen / difLen) * KSpring);
        pointStart->force -= finalforce;
        pointEnd->force += finalforce;
    }
    return 0;
}


//==================^_^==================^_^==================^_^==================^_^
DiGraph::DiGraph()
    : m_points(NULL)
    , m_springs(NULL)
{
}

DiGraph::~DiGraph()
{
    Free();
}

void DiGraph::Free()
{
    SafeDeleteArray(m_springs);
    SafeDeleteArray(m_points);
}

bool DiGraph::AddSpring(const DiSpring& spring)
{
    DiSpring* it = m_springs;
    for(int i = 0; i < m_springNum; i++, it++)
    {
        //if(spring->pointStart->pos == it->pointStart->pos)
        //	if(spring->pointEnd->pos == it->pointEnd->pos)
        //		return true;
        //if(spring->pointStart->pos == it->pointEnd->pos)
        //	if(spring->pointEnd->pos == it->pointStart->pos)
        //		return true;
        if(spring.pointStart == it->pointStart && spring.pointEnd == it->pointEnd)
            return false;
        if(spring.pointStart == it->pointEnd && spring.pointEnd == it->pointStart)
            return false;
    }
    //it->pointStart = spring->pointStart;
    *it = spring;
    m_springNum++;
    return true;
}

void DiGraph::SetFixedPoint(int index)
{
    m_points[index].SetMass(0);
}

void DiGraph::LoadFromFile(const char* fileName)
{
}

void DiGraph::Rand()
{
    Ku = 0;
    m_bPlane = true;
    m_bPlane = false;
    //tree 结构 各层节点数 1 2 4 8 16 32 64
#define  layerNum 7
    int layerNodeNum[7] = {1, 2, 4, 8, 16, 32, 64 };
    int layerBegin[7] = {0, 1, 3, 7, 15, 31, 63 };
    int layerEnd[7]   = {0, 2, 6, 14, 30, 62, 126 };
    m_pointNum = 127;
    m_points = new DiPoint[m_pointNum];
    for(int i = 0; i < m_pointNum; i++)
    {
        m_points[i].mass = 1;
        m_points[i].massDev = 1.0f;
        m_points[i].pos = vec3(RandRange(-10.0f, 10.0f), RandRange(-10.0f, 10.0f), RandRange(-10.0f, 10.0f));
        m_points[i].speed = vec3(0, 0, 0);
    }
    SetFixedPoint(0);
    DiPoint *p1, *p2;
    DiSpring spring;
    m_springNum = 0;
    m_springs = new DiSpring[m_pointNum * 2];
    for(int i = 0; i < layerNum - 1; i++)
    {
        for(int j = 0; j < layerNodeNum[i]; j++)
        {
            p1 = &m_points[layerBegin[i] + j];
            for(int m = 0; m < 4; m++)
            {
                p2 = &m_points[layerBegin[i + 1] + rand() % layerNodeNum[i + 1] ];
                spring.pointStart = p1;
                spring.pointEnd   = p2;
                spring.originLength = 1.0f;
                AddSpring(spring);
            }
        }
    }
}


#define StepTime 0.005f
void DiGraph::CalculateForce()
{
    vec3 zero(0, 0, 0);
    DiPoint* point = m_points;
    for(int i = 0; i < m_pointNum; i++, point++)
    {
        point->force = vec3();
        point->force = (point->mass * vec3(0, -1.1f, 0));
        //特殊力 比如：原点向外的发散力； x轴向两边的发散力
        //限制二维
        if(m_bPlane)
            point->pos.z = 0;
    }
    //计算库仑力，距离平方成反比
    vec3  difVec;
    float difLenSq;
    float difLen;
    DiPoint* point1 = m_points;
    DiPoint* point2 = m_points;
    DiPoint* end1 = m_points + m_pointNum - 1;
    DiPoint* end2 = m_points + m_pointNum;
    float forceKu;
    for(; point1 < end1; point1++)
    {
        point2 = point1 + 1;
        for(; point2 < end2; point2++)
        {
            MinusVec3(difVec, point1->pos, point2->pos);
            difLenSq = difVec.LengthSq();
            difLen = sqrt(difLenSq);
            if(difLen)
            {
                //todo 先适用重力把所有的点悬起来 再慢慢增大库仑力
                forceKu = Ku / difLenSq;
                forceKu = min(3.5f, forceKu);
                difVec *= (forceKu / difLen);
                AddEqualVec3(point1->force, difVec);
                MinusEqualVec3(point2->force, difVec);
            }
        }
    }
    DiSpring* spring = m_springs;
    for(int i = 0; i < m_springNum; i++, spring++)
    {
        spring->CalculateForce();
    }
}

void DiGraph::Solve()
{
    PROFILEFUN("DiGraphObject::Update;", 0.001f, ALWAYSHIDE);
    float stepTime = 0.05f;
    Ku += stepTime;
    if(Ku > 23)
    {
        Ku = 23;
    }
    while(stepTime > _EPSILON)
    {
        float time = Min(stepTime, StepTime);
        CalculateForce();
        vec3 normal(0, 1, 0);
        //float d = 0;
        vec3 addSpeed;
        DiPoint* it = m_points;
        for(int i = 0; i < m_pointNum; i++, it++)
        {
            if(it->mass)
            {
                addSpeed = it->force * it->massDev;
                //StepTime太大不收敛
                it->speed += addSpeed * time;
                it->speed *= 0.998f;
                it->pos += it->speed * time;
            }
        }
        stepTime -= StepTime;
    }
}

void DiGraph::Render()
{
#ifdef CLIENT_APP
    G_RendDriver->SetRenderStateEnable(RS_CULL_FACE, false);
    G_RendDriver->SetRenderStateEnable(RS_TEXTURE_2D, false);
    G_RendDriver->Color3f(0.0f, 1.0f, 0.0f);
    G_RendDriver->RendBegin(RS_LINES);
    for(int i = 0; i < m_springNum; i++)
    {
        G_RendDriver->Vertex3f(m_springs[i].pointStart->pos.x, m_springs[i].pointStart->pos.y, m_springs[i].pointStart->pos.z);
        G_RendDriver->Vertex3f(m_springs[i].pointEnd->pos.x, m_springs[i].pointEnd->pos.y, m_springs[i].pointEnd->pos.z);
    }
    G_RendDriver->RendEnd();
    //
    G_RendDriver->SetPointSize(4.0f);
    G_RendDriver->Color3f(1.0f, 0.0f, 0.0f);
    G_RendDriver->RendBegin(RS_POINTS);
    for(int i = 0; i < m_pointNum; i++)
    {
        G_RendDriver->Vertex3f(m_points[i].pos.x, m_points[i].pos.y, m_points[i].pos.z);
    }
    G_RendDriver->RendEnd();
    G_RendDriver->SetPointSize(1.0f);
 #endif
}

    第三种方法，使用类似布料模拟的弹簧质点模型，固定曲线两端，曲线每个分段处添加质点，给质点添加好重力和弹簧连接。模拟收敛后，曲线呈网形悬链线状，可以模拟森林藤蔓、浮岛吊桥等。
    第四种方法，求解曲线方程。比如根据悬链线两端坐标及悬链线长度求解悬链线方程，再根据方程构筑曲线。解方程的方法有时很难从数学上推导出相应的公式，可以试试通用的迭代法。    

//求过两点p1[x1,y1],p2[x2,y2],长度为len的悬链线方程
bool GetCatenary(const vec2& p1_,const vec2& p2_,double len_, double& A,double& B,double& C)
{
	vec2 p1 = p1_;
	vec2 p2 = p2_;
	double len = len_;

	if (p1.x > p2.x)
	{
		Swap(p1,p2);
	}

	double x1 = p1.x;
	double y1 = p1.y;
	double x2 = p2.x;
	double y2 = p2.y;

	//求曲线弧长的方法   integration{sqrt(dx^+dy^)} =  integration{sqrt(1+(f'(x))^)*dx}

	//悬链线方程：         y = A*cosh(x/A)          准线为x轴，对称轴为y轴
	//过原点的悬链线方程： y = A*(cosh(x/A)-1)
	//悬链线弧长：         len[x1,x2] = A*(-sinh(x1/A)+sinh(x2/A))
	//不定悬链线方程：     y = A*cosh((x-B)/A) + C  准线为y=C轴，对称轴为x=B轴
	//不定悬链线弧长：     len[x1,x2] = A*{-sinh((x1-B)/A)+sinh((x2-B)/A)}    x1EP)
	{
		if (sign <= 0)
		{
			//异号
			if(midVal*leftVal>0)
			{
				left=mid;
				leftVal = Fun(left,userdata);
			}
			else
			{
				right=mid;
				//rightVal = Fun(right,userdata);
			}
		}
		else
		{
			//切于原点？同号 借助导数
			//leftDy = Fun(left+0.0001,userdata) - leftVal;
			midDy  = Fun(mid+0.0001,userdata) - midVal;

			if (leftVal * midDy>0)			//leftVal leftDy必须>0   midDy<则过了过了拐点了
			{
				right=mid;
				rightVal = Fun(right,userdata);
			}
			else
			{
				left=mid;
				leftVal = Fun(left,userdata);
			}
			

			sign = leftVal*rightVal;
		}

		mid=(left+right)/2;
		midVal = Fun(mid,userdata);

		//
		iterNum++;
		if (iterNum==20)
		{
			//尽量更精确
			EP = percise*0.1;
		}
		if (iterNum==30 || iterNum==maxIter)
		{
			//尽量有解
			EP = percise;
		}
		if (iterNum>maxIter)
		{
			return false;
		}
	}

	out_ = mid;
	return true;
}

static double SolveA(double x,double*arr)
{
	//((y1-y2)^-len^)/A^ - {2 - 2*{cosh((x1-x2)/A)}} = 0
	double res = arr[0]/x/x - 2 + 2*cosh(arr[1]/x);
	if (IsInvalidNum(res))
	{
		int a = 0;
	}
	return res;
}
static double SolveB(double B,double*arr)
{
	double len = arr[0];
	double A  = arr[1] ;
	double x1 = arr[2];
	double x2 = arr[3];
	//len + A*(sinh((x1-B)/A) - sinh((x2-B)/A)) = 0
	double res = len + A*(sinh((x1-B)/A) - sinh((x2-B)/A));
	if (IsInvalidNum(res))
	{
		int a = 0;
	}
	return res;
}

有趣的曲线方程：

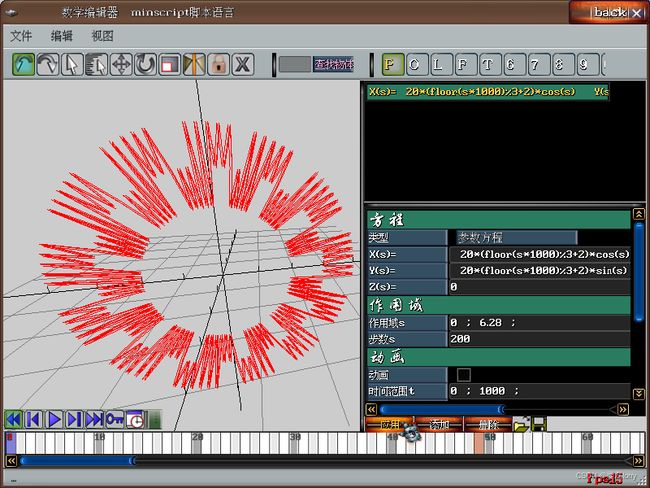
有许多有趣的数学函数对于随机生成曲线也很有帮助。以下截图使用自己编写的“数学函数曲线编辑器”生成，编辑器已上传到资源。

向日葵曲线

    BSpline bspline；int s=0; 
    for (float i=0;i<3.14f*2;i+=0.13f, s++)
    {
        float x = (s%3+2)*cos(i);     
        float y = (s%3+2)*sin(i);     
        bspline.AddKnot(vec3(x,y,0));
    }
    bspline.GenSmoothPoints(10);

//衰减波
    for (float i=0; i<10.0f; i+=1.0f, s++)
    {
        float x = i;
        float y = (s%2)?-i/2.0:i/2.0;
    }

 // 花型线
    x = 20*sin(3.2*s)*cos(s)
    y = 20*sin(3.3*s)*sin(s) 

 

//WANDER曲线
    float s = ang*0.2;// + z; 
    x += 5 * sin(3.12 * s) * cos(1.24 * s);
    y += 5 * sin(2.97 * s) * cos(0.81 * s);
    z += 5 * sin(1.23 * s) * cos(s);

    //周期回归的WANDER曲线
    float s = ang*0.2;// + z; 
    x += 5 * sin(1.23 * s) * cos(1.24 * s);
    y += 5 * sin(1.23 * s) * cos(0.81 * s);
    z += 5 * sin(1.23 * s) * cos(s);

    //内旋轮线(hypotrochoid) ，小圆r绕着大圆R内侧滚动，小圆r内一个点d的运动轨迹线。（点d到小圆r的圆心的距离是d）
     x=(R-r)*cos(ang) + d*cos((R-r)/r*ang);
     y=(R-r)*sin(ang) - d*sin((R-r)/r*ang);

//超圆就是方程式x^a+y^b= c所生成的图形.当a==b==2时,为一个圆
    //超椭圆是m*x^a+n*y^b= c所生成的图形.当a==b==2时,为一个椭圆
    //超圆可能是有倒角的正方形（可能是负倒角）
    //a = rand2(0.1, 10)
    //b = rand2(0.1, 10)
    //x = r*pow_sign(sin(s), a)
    //y = r*pow_sign(cos(s), b)//pow_sign是一个保留正负号的pow
    //static float     pow_sign(float a, float b)
    //{
    //    float s = sign(a);
    //    a = ::fabsf(a);
    //    if (a < FLT_EPSILON)
    //    {
    //        return 0.0f;
    //    }
    //    return ::powf(a, b)*s;
    //}

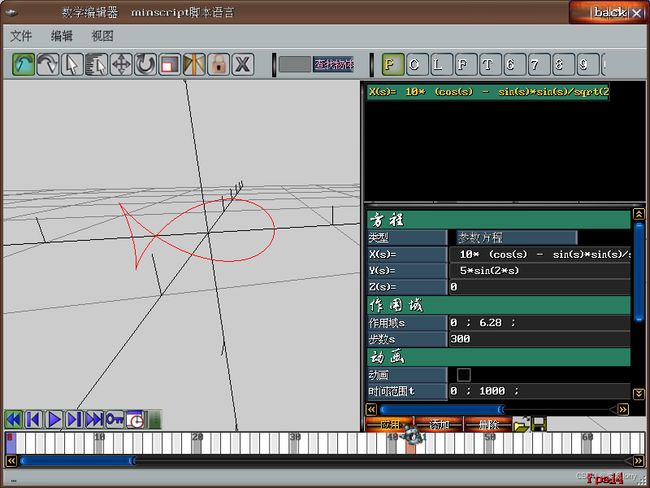
 //    鱼形曲线
         // s = from 0 to (2*PI)
        x = 10* (cos(s) - sin(s)*sin(s)/sqrt(2));
        y = 5*sin(2*s);

//花瓣曲线， 极坐标系
//参数4表现为瓣数， 2.5表现为花瓣内陷度
    r=3*sin(2.5*sin(theta*4.0))   
    

复合随机曲线， 连杆式机械臂末端曲线方程推导:

    可以借助矩阵公式推导器推导出最终表达式，使用随机加速度控制几个角度变量平滑变化产生更复杂的末端运动轨迹。比如平面三连杆，设连杆长度L1、L2、L3，相位T1、T2、T3，则末端位置为：

        x = (((cos(T1)*cos(T2)-sin(T1)*sin(T2))*cos(T3)-(cos(T1)*sin(T2)+sin(T1)*cos(T2))*sin(T3))*L3+((cos(T1)*cos(T2)-sin(T1)*sin(T2))*L2+cos(T1)*L1)); 
        y = (((sin(T1)*cos(T2)+cos(T1)*sin(T2))*cos(T3)+(cos(T1)*cos(T2)-sin(T1)*sin(T2))*sin(T3))*L3+((sin(T1)*cos(T2)+cos(T1)*sin(T2))*L2+sin(T1)*L1)); 

附录 曲线代码

//========================================================
//  @Date:     2016.05
//  @File:     Include/Render/Curve.h
//  @Brief:     Curve
//  @Author:     LouLei
//  @Email:  [email protected]
//  @Copyright (Crapell) - All Rights Reserved
//========================================================

#pragma once

#ifndef  __Curve__H__
#define  __Curve__H__
#include "Math/Mathlib.h"

class File;
class CurvePointArr;
class Curve
{
public:
	Curve();
	Curve(const vec3* knots,int size);
	Curve(const Curve& curve);
	~Curve();

	class Point
	{
	public:
		vec3  pos;
		vec3  tangent; //!front  pre_cur_next三点成角的平分面法线,即切线
		vec3  normal;  //!left   临边所在面的法线，不是角分线取反
		//vec3 up;     //!角分线取反
		vec3  scale;
		float len;     //!距离起点路径欧式长度
	};
	void  Clear();
	void  operator = (const Curve& curve);
	virtual void Render(int opt=0);

	int         GetPointNum() const;
	void        AddPoint(const vec3&  v,int index=-1,bool update=false);
	void        AddPoint(const Point& v,int index=-1,bool update=false);
	void        DelPoint(int index);
	Point*      GetPoint(int index);
	void        SetPoint(int index,vec3& pos,bool update=false);

	bool        GetClosed();
	void        SetClosed(bool closed);

	const vec3	GetGravCenter() const;

	//0~pointnum 根据控制点索引获得位置，可能长度非匀速增长
	vec3        GetPosf       (float pointtime) const;
	const vec3	GetNormalf    (float pointtime) const;
	const vec3	GetTangentf   (float pointtime) const;
	void    	GetPointf     (float pointtime,Point& mixPoint) const;

	vec3        GetPos        (int index)   const;
	const vec3	GetNormal     (int index)   const;
	const vec3	GetTangent    (int index)   const;

	vec3        GetDirToNextPoint(int index)  const ;
	vec3        GetDirToPrevPoint(int index)  const ;


	//获得曲线长度
	float GetCurveLength();
	//path转长度 需要长度均分？
	float Path2Length(float path);
	float Length2Path(float length);

	//获得曲线上最近的点
	float ClosestPath(const vec3& pos);

	//pathInterp  [  ] 
	//lengthInterp  [  ]  [ steps: ]

	Curve&  Transform( const mat4& mat);
	void    Update(int index = -1);

	bool    LoadFromFile(const char* fileName_);
	bool    SaveToFile(File& fileout,const char* space);

protected:	
	CurvePointArr*	m_pPoints;
	vec3		    m_gravCenter;		//重心
	bool		    m_isClosed;		
	float           m_length;
};


class BSplineImp;
class BSpline : public Curve
{
public:
	BSpline();
	BSpline(const vec3* pnts,int size,int divNum);
	~BSpline();
	class Knot
	{
	public:
		vec3  pos;
		vec3  Ax; //m_knotsDirs
		vec3  Bx;
		vec3  Cx;
		vec3  Work;
		vec3  WorkB;

		float  lenRat;
		float  matA;
		float  matB;
		float  matC;
	};
	void  Clear();
	void  operator = (const BSpline& curve);
	virtual void Render(int opt=0);

	int         GetKnotNum() const;
	//!knot操作中没有隐式调用Update函数，因为Update函数代价比较大
	void        AddKnot(const vec3& v);
	void        AddKnot(const Knot& v);
	void        DelKnot(int index);
	Knot*       GetKnot(int index);

	bool GenSmoothPoints(int divNum);

protected:
	BSplineImp*       m_splineImp;
};


class HSplineImp;
class HSpline : public Curve
{
public:
	HSpline();
	HSpline(const vec3* pnts,int size,int divNum);
	~HSpline();
	class Knot
	{
	public:
		int   type;    //0 corner 1单边切线 2双边切线
		vec3  pos;     //控制点
		vec3  tanPos1; //切线控制点
		vec3  tanVec1;       
		vec3  tanPos2; //切线控制点
		vec3  tanVec2; 

		float weight; // artificial weight applied to tangent direction - weights curve more in direction of tangent
	};
	void  Clear();
	void  operator = (const HSpline& curve);
	virtual void Render(int opt=0);

	int         GetKnotNum() const;
	//自动计算切线
	void        AddKnot(const vec3& v);
	//不自动计算切线
	void        AddKnot(const Knot& v);
	void        DelKnot(int index);
	Knot*       GetKnot(int index);

	bool GenSmoothPoints(int divNum);

protected:
	HSplineImp*       m_splineImp;
}; 

#endif

//========================================================
//  @Date:     2016.05
//  @File:     SourceLib/Render/Curve.cpp
//  @Brief:     Curve
//  @Author:     LouLei
//  @Email:  [email protected]
//  @Copyright (Crapell) - All Rights Reserved
//========================================================


#include "General/Pch.h"
#include "Render/Curve.h"
#include "Render/RendDriver.h"
#include 
#include "General/Pce.h"

#pragma warning(disable:4267)
#pragma warning(disable:4018)
class CurvePointArr:public std::vector{};

//#define m_pPoints
Curve::Curve()
:m_isClosed(false)
,m_length(0)
,m_pPoints(NULL)
{
    m_pPoints = new CurvePointArr;
}

Curve::Curve(const vec3* points, int size)
:m_isClosed(false)
,m_length(0)
,m_pPoints(NULL)
{
    m_pPoints = new CurvePointArr;
    if(size >= 0)
    {
        m_pPoints->resize(size);
    }
    if(points)
    {
        for(int i = 0; i < size; i++)
        {
            (*m_pPoints)[i].pos = points[i];
        }
    }
    Update();
}

Curve::Curve(const Curve& curve)
:m_isClosed(false)
,m_length(0)
,m_pPoints(NULL)
{
    this->operator =(curve);
}

Curve::~Curve()
{
    m_pPoints->clear();
    if(m_pPoints)
    {
        delete m_pPoints;
        m_pPoints = NULL;
    }
}

void Curve::operator=(const Curve& curve)
{
    (*m_pPoints) = (*curve.m_pPoints);
    m_gravCenter = curve.m_gravCenter;
}



//bool Curve::LoadFromFile(const char* fileName)
//{
//	Free();
//	File filein;
//	if (filein.Fopen( fileName,"rt"))
//	{ 
//		m_pointsNum = filein.ReadInt();
//		m_points = new CtrlPoint[m_pointsNum];
//
//		for (int loop = 0; loop < m_pointsNum; loop++)
//		{
//			CtrlPoint& frame = m_points[loop];
//			frame.m_time = filein.ReadInt();
//
//			frame.m_rot.x = filein.ReadFloat();
//			frame.m_rot.y = filein.ReadFloat();
//			frame.m_rot.z = filein.ReadFloat();
//
//			frame.m_color.a = filein.ReadFloat();
//		}
//	}
//	return true;
//}
//
//bool Curve::SaveToFile(File& fileout,const char* space)
//{
//	//fileout.Fprintf("\n");
//	fileout.WriteInt(m_pointsNum);
//	fileout.Fprintf("\n");
//	fileout.Fprintf(space);fileout.Fprintf("{");
//	fileout.Fprintf("\n");
//	for (int loop = 0; loop < m_pointsNum; loop++)
//	{
//		CtrlPoint& frame = m_points[loop];
//		fileout.Fprintf(" |  ");fileout.Fprintf(space);
//		fileout.WriteInt(frame.m_time);
//		fileout.Fprintf("[");
//		fileout.WriteFloat(frame.m_rot.x);
//		fileout.WriteFloat(frame.m_rot.y);
//		fileout.WriteFloat(frame.m_rot.z);
//		fileout.Fprintf("]");
//		fileout.WriteFloat(frame.m_color.a);
//		fileout.Fprintf("\n");
//
//	}
//	fileout.Fprintf(space);fileout.Fprintf("}");
//	return true;
//}

void Curve::Clear()
{
    m_pPoints->clear();
}

void Curve::Render(int opt)
{
    G_RendDriver->SetRenderStateEnable(RS_LIGHTING, false);
    G_RendDriver->SetRenderStateEnable(RS_TEXTURE_2D, false);
    G_RendDriver->SetRenderStateEnable(RS_ALPHA_TEST, false);
    G_RendDriver->SetRenderStateEnable(RS_BLEND, false);
    G_RendDriver->SetLineWidth(1.0f);
    G_RendDriver->Color3f(1.0f, 0.0f, 0.0f);
    G_RendDriver->Normal3f(0.0f, 0.0f, 1.0f);
    int pointNum = m_pPoints->size();
    Curve::Point* point1 = GetPoint(0);
	Curve::Point* point2 = GetPoint(1);
    //绘制点 （点选编辑）
    //以线形式绘制
    G_RendDriver->RendBegin(RS_LINES);
    for(int i = 0; i < pointNum-1; i++)
    {
        G_RendDriver->Vertex3fv(&point1->pos.x);
        G_RendDriver->Vertex3fv(&point2->pos.x);
		point1++;
		point2++;
    }
	if (m_isClosed)
	{
		point1 = GetPoint(pointNum-1);
		point2 = GetPoint(0);
		G_RendDriver->Vertex3fv(&point1->pos.x);
		G_RendDriver->Vertex3fv(&point2->pos.x);
	}
    G_RendDriver->RendEnd();
    //G_RendDriver->Color3f(0.0f, 0.0f, 1.0f);
    以面形式绘制
    //G_RendDriver->RendBegin(RS_TRIANGLE_FAN);
    //G_RendDriver->Vertex3f( gravCenter.x,gravCenter.y,gravCenter.z);
    //for (size_t i=0; i<=knotNum; i++)
    //	G_RendDriver->Vertex3f( points[ i%knotNum ].x,
    //	            points[ i%knotNum ].y,
    //				points[ i%knotNum ].z);
    //G_RendDriver->RendEnd();

	//绘制法线
    if(opt&1 && pointNum>0)
    {
        G_RendDriver->Color3f(0.0f, 0.0f, 1.0f);
        G_RendDriver->RendBegin(RS_LINES);
		point1 = GetPoint(0);
        vec3 normal;
        for(int i = 0; i < pointNum; i++)
        {
            normal = point1->pos + point1->normal * 10;
            G_RendDriver->Vertex3fv(&point1->pos.x);
            G_RendDriver->Vertex3f(normal.x, normal.y, normal.z);
			point1++;
        }
        G_RendDriver->RendEnd();
    }
	//绘制切线
    if(opt&2 && pointNum>0)
    {
        G_RendDriver->Color3f(0.0f, 1.0f, 0.0f);
        G_RendDriver->RendBegin(RS_LINES);
		point1 = GetPoint(0);
        vec3 tangent;
        for(int i = 0; i < pointNum; i++)
        {
            tangent = point1->pos + point1->tangent * 10;
            G_RendDriver->Vertex3fv(&point1->pos.x);
            G_RendDriver->Vertex3fv(&tangent.x);
			point1++;
        }
        G_RendDriver->RendEnd();
    }
    //G_RendDriver->SetRenderStateEnable(RS_LIGHTING,true);
    G_RendDriver->SetRenderStateEnable(RS_TEXTURE_2D, true);
    G_RendDriver->Color3f(1.0f, 1.0f, 1.0f);
    //G_RendDriver->PopAttrib();
}


int  Curve::GetPointNum() const
{
    return m_pPoints->size();
}
void Curve::AddPoint(const vec3& v, int index/*=-1*/, bool update/*=false*/)
{
    Point p;
    p.pos = v;
    AddPoint(p, index, update);
}

void Curve::AddPoint(const Point& p, int index/*=-1*/, bool update/*=false*/)
{
    int cur = 0;
    int pointNum = m_pPoints->size();
    if(index < 0 || index >= m_pPoints->size())
    {
        m_pPoints->push_back(p);
        cur = pointNum;
    }
    else
    {
        m_pPoints->insert(m_pPoints->begin() + index, 1, p);
        cur = index;
    }
    if(update)
    {
        Update(cur);
        m_gravCenter = m_gravCenter * pointNum + p.pos;
        m_gravCenter /= (pointNum + 1);
    }
}

Curve::Point* Curve::GetPoint(int index)
{
	//if(index < 0 || index >= m_pPoints->size())
	//	return NULL;

	if(m_pPoints->empty())
		return NULL;

	index %= m_pPoints->size();

    if(index < 0)
        index += m_pPoints->size();

    return &(*m_pPoints)[index];
}
void Curve::SetPoint(int index, vec3& pos, bool update)
{
    if(index < 0 || index >= m_pPoints->size())
        return;
    int pointNum = m_pPoints->size();
    m_gravCenter += (pos - (*m_pPoints)[index].pos) / pointNum;
    (*m_pPoints)[index].pos = pos;
    if(update)
    {
        Update(index);
    }
}

bool Curve::GetClosed()
{
    return m_isClosed;
}
void Curve::SetClosed(bool closed)
{
	m_isClosed = closed;
}
const vec3	Curve::GetGravCenter() const
{
    return m_gravCenter;
}
vec3 Curve::GetDirToNextPoint(int index)  const
{
    int size = m_pPoints->size();
    if(size < 2)
    {
        return vec3();
    }

    if(index < 0 || index + 1 > m_pPoints->size()/*-1*/)
	{
		//index无效
        return vec3();
	}

    int next = index + 1;
    if(next == size)
    {
        if(m_isClosed)
        {
            next = 0;
        }
        else
        {
            index = size - 2;
            next  = size - 1;
        }
    }
    vec3 dir = (*m_pPoints)[next].pos - (*m_pPoints)[index].pos;
    dir.Normalize();
    return dir;
}

vec3 Curve::GetDirToPrevPoint(int index)  const
{
    int size = m_pPoints->size();
    if(size < 2)
    {
        return vec3();
    }
    if(index < 0 || index + 1 > m_pPoints->size()/*-1*/)
        return vec3(0);
    int prev = index - 1;
    if(prev == -1)
    {
        if(m_isClosed)
        {
            prev = size - 1;
        }
        else
        {
            index = 1;
            prev  = 0;
        }
    }
    vec3 dir = (*m_pPoints)[prev].pos - (*m_pPoints)[index].pos;
    dir.Normalize();
    return dir;
}


//0~pointnum 根据控制点索引获得位置，可能长度非匀速增长
vec3 Curve::GetPosf(float pointtime) const
{
	int size = m_pPoints->size();
	if (size<=0)
	{
		return vec3();
	}
	//clamp
	if(pointtime <= 0 )
		return (*m_pPoints)[0].pos;
	if(pointtime > size-1)
		return (*m_pPoints)[size-1].pos;

	int before = pointtime;
	int after  = before + 1;
	if(after >= size)
		return (*m_pPoints)[before].pos;
	return (*m_pPoints)[before].pos * (after - pointtime) 
		+ (*m_pPoints)[after].pos * (pointtime - before);
}

const vec3 Curve::GetTangentf(float pointtime) const
{
	int size = m_pPoints->size();
	if (size<=0)
	{
		return vec3();
	}
	//clamp
	if(pointtime <= 0)
		return (*m_pPoints)[0].tangent;
	if(pointtime > size-1)
		return (*m_pPoints)[size-1].tangent;

	int before = pointtime;
	int after = before + 1;
	if(after >= size)
		return (*m_pPoints)[before].tangent;
	return (*m_pPoints)[before].tangent * (after - pointtime) + (*m_pPoints)[after].tangent * (pointtime - before);
}

void Curve::GetPointf(float pointtime,Curve::Point& mixPoint) const
{
	const int size = m_pPoints->size();
	if (size<=0)
	{
		return;
	}
	//clamp
	if(pointtime <= 0)
	{
		mixPoint = (*m_pPoints)[0];
		return;
	}
	if(pointtime > size-1)
	{
		mixPoint = (*m_pPoints)[size-1];
		return;
	}

	const int before = pointtime;
	const int after = before + 1;
	if(after >= size)
	{
		mixPoint = (*m_pPoints)[before];
		return;
	}
	const float ratBefore = after - pointtime;
	const float ratAfter  = pointtime - before;
	const Point& pointBefore = (*m_pPoints)[before];
	const Point& pointAfter  = (*m_pPoints)[after];
	
    mixPoint.pos     = pointBefore.pos    * ratBefore + pointAfter.pos    * ratAfter;
	mixPoint.tangent = pointBefore.tangent* ratBefore + pointAfter.tangent* ratAfter;
	mixPoint.normal  = pointBefore.normal * ratBefore + pointAfter.normal * ratAfter;
	mixPoint.scale   = pointBefore.scale  * ratBefore + pointAfter.scale  * ratAfter;
}

//0~pointnum 根据控制点索引获得位置，可能长度非匀速增长
vec3 Curve::GetPos(int index) const
{
	const int size = m_pPoints->size();
	if (size<=0)
	{
		return vec3();
	}
	//clamp
	if(index <= 0)
		return (*m_pPoints)[0].pos;
	if(index >= size)
		return (*m_pPoints)[size-1].pos;

	return (*m_pPoints)[index].pos;
}
const vec3	Curve::GetNormal(int index) const
{
	const int size = m_pPoints->size();
	if (size<=0)
	{
		return vec3();
	}
	//clamp
	if(index <= 0)
		return (*m_pPoints)[0].normal;
	if(index >= size)
		return (*m_pPoints)[size-1].normal;

    return (*m_pPoints)[index].normal;
}

const vec3	Curve::GetTangent(int index) const
{
	const int size = m_pPoints->size();
	if (size<=0)
	{
		return vec3();
	}
	//clamp
	if(index <= 0)
		return (*m_pPoints)[0].tangent;
	if(index >= size)
		return (*m_pPoints)[size-1].tangent;

    return (*m_pPoints)[index].tangent;
}

Curve&   Curve::Transform(const mat4& mat)
{
    const int ptNum = m_pPoints->size();
	Point* point = NULL;
	if(ptNum>0)
		point = &(*m_pPoints)[0];
    for(int i = 0; i < ptNum; i++)
    {
        point->pos = mat * point->pos;
		point++;
    }
    Update();
    //m_gravCenter = mat*m_gravCenter;
    return *this;
}

void Curve::Update(int index)
{
    {
        const int ptNum = m_pPoints->size();
		//重心
		m_gravCenter = vec3();
        Point* point = NULL;
		if(ptNum>0)
			point = &(*m_pPoints)[0];
        for(int i = 0; i < ptNum; i++)
        {
            m_gravCenter += point[i].pos;
        }
        if(ptNum>0)
			m_gravCenter /= (float)ptNum;

		//长度
		m_length = 0;
		if(ptNum>0)
			point[0].len = 0;
		for(int index = 1; index < ptNum; index++)
		{
			point[index].len = point[index-1].len + (point[index].pos-point[index-1].pos).Length();
			m_length = point[index].len;
		}

		if(m_isClosed && ptNum>1)
			m_length += (point[ptNum-1].pos-point[0].pos).Length();;

#define _EPSILON 0.0001
        //法线
        vec3 prev;
        vec3 next;
        for(int index = 0; index < ptNum; index++)
        {
            prev = GetDirToPrevPoint(index);
            next = GetDirToNextPoint(index);
            //一部分是直线的情况?
            vec3 midAng = prev + next;
            int tempP = index;
            int tempN = index;
            int PN = 0;
            while(midAng.LengthSq() < _EPSILON)
            {
                if(tempN >= ptNum - 1 && tempP <= 0)
                {
                    break;
                }
                if(tempN < ptNum - 1
                   && (PN == 0 || tempP <= 0)
                  )
                {
                    tempN++;
                    next = GetDirToNextPoint(tempN);
                    PN = 1;
                }
                else if(tempP > 0)
                {
                    tempP--;
                    prev = GetDirToPrevPoint(tempP);
                    PN = 0;
                }
                midAng = prev + next;
            }
            vec3 normal = next.Cross(prev);
            normal.Normalize();
            point[index].normal = normal;
        }

        //切线：角分面法线
        for(int index = 0; index < ptNum; index++)
        {
            //path的法线和角分线叉乘得到角分面法线
            prev = GetDirToPrevPoint(index);
            next = GetDirToNextPoint(index);
            vec3 midAng = prev + next;
            if(midAng.LengthSq() < _EPSILON)
            {
                if(next.LengthSq() > _EPSILON)
                {
                    midAng = next;
                }
                else
                {
                    midAng = -prev;
                }
            }
            else
            {
                midAng.Normalize();
                midAng = midAng.Cross(GetNormal(index));
                midAng.Normalize();
            }
            point[index].tangent = midAng;
        }
    }
}

float Curve::GetCurveLength()
{
	return m_length;
}

float Curve::Path2Length(float path)
{
	//?非等距点？
	if(-_EPSILON m_knots;
};

BSplineImp::BSplineImp()
{
}

BSplineImp::~BSplineImp()
{
    Free();
}

void BSplineImp::Free()
{
}

#define CUR   m_knots[i]
#define PREV  m_knots[i-1]
#define NEXT  m_knots[i+1]
#define HEAD  m_knots[0]
#define TAIL  m_knots[knotNum-1]


void BSplineImp::PrepareGen(int divNum,bool closed)
{
    Free();
    if(m_knots.size() <= 0)
    {
        return;
    }


	//分段3次Hermite插值曲线：求插值曲线h(x)和原线段f(x) 都过相同控制点，且控制点处切向相同
	//已知线段的两个端点P0、P1和端点处的切线R0、R1
	//q(t) = a*t^3 + b*t^2 + c*t + d

    int knotNum = m_knots.size();
    //Ax 当前控制点线段
    for(int i = 0 ; i <= knotNum - 2 ; i++)
    {
        CUR.Ax = NEXT.pos - CUR.pos;
    }
    if(closed)
    {
        TAIL.Ax = HEAD.pos - TAIL.pos;
    }
    // k 线段比
    float len;
    float lenOld = HEAD.Ax.Length();
    for(int i = 0 ; i <= knotNum - 2 ; i++)
    {
        len = NEXT.Ax.Length();
        CUR.lenRat = lenOld / len;
		//CUR.lenRat = 0.99;
        lenOld = len;
    }
    if(closed)
    {
        //TAIL.lenRat = lenOld / HEAD.Ax.Length();
		TAIL.lenRat = TAIL.Ax.Length() / HEAD.Ax.Length();
    }
    else
    {
        //TAIL.lenRat=1.0f;
        m_knots[knotNum - 2].lenRat = 1.0f;
    }
    // Matrix
    if(closed)
    {
        // Matrix
        for(int i = 1; i <= knotNum - 1; i++)
        {
            CUR.matA = 1.0f;
            CUR.matB = 2.0f * PREV.lenRat * (1.0f + PREV.lenRat);
            CUR.matC = PREV.lenRat * PREV.lenRat * CUR.lenRat;
        }
        HEAD.matA = 1.0f;
        HEAD.matB = 2.0f * TAIL.lenRat * (1.0f + TAIL.lenRat);
        HEAD.matC = TAIL.lenRat * TAIL.lenRat * HEAD.lenRat;
        // Bx
        for(int i = 1; i <= knotNum - 1; i++)
        {
            CUR.Bx = 3.0f * (PREV.Ax + PREV.lenRat * PREV.lenRat * CUR.Ax);
        }
        HEAD.Bx = 3.0f * (TAIL.Ax + TAIL.lenRat * TAIL.lenRat * HEAD.Ax);
        //Bx
        for(int i = 0; i <= knotNum - 1; i++)
        {
            CUR.WorkB = CUR.Work = CUR.Bx / CUR.matB;
        }
        for(int j = 0 ; j < divNum ; j++)
        {
            HEAD.Work = (HEAD.Bx - HEAD.matA * TAIL.WorkB - HEAD.matC * m_knots[1].WorkB)  / HEAD.matB;
            for(int i = 1; i < knotNum - 1 ; i++)
            {
                CUR.Work = (CUR.Bx - CUR.matA * PREV.WorkB - CUR.matC * NEXT.WorkB)  / CUR.matB;
            }
            TAIL.Work = (TAIL.Bx - TAIL.matA * m_knots[knotNum - 2].WorkB - TAIL.matC * HEAD.WorkB) / TAIL.matB;
            for(int i = 0 ; i <= knotNum - 1 ; i++)
            {
                CUR.WorkB = CUR.Work;
            }
        }
        for(int i = 0 ; i <= knotNum - 1 ; i++)
        {
            CUR.Bx = CUR.Work;
        }
    }
    else //open
    {
        // Matrix
        for(int i = 1; i <= knotNum - 2; i++)
        {
            CUR.matA = 1.0f;
            CUR.matB = 2.0f * PREV.lenRat * (1.0f + PREV.lenRat);
            CUR.matC = PREV.lenRat * PREV.lenRat * CUR.lenRat;
        }
        HEAD.matB = 2.0f;
        HEAD.matC = HEAD.lenRat;
        TAIL.matA = 1.0f;
        TAIL.matB = 2.0f * m_knots[knotNum - 2].lenRat;
        // Bx
        for(int i = 1; i <= knotNum - 2; i++)
        {
            CUR.Bx = 3.0f * (PREV.Ax + PREV.lenRat * PREV.lenRat * CUR.Ax);
        }
        HEAD.Bx = 3.0f * HEAD.Ax;
        TAIL.Bx = 3.0f * m_knots[knotNum - 2].Ax;
        //Bx
        for(int i = 0; i <= knotNum - 1; i++)
        {
            CUR.WorkB = CUR.Work = CUR.Bx / CUR.matB;
        }
        for(int j = 0 ; j < divNum ; j++)
        {
            HEAD.Work = (HEAD.Bx - HEAD.matC * m_knots[1].WorkB)  / HEAD.matB;
            for(int i = 1; i < knotNum - 1 ; i++)
            {
                CUR.Work = (CUR.Bx - CUR.matA * PREV.WorkB - CUR.matC * NEXT.WorkB) / CUR.matB;
            }
            TAIL.Work = (TAIL.Bx - TAIL.matA * m_knots[knotNum - 2].WorkB) / TAIL.matB;
            for(int i = 0 ; i <= knotNum - 1 ; i++)
            {
                CUR.WorkB = CUR.Work;
            }
        }
        for(int i = 0 ; i <= knotNum - 1 ; i++)
        {
            CUR.Bx = CUR.Work;
        }
    }
    //Cx
    for(int i = 0 ; i <= knotNum - 2 ; i++)
    {
        CUR.Cx = CUR.lenRat * NEXT.Bx;
    }
    if(closed)
    {
        TAIL.Cx = TAIL.lenRat * HEAD.Bx;
    }
}

void BSplineImp::GenSmoothPoints(Curve*curve,int divNum,bool closed)
{
    curve->Clear();
	curve->SetClosed(closed);
    int knotNum = m_knots.size();
	//float DivLen = 20; 
	vec3  pos;
	float t, f, g, h;
    for(int i = 0; i < knotNum - 1 ; i++)
    {
        //计算当前控制点和下个控制点之间的部分
        vec3& start = CUR.pos;
        vec3& Ax = CUR.Ax;
        vec3& Bx = CUR.Bx;
        vec3& Cx = CUR.Cx;
        curve->AddPoint(start);
        //divNum = CUR.Ax.Length() /DivLen ;
       // if(divNum <= 0)divNum = 1;
        for(int i = 1; i < divNum ; i++)
        {
            t = 1.0f / (float)divNum * (float)i;//0~0.9
            f = t * t * (3.0f - 2.0f * t);      //f = -2t^3  + 3t^2
            g = t * (t - 1.0f) * (t - 1.0f);    //g =   t^3  - 2t^2  + t
            h = t * t * (t - 1.0f);             //h =   t^3  - t^2
            pos = (start + Ax * f + Bx * g + Cx * h);
            curve->AddPoint(pos);
        }
    }
	if (closed)
	{
		//
		vec3& start = TAIL.pos;
		vec3& Ax = TAIL.Ax;
		vec3& Bx = TAIL.Bx;
		vec3& Cx = TAIL.Cx;
		curve->AddPoint(start);
		//divNum = CUR.Ax.Length() /DivLen ;
		//if(divNum <= 0)divNum = 1;
		for(int i = 1; i < divNum ; i++)
		{
			t = 1.0f / (float)divNum * (float)i;//0~0.9
			f = t * t * (3.0f - 2.0f * t);      //f = -2t^3  + 3t^2
			g = t * (t - 1.0f) * (t - 1.0f);    //g =   t^3  - 2t^2  + t
			h = t * t * (t - 1.0f);             //h =   t^3  - t^2
			pos = (start + Ax * f + Bx * g + Cx * h);
			curve->AddPoint(pos);
		}
		//curve->AddPoint(HEAD.pos);
	}
	else
	{
		curve->AddPoint(TAIL.pos);
	}
    curve->Update();
}


//==================^_^==================^_^==================^_^==================^_^
BSpline::BSpline()
{
    m_splineImp = new BSplineImp;
}

BSpline::BSpline(const vec3* knots, int size,int divNum)
{
    m_splineImp = new BSplineImp;
    if(size >= 0)
    {
        m_splineImp->m_knots.resize(size);
    }
    if(knots)
    {
        for(int i = 0; i < size; i++)
        {
            m_splineImp->m_knots[i].pos = knots[i];
        }
    }
    GenSmoothPoints(divNum);
}

BSpline::~BSpline()
{
    m_splineImp->m_knots.clear();
    if(m_splineImp)
    {
        delete m_splineImp;
        m_splineImp = NULL;
    }
}

void BSpline::Clear()
{
    Curve::Clear();
    m_splineImp->m_knots.clear();
}
void BSpline::operator=(const BSpline& curve)
{
    //Curve::operator= curve;
}

void BSpline::Render(int opt)
{
    Curve::Render(opt);
    G_RendDriver->SetRenderStateEnable(RS_TEXTURE_2D, false);
	//绘制控制点
    if(1)
    {
        G_RendDriver->SetPointSize(4);
        G_RendDriver->Color3f(1.0f, 0.0f, 0.0f);
        G_RendDriver->RendBegin(RS_POINTS);
        int knotNum = m_splineImp->m_knots.size();
        Knot* knot  = &m_splineImp->m_knots[0];
        vec3 pos;
        for(int i = 0; i < knotNum; i++)
        {
            pos = knot[i].pos;
            G_RendDriver->Vertex3fv(&pos.x);
        }
        G_RendDriver->RendEnd();
    }
	//绘制控制点的连线
	if(opt&4)
    {
        G_RendDriver->Color3f(0.0f, 1.0f, 0.0f);
        G_RendDriver->RendBegin(RS_LINES);
        int knotNum = m_splineImp->m_knots.size();
        Knot* knot  = &m_splineImp->m_knots[0];
        vec3 pos;
        for(int i = 0; i < knotNum; i++)
        {
            pos = knot[i].pos;
            G_RendDriver->Vertex3fv(&pos.x);
            G_RendDriver->Vertex3fv(&pos.x);
        }
        G_RendDriver->RendEnd();
    }
    //G_RendDriver->SetRenderStateEnable(RS_LIGHTING,true);
    G_RendDriver->SetRenderStateEnable(RS_TEXTURE_2D, true);
    G_RendDriver->Color3f(1.0f, 1.0f, 1.0f);
}

bool BSpline::GenSmoothPoints(int divNum)
{
	//m_isClosed = true;
    m_splineImp->PrepareGen(divNum,m_isClosed);
    m_splineImp->GenSmoothPoints(this,divNum,m_isClosed);
    return true;
}
int  BSpline::GetKnotNum() const
{
    return m_splineImp->m_knots.size();
}
void BSpline::AddKnot(const vec3& point)
{
    Knot v;
    v.pos = point;
    m_splineImp->m_knots.push_back(v);
}

void BSpline::AddKnot(const Knot& v)
{
    m_splineImp->m_knots.push_back(v);
}

void BSpline::DelKnot(int index)
{
}
BSpline::Knot* BSpline::GetKnot(int index)
{
    if(index < 0 || index >= m_splineImp->m_knots.size())
        return NULL;
    return &m_splineImp->m_knots[index];
}



//==================^_^==================^_^==================^_^==================^_^
class HSplineImp
{
public:
	HSplineImp();
	~HSplineImp();
	void Free();
	void GenSmoothPoints(Curve*curve,int divNum,bool closed);

public:
	std::vector m_knots;
};

HSplineImp::HSplineImp()
{
}

HSplineImp::~HSplineImp()
{
	Free();
}

void HSplineImp::Free()
{
}

class Hermite3
{
public:
	//分段3次Hermite插值曲线：求插值曲线h(x)和原线段f(x) 都过相同控制点，且控制点处切向相同
	//已知线段的两个端点P0、P1和端点处的切线R0、R1
	//q(t) = a*t^3 + b*t^2 + c*t + d

	vec3 p1;             //control point         
	vec3 p2;                  
	vec3 tp1;            //tangent point
	vec3 tp2;             
	vec3 tan1;           //tangent vector
	vec3 tan2;          
	float weight;      // artificial weight applied to tangent direction - weights curve more in direction of tangent

	Hermite3()
	{
		weight = 3.0;
	}

	//切线控制点
	void SetTangentKnot(const vec3& p1, const vec3& p2)
	{
		tp1   = p1;
		tan1  = tp1 - this->p1;
		tp2   = p2;
		tan2  = tp2 - this->p2;
	}

	//曲线控制点
	void SetKnot(const vec3& p1, const vec3& p2)
	{
		this->p1   = p1; 
		tan1 = tp1 - p1;
		this->p2   = p2;
		tan2 = tp2 - p2;
	}

	// t [0,1]
	void GetPos(float t,vec3& pos)
	{
		t = (t<0) ? 0 : t;
		t = (t>1) ? 1 : t;
		float t2 = t*t;
		float t3 = t2*t;

		//float C1 =  2.0*t3 - 3.0*t2 + 1.0;
		//float C2 = -2.0*t3 + 3.0*t2;
		//float C3 =      t3 - 2.0*t2 + t;
		//float C4 =      t3 -     t2;

		//todo：预计算divNum个值
		float C2 = -2.0*t3 + 3.0*t2;
		float C1 = 1.0 - C2;
		float C4 = t3 - t2;
		float C3 = t + C4 - t2;

		pos = (p1*C1 + p2*C2 + (tan1*C3 + tan2*C4)*weight);
	}

};

void HSplineImp::GenSmoothPoints(Curve*curve,int divNum,bool closed)
{
	Hermite3 seg;

	curve->Clear();
	curve->SetClosed(closed);
	int knotNum = m_knots.size();
	//float DivLen = 20; 
	vec3  pos;
	float t;
	for(int i = 0; i < knotNum - 1 ; i++)
	{
		//计算当前控制点和下个控制点之间的部分
		vec3& start = CUR.pos;

		seg.SetKnot(CUR.pos,NEXT.pos);
		seg.SetTangentKnot(CUR.tanPos2, NEXT.tanPos1-NEXT.tanVec1*2);

		curve->AddPoint(start);
		//divNum = CUR.Ax.Length() /DivLen ;
		// if(divNum <= 0)divNum = 1;
		for(int i = 1; i < divNum ; i++)
		{
			t = 1.0f / (float)divNum * (float)i;//0~0.9
			seg.GetPos(t,pos);
			curve->AddPoint(pos);
		}
	}
	if (closed)
	{
		//
		vec3& start = TAIL.pos;

		seg.SetKnot(TAIL.pos,HEAD.pos);
		seg.SetTangentKnot(TAIL.tanPos2,HEAD.tanPos1-HEAD.tanVec1*2);

		curve->AddPoint(start);
		//divNum = CUR.Ax.Length() /DivLen ;
		//if(divNum <= 0)divNum = 1;
		for(int i = 1; i < divNum ; i++)
		{
			t = 1.0f / (float)divNum * (float)i;//0~0.9
			seg.GetPos(t,pos);
			curve->AddPoint(pos);
		}
		//curve->AddPoint(HEAD.pos);
	}
	else
	{
		curve->AddPoint(TAIL.pos);
	}
	curve->Update();
}


//==================^_^==================^_^==================^_^==================^_^
HSpline::HSpline()
{
	m_splineImp = new HSplineImp;
}

HSpline::HSpline(const vec3* knots, int size,int divNum)
{
	m_splineImp = new HSplineImp;
	if(size >= 0)
	{
		m_splineImp->m_knots.resize(size);
	}
	if(knots)
	{
		for(int i = 0; i < size; i++)
		{
			m_splineImp->m_knots[i].pos = knots[i];
		}
	}
	GenSmoothPoints(divNum);
}

HSpline::~HSpline()
{
	m_splineImp->m_knots.clear();
	if(m_splineImp)
	{
		delete m_splineImp;
		m_splineImp = NULL;
	}
}

void HSpline::Clear()
{
	Curve::Clear();
	m_splineImp->m_knots.clear();
}
void HSpline::operator=(const HSpline& curve)
{
	//Curve::operator= curve;
}

void HSpline::Render(int opt)
{
	Curve::Render(opt);
	G_RendDriver->SetRenderStateEnable(RS_TEXTURE_2D, false);
	//绘制控制点 控制柄
	if(1)
	{
		G_RendDriver->SetPointSize(4);
		G_RendDriver->Color3f(1.0f, 0.0f, 0.0f);
		G_RendDriver->RendBegin(RS_POINTS);
		int knotNum = m_splineImp->m_knots.size();
		Knot* knot  = &m_splineImp->m_knots[0];
		vec3 pos;
		for(int i = 0; i < knotNum; i++)
		{
			//控制点
			G_RendDriver->Color3f(1.0f, 0.0f, 0.0f);
			pos = knot[i].pos;
			G_RendDriver->Vertex3fv(&pos.x);
			//控制柄点
			G_RendDriver->Color3f(1.0f, 0.0f, 1.0f);
			pos = knot[i].tanPos1;
			G_RendDriver->Vertex3fv(&pos.x);
			G_RendDriver->Color3f(0.0f, 0.0f, 1.0f);
			pos = knot[i].tanPos2;
			G_RendDriver->Vertex3fv(&pos.x);
		}
		G_RendDriver->RendEnd();
	}
	//控制柄线
	if(1)
	{
		G_RendDriver->Color3f(0.0f, 1.0f, 0.0f);
		G_RendDriver->RendBegin(RS_LINES);
		int knotNum = m_splineImp->m_knots.size();
		Knot* knot  = &m_splineImp->m_knots[0];
		vec3 pos;
		for(int i = 0; i < knotNum; i++)
		{
			pos = knot[i].pos;
			G_RendDriver->Vertex3fv(&pos.x);
			pos = knot[i].tanPos1;
			G_RendDriver->Vertex3fv(&pos.x);
			pos = knot[i].pos;
			G_RendDriver->Vertex3fv(&pos.x);
			pos = knot[i].tanPos2;
			G_RendDriver->Vertex3fv(&pos.x);
		}
		G_RendDriver->RendEnd();
	}
	//G_RendDriver->SetRenderStateEnable(RS_LIGHTING,true);
	G_RendDriver->SetRenderStateEnable(RS_TEXTURE_2D, true);
	G_RendDriver->Color3f(1.0f, 1.0f, 1.0f);
}

bool HSpline::GenSmoothPoints(int divNum)
{
	//m_isClosed = true;
	m_splineImp->GenSmoothPoints(this,divNum,m_isClosed);
	return true;
}
int  HSpline::GetKnotNum() const
{
	return m_splineImp->m_knots.size();
}
void HSpline::AddKnot(const vec3& newPos)
{
	Knot vNew;
	vNew.pos = newPos;
	vec3 newVec;
	vec3 preVec;

#define Lerp_ 0.5f
//#define Lerp_ 0.6f

	int knotNum = m_splineImp->m_knots.size();
	if (knotNum > 0)
	{
		Knot* back = &m_splineImp->m_knots.back();
		//新加点 控制柄沿直线
		newVec = (newPos - back->pos)*0.2f;

		if (knotNum==1)
		{
			back->tanVec1 = -newVec;//控制柄相同
			back->tanVec2 = newVec;
			back->tanPos1 = back->pos + back->tanVec1;
			back->tanPos2 = back->pos + back->tanVec2;
		}
		else
		{
			//前点控制柄旋转
			Knot* prev = back-1;
			preVec = (back->pos - prev->pos)*0.2f;

			back->tanVec2 = (preVec + newVec)*Lerp_;
			back->tanPos2 = back->pos + back->tanVec2;
			back->tanVec1 = -back->tanVec2;
			back->tanPos1 = back->pos + back->tanVec1;

			if(m_isClosed == false)
			{
				vNew.tanVec1 = -newVec;
				vNew.tanPos1 = newPos + vNew.tanVec1;
				vNew.tanVec2 = newVec;
				vNew.tanPos2 = newPos + vNew.tanVec2;
			}
			else
			{
				Knot* head = &m_splineImp->m_knots.front();

				preVec = newVec;
				newVec = (head->pos - newPos)*0.2f;
				vNew.tanVec2 = (preVec + newVec)*Lerp_;
				vNew.tanPos2 = vNew.pos + vNew.tanVec2;
				vNew.tanVec1 = -vNew.tanVec2;
				vNew.tanPos1 = vNew.pos + vNew.tanVec1;

				preVec = newVec;
				newVec = ((head+1)->pos - head->pos)*0.2f;
				head->tanVec2 = (preVec + newVec)*Lerp_;
				head->tanPos2 = head->pos + head->tanVec2;
				head->tanVec1 = -head->tanVec2;
				head->tanPos1 = head->pos + head->tanVec1;
			}
		}
	}
	m_splineImp->m_knots.push_back(vNew);
}

void HSpline::AddKnot(const Knot& v)
{
	m_splineImp->m_knots.push_back(v);
}

void HSpline::DelKnot(int index)
{
}
HSpline::Knot* HSpline::GetKnot(int index)
{
	if(index < 0 || index >= m_splineImp->m_knots.size())
		return NULL;
	return &m_splineImp->m_knots[index];
}