吴恩达机器学习正则化Logistic算法与神经网络的MATLAB实现(对应ex3练习)
前言:本次作业主要是一个多分类案例的实现。其主要是利用logistic算法,多分类与二分类问题相似。其主要思想是将N类别的分类转换成N个二分类问题,每次选择其中一个类别作为正类,其余的类别都作为反类,计算出相应的权重。最后通过计算出来的N个权重对输入样本做预测,选取其中最大输出作为最终的输出。
lrCostFunction.m
该函数是正则化logistic算法的实现,包括计算代价函数和梯度,值得注意的就是在正则化过程中并未对第一列常量1进行正则化。在代码中同时贴出了循环实现的梯度计算和向量化实现的梯度计算。对于循环实现的梯度计算更利于理解,但是运行较慢,向量化实现梯度计算速度较快。
这里值得注意的有两点:1、在计算J(θ)时,注意后面的累加项的j是从1开始的,也就是说并没有累加第一项0。这点在吴恩达的授课视频中也专门指出来过。在用MATLAB实现时,由于其中序号是从1开始的 ,所以在累加时应该从2开始;2、在计算j≥1时的梯度时,同样的不能把第0项(MATLAB中是第1项)加进来。下面附实现代码,其中的theta(2:end,:)意思就是抛弃第1项。
function [J, grad] = lrCostFunction(theta, X, y, lambda)
%LRCOSTFUNCTION Compute cost and gradient for logistic regression with
%regularization
% J = LRCOSTFUNCTION(theta, X, y, lambda) computes the cost of using
% theta as the parameter for regularized logistic regression and the
% gradient of the cost w.r.t. to the parameters.
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
grad = zeros(size(theta));
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
% You should set J to the cost.
% Compute the partial derivatives and set grad to the partial
% derivatives of the cost w.r.t. each parameter in theta
%
% Hint: The computation of the cost function and gradients can be
% efficiently vectorized. For example, consider the computation
%
% sigmoid(X * theta)
%
% Each row of the resulting matrix will contain the value of the
% prediction for that example. You can make use of this to vectorize
% the cost function and gradient computations.
%
% Hint: When computing the gradient of the regularized cost function,
% there're many possible vectorized solutions, but one solution
% looks like:
% grad = (unregularized gradient for logistic regression)
% temp = theta;
% temp(1) = 0; % because we don't add anything for j = 0
% grad = grad + YOUR_CODE_HERE (using the temp variable)
%
% theta 4*1;X 5*4;y 5*1;lambda 3
h = sigmoid(X * theta);
J = -m ^ -1 * sum(y .* log(h) + (1 - y) .* log(1 - h)) + lambda * sum(theta(2:end,:) .^ 2) / (2 * m);
grad(1,:) = m ^ -1 * sum((h - y) .* X(:,1));
%% 向量化求解
grad(2:end,:) = m ^ -1 * X(:,2:end)' * (h - y) + m ^ -1 * lambda * theta(2:end,:);
%% 循环求解
% for i = 2 : size(theta,1);
% grad(i,:) = m ^ -1 * sum((h - y) .* X(:,i)) + lambda / m * theta(i,:);
% end
% =============================================================
end
oneVsAll.m
这个函数的功能是实现对权重参数的求解。因为要对0~9十个样本进行分类,按照logistic算法多分类的思想应该有10个向量参数。其具体实现是每次将其中一个样本作为正例,其余作为反例,这样循环十次即可求出参数向量。
function [all_theta] = oneVsAll(X, y, num_labels, lambda)
%ONEVSALL trains multiple logistic regression classifiers and returns all
%the classifiers in a matrix all_theta, where the i-th row of all_theta
%corresponds to the classifier for label i
% [all_theta] = ONEVSALL(X, y, num_labels, lambda) trains num_labels
% logistic regression classifiers and returns each of these classifiers
% in a matrix all_theta, where the i-th row of all_theta corresponds
% to the classifier for label i
% Some useful variables
m = size(X, 1);
n = size(X, 2);
% You need to return the following variables correctly
all_theta = zeros(num_labels, n + 1);%10 * 401
% Add ones to the X data matrix
X = [ones(m, 1) X];%5000 * 401
% ====================== YOUR CODE HERE ======================
% Instructions: You should complete the following code to train num_labels
% logistic regression classifiers with regularization
% parameter lambda.
%
% Hint: theta(:) will return a column vector.
%
% Hint: You can use y == c to obtain a vector of 1's and 0's that tell you
% whether the ground truth is true/false for this class.
%
% Note: For this assignment, we recommend using fmincg to optimize the cost
% function. It is okay to use a for-loop (for c = 1:num_labels) to
% loop over the different classes.
%
% fmincg works similarly to fminunc, but is more efficient when we
% are dealing with large number of parameters.
%
% Example Code for fmincg:
%
% % Set Initial theta
% initial_theta = zeros(n + 1, 1);
%
% % Set options for fminunc
% options = optimset('GradObj', 'on', 'MaxIter', 50);
%
% % Run fmincg to obtain the optimal theta
% % This function will return theta and the cost
% [theta] = ...
% fmincg (@(t)(lrCostFunction(t, X, (y == c), lambda)), ...
% initial_theta, options);
%
% X 5000 * 400;Y 5000 * 1;num_labels 10;lambda 0.1
options = optimset('GradObj','on','MaxIter',50);
for i = 1 : 10;
initial_theta = zeros(n + 1, 1);
all_theta(i,:) = fmincg(@(t)lrCostFunction(t, X, (y == i), lambda),initial_theta,options);
end
% =========================================================================
endpredictOneVsAll.m
这个函数的功能是实现对样本的预测,具体思路是将样本特征与求解出来的参数向量作乘,因为有十个参量,因此每个样本对应有十个输出值。最后,我们选择十个输出值中最大的值最为最终的预测。
function p = predictOneVsAll(all_theta, X)
%PREDICT Predict the label for a trained one-vs-all classifier. The labels
%are in the range 1..K, where K = size(all_theta, 1).
% p = PREDICTONEVSALL(all_theta, X) will return a vector of predictions
% for each example in the matrix X. Note that X contains the examples in
% rows. all_theta is a matrix where the i-th row is a trained logistic
% regression theta vector for the i-th class. You should set p to a vector
% of values from 1..K (e.g., p = [1; 3; 1; 2] predicts classes 1, 3, 1, 2
% for 4 examples)
m = size(X, 1);%5000
% You need to return the following variables correctly
p = zeros(size(X, 1), 1);%5000*1
% Add ones to the X data matrix
X = [ones(m, 1) X];%5000 * 401
% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
% your learned logistic regression parameters (one-vs-all).
% You should set p to a vector of predictions (from 1 to
% num_labels).
%
% Hint: This code can be done all vectorized using the max function.
% In particular, the max function can also return the index of the
% max element, for more information see 'help max'. If your examples
% are in rows, then, you can use max(A, [], 2) to obtain the max
% for each row.
%
h=sigmoid( X*all_theta');%5000 * 10 每个输入对应1-10之间的概率 选取其中概率最大的作为预测结果
[~,col_num]=max(h,[],2); %求出每行最大的值所在的序号
p = col_num;
% =========================================================================
endpredict.m
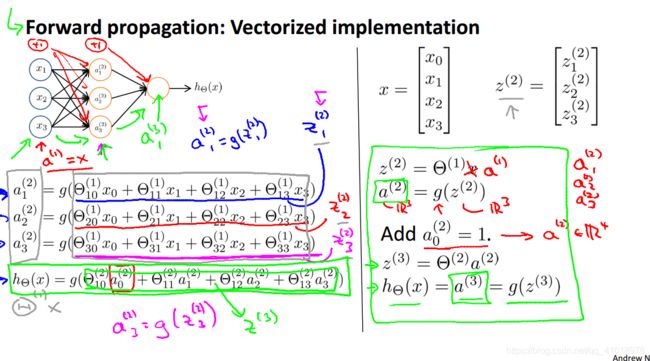
这个函数是使用神经网络来做预测,对于一个输入经过三层神经网络:输入层、隐藏层、输出层后输出结果。该函数的重要点是理解神经网络前向传播的特点,下图给出了课件上神经网络传播的方式。自己跟着推导一下理解即可。
神经网络前向传播实现的的注意点是需要在给除了输出层外的每一层添加偏差单元,在下面的代码中分别使用循环和向量化的方式实现神经网络的前向传播。
function p = predict(Theta1, Theta2, X)
%PREDICT Predict the label of an input given a trained neural network
% p = PREDICT(Theta1, Theta2, X) outputs the predicted label of X given the
% trained weights of a neural network (Theta1, Theta2)
% Useful values
m = size(X, 1);
% You need to return the following variables correctly
p = zeros(size(X, 1), 1);
% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
% your learned neural network. You should set p to a
% vector containing labels between 1 to num_labels.
%
% Hint: The max function might come in useful. In particular, the max
% function can also return the index of the max element, for more
% information see 'help max'. If your examples are in rows, then, you
% can use max(A, [], 2) to obtain the max for each row.
%
% =========================================================================
a1 = [ones(m,1) X];%给输入层添加偏差单元
%% 循环的方式实现前向传播算法
% for i = 1 : m;
% z1 = Theta1 * a1(i,:)';
% a2 = sigmoid(z1);
% z2 = Theta2 * [1;a2];%添加偏差单元
% [~,id] = max(sigmoid(z2));%取值最大的输出的序号
% p(i,:) = id;
% end
%% 向量化的方式实现
z1 = a1 * Theta1';
a2 = [ones(size(z1,1),1) sigmoid(z1)];%添加偏差单元
z2 = a2 * Theta2';
resMat = sigmoid(z2);
[~,p] = max(resMat,[],2);
end