AAAI2023 | 均匀序列更好：时间间隔感知的序列推荐数据增强方法

文章信息

来源：AAAI 2023
标题：Uniform Sequence Better: Time Interval Aware Data Augmentation for Sequential Recommendation
机构：东北大学软件学院 阿里巴巴
作者：Yizhou Dang, Enneng Yang, Guibing Guo, Linying Jiang, Xingwei Wang, Xiaoxiao Xu, Qinghui Sun, Hong Liu
链接：https://arxiv.org/abs/2212.08262
代码：https://github.com/KingGugu/TiCoSeRec

内容简介

序列推荐已经成为一项重要的推荐任务，根据用户的历史交互序列预测下一个时间点用户访问的项目。作者发现序列中两个项目交互的时间间隔并没有得到广泛的关注，特别是考虑到兴趣偏移时。图1是从真实数据集中抽取的一个例子。两个用户拥有相同长度的交互序列，但他们交互间隔的分布却相差很多。用户1的时间间隔分布相对用户2更为均匀。用户1购买的大多数产品都属于皮肤/面部护理类别，而用户2购买的产品类别却随着时间发生了较大的改变（从发胶到睫毛膏，从睫毛膏到保湿霜）。直观地认为，由于用户1的序列比其他用户分布更均匀，因此模型可以更好地学习用户偏好。作者将用户1这种序列称为“均匀序列”，用户2称为“非均匀序列”。
​
在本文中，作者进行了实证研究来进一步验证这一猜想。实验结果表明，均匀序列比非均匀序列可以显著提高模型性能，然而，真实数据集中序列在时间间隔上不能均匀分布是一个很普遍的现象。基于实证研究的结果，作者提出了五个时间间隔感知的数据增强算子（Ti-Crop, Ti-Reorder, Ti-Mask, TiSubstitute, Ti-Insert）来将非均匀序列转换为均匀序列。此外，作者应用对比学习来确保增强序列与原始序列保持较高的相似性。作者在一个最先进推荐模型CoSeRec上实现了作者的方法，并提出了TiCoSeRec。

本文的主要贡献有：
1.作者进行了实证研究来验证均匀序列比非均匀序列更有利于模型性能提升。据作者所知，这是第一个对序列推荐时间间隔分布的研究。
2.作者提出了5个数据增强算子，将非均匀序列转换为均匀序列，此外，作者还设计了一种控制策略来处理短序列的数据增强。
3.作者在4个真实数据集上进行了广泛的实验，并证明了与其他11个竞争模型相比，作者的方法TiCoSeRec可以实现显著的性能提高。

实证研究

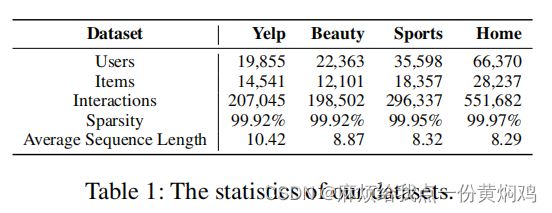
本文所有的实验均在表1中展示的四个数据集上进行。在本文中，作者用序列时间间隔的标准差来判定序列是否均匀。如果一个序列的时间间隔的标准差较小，那么它为均匀序列，如果时间间隔的标准差较大，那么它为非均匀序列。作者计算了数据集中所有序列时间间隔的标准差。作者通过设置不同的标准差阈值来分析数据集中均匀（非均匀）序列的数量，结果如图2所示。
​
横轴表示门槛值。这里门槛值是数据集中所有序列标准差的均值的比率（例如0.5表示门槛为标准差均值×0.5）。序列的标准差小于门槛值即为均匀序列，大于门槛值即为非均匀序列。纵轴表示此时均匀序列的百分比。总的来说非均匀序列占据了总体数据的很大一部分（40-50%）。
之后，作者对每个数据集的所有序列按时间间隔的标准差由小到大进行排名。采取了三种不同的划分方式。U为均匀子集，N为非均匀子集。三种策略分别是：

• 1.按用户划分（S）：排名前50%用户一个子集（S:U），后50%一个子集（S:N）。两个子集用户数相同，但交互数不同。
• 2.按交互数量划分（I）：排名前50%的交互一个子集（I:U），后50%一个子集（I:U）。两个子集交互数相同，用户数不同。
• 3.从数据集中随机抽取50%的序列（Random）。
  之后对比四个模型在不同子集上的表现。结果如表2所示。可以看出模型在均匀子集上的表现普遍好于非均匀子集。且随机子集的结果在均匀子集与非均匀子集中间，即非均匀＜随机＜均匀。
  ​

方法介绍

作者将序列排序的前σ比率标记为均匀的序列，其余标记为非均匀的序列，需要增强以提高更好的性能。假设作者总共有m个项目序列，那么就有m（1−σ）的项目序列作为非均匀序列。图3对比了作者时间间隔感知的算子与传统算子的不同之处。图中也对比了操作前后序列时间间隔的标准差。标准差减少，说明序列均匀程度提高。
​
Ti-Insert：给定序列长度N和插入率β，那么插入项目的数量就是k=Nβ。传统的Insert算子会随机选择k个位置插入物品。Ti-Insert会对序列中所有的时间间隔从大到小进行排序，并选择排序中Top-k个时间间隔进行插入。通过向较大的时间间隔插入物品，可以使用户的兴趣过渡更为平滑。

Ti-Crop：给定序列长度N和裁切率η，那么裁切得到的子序列长度c=Nη。传统的Crop算子会随机选择一个位置裁切得到子序列。Ti-Crop会计算所有可能的子序列的时间间隔的标准差，并从中选出标准差最小的子序列。

Ti-Mask：给定序列长度N和遮盖率µ，那么遮盖项目的数量就是k=Nµ。传统的Mask算子会随机选择k个位置进行遮盖。Ti-Mask会对序列中所有的时间间隔从小到大进行排序，并选择排序中Top-k个时间间隔进行遮盖。如果遮盖掉大时间间隔周围物品，会使原本的间隔进一步扩大，从而使得序列更为不均匀。Ti-Mask对小时间间隔周围物品进行遮盖，使序列在整体上更为均匀。

Ti-Substitute：Ti-Substitute与Ti-Mask类似，只不过Ti-Substitute是用相似项目替代原始项目。在图3(e)中，传统的Substitute很有可能对关键项目（如项目v6和v7）进行替换，导致模型不能很好地捕获用户偏好的变化。相比之下，Ti-Substitute专注于时间间隔较小的项目，新序列更容易保持与原始序列相似的偏好模式。简单来说，该算子将通过对原始序列施加最小的变化（通过替换）来获得新的序列。

Ti-Reorder：与Ti-Crop相似，Ti-Reorder会对选择出的标准差小的子序列。新生成的序列与原始序列长度相同，只不过对部分项目进行了shuffle。传统的Reorder在选择shuffle位置时是随机的，这可能会破坏原始序列的偏好模式。由于Ti-Crop会选择标准差最小的子序列，因此在数据重新排序后，它有较高的机会保持相似的偏好模式。例如，作者在图3(f)中得到了一个新的类别模式是B→B→B→C，它与原来的类别模式相似。

因为短序列对于裁切和遮盖更为敏感，所以参考CoSeRec，作者对不同长度的序列应用不同的数据增强算子，如公式5所示。N为序列长度，K为区分长短序列的阈值。Su为算子集。每次数据增强时会从算子集中随机抽取两个进行数据增强，生成两个增强序列用于对比学习。

实验分析

整体表现

作者继续在实证研究的四个数据集上进行实验。对比的模型主要分为三个类别，包括非序列模型、序列模型和包含数据增强方法的序列模型。表3显示了不同方法在推荐任务上的性能。最好的结果用粗体表示，第二好的结果用斜体表示，Improve表示相对于最佳基线的改进百分比。

可以观察到，作者提出的TiCoSeRec方法在所有数据集上始终表现最好，相对改进百分比范围从5%到18%。与CoSeRec相比，这些改进可能更显著，因为作者在进行数据增强时考虑到了时间间隔的影响。作者的数据增强不仅可以将非均匀序列转化为均匀序列，而且还可以保证新生成的序列与原始序列具有很高的相似性。

消融实验

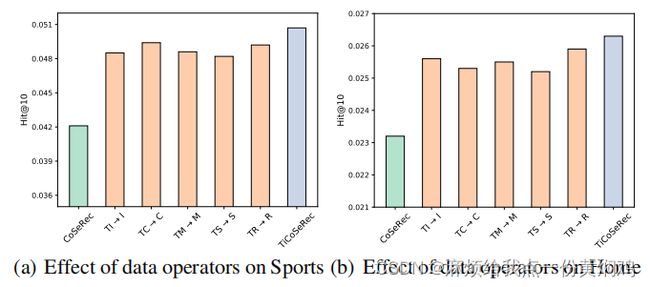
在消融实验中，作者对每个算子对模型表现的贡献进行了研究(a)(b)。具体来说，作者每次都用相应的原始数据增强算子（例如TR→R）替换对应的时间间隔感知算子，并将其他算子保持不变。当将作者所提出的数据增强算子被替换为原始算子时，推荐精度将会下降，这表明了作者所提出的算子的有效性。在所有的变体中，TS→S的性能最差，而TR→R的表现最好。换句话说，TS算子对推荐性能的影响最大，而TR算子的影响最小。

作者也研究了参数σ的影响(c)，该参数控制被视为均匀序列的比率，这个参数越小（即数据集中被视为均匀序列的数量越少，非均匀序列越多），需要增强序列就越多。四个数据集的结果遵循相似的趋势。也就是说，随着σ的提高，性能逐渐提高，然后在设置为0.2或0.3时达到最大值。一般来说，σ=0.2的性能最好。换句话说，最好将排名前20%的序列看作是均匀的，而其余的则需要进行增强，以获得更好的准确性。进一步增加σ的值不会在更大程度上提高性能。总之，一个正确的参数σ的设置对于推荐是很重要的。

结论

本文探讨了时间间隔对序列推荐的影响。作者的核心思想是均匀序列对于模型学习和预测用户偏好更具价值，这一假设在实证研究中得到验证。之后，作者提出了五种时间间隔感知的数据增强算子来增强序列。作者在四个公开数据集上的实验验证了作者提出的算子的有效性。据作者所知，这是第一个研究序列推荐中数据时间间隔分布的工作。作者希望这项工作可以为序列推荐任务中的时间序列建模提供一个新的视角。对于未来的工作，作者打算进一步考虑项目类别的因素来进行数据增强，以及如何将时间间隔和项目类别结合起来以获得更好的性能。