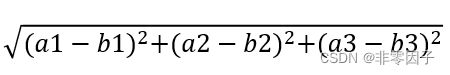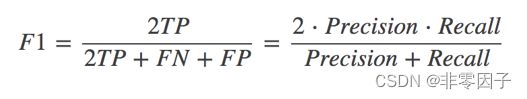机器学习——分类算法之K近邻+朴素贝叶斯,模型选择与调优
目录
K-近邻算法
定义
如何求距离?
数据预处理——标准化
sklearn k-近邻算法API
案例——预测入住位置
分类问题
数据处理
k近邻算法相关问题
k值取多大?有什么影响?
优缺点
应用场景
案例——鸢尾花分类
朴素贝叶斯算法
概率基础
联合概率和条件概率
朴素贝叶斯——贝叶斯公式
拉普拉斯平滑系数
sklearn朴素贝叶斯实现API
案例——20类新闻文本分类
朴素贝叶斯分类的优缺点
分类模型的评估
混淆矩阵
精确率(Precision)与召回率(Recall)以及F1-score
分类模型评估API
模型的选择与调优
交叉验证——n折
网格搜索——调参数
超参数搜索-网格搜索API
![]()
K-近邻算法
定义
如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。——计算欧式距离,根据离你最近的邻居判断你的类别
如何求距离?
两个样本的距离可以通过如下公式计算,又叫欧式距离——计算特征之间的距离
比如说,a(a1,a2,a3),b(b1,b2,b3)
相似的样本,特征之间的值应该都是相近的
数据预处理——标准化
结合我们之前讲的约会数据例子,在计算两个样本数据的距离时特征有什么影响?需要对数据做些什么?
k近邻算法:需要做标准化处理
标准化之前
预测的准确率为: 0.029787234042553193标准化之后
预测的准确率为: 0.41300236406619384sklearn k-近邻算法API
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')
- n_neighbors:int,可选(默认= 5),k_neighbors查询默认使用的邻居数
- algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},可选用于计算最近邻居的算法:‘ball_tree’将会使用 BallTree,‘kd_tree’将使用 KDTree。‘auto’将尝试根据传递给fit方法的值来决定最合适的算法。 (不同实现方式影响效率)
案例——预测入住位置
Facebook V: Predicting Check Ins | Kaggle
In this competition, you are going to predict which business a user is checking into based on their location, accuracy, and timestamp.
分类问题
- 特征值:x\y坐标,定位准确性,时间戳,+日,时,周
- 目标值:入住位置的id
数据处理
- 由于数据量太大,为节省时间,可以缩小x\y,0
- 时间戳进行处理(年,月,日,周,时分秒),当作新的特征
- 几千~几万入住位置,少于一定签到用户的可以删除
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import pandas as pd
def knn_fen():
"""
K-近邻预测用户签到位置
:return:
"""
# 读取数据
data = pd.read_csv('./案例/02-facebookpredicting/train.csv')
# 处理数据
# 1、缩小数据,查询数据筛选
data = data.query('x>1.0 & x<1.25 & y>2.5 & y<2.75')
# 2、处理时间数据,数字变成 年月日时分秒,1970-01-01 10:33:56
time_value = pd.to_datetime(data['time'],unit='s')
# 3、把日期格式转换成 字典格式,1970-01-01 10:33:56 变成(['1970-01-01 18:09:40'])
time_value = pd.DatetimeIndex(time_value)
# 4、构造一些新特征
data.loc[:,('day')] = time_value.day
data.loc[:,('hour')] = time_value.hour
data.loc[:,('weekday')] = time_value.weekday
# 5、把时间戳特征删除,1是列,0是行
data = data.drop(['time'],axis=1)
# 6、把签到数量少于n个目标位置删除
place_count = data.groupby('place_id').count() # 以place_id为特征进行分组,统计次数
tf = place_count[place_count.row_id > 3].reset_index() # 保留签到次数大于3的目标值
data = data[data['place_id'].isin(tf.place_id)] # 保留与tf相同的place_id
data = data.drop(['row_id'],axis=1) # 删除签到次数,与结果无关
print(data)
# 取出数据中的特征值和目标值
y = data['place_id']
x = data.drop(['place_id'],axis=1)
# 进行数据的分割,训练集和测试集
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25)
# 特征工程(标准化)
std = StandardScaler()
# 对测试集和训练集的特征值进行标准化
x_train = std.fit_transform(x_train)
x_test = std.transform(x_test)
# 进行算法流程
knn = KNeighborsClassifier(n_neighbors=5)
# fit,predict,score
knn.fit(x_train,y_train)
# 得出预测结果
y_predict = knn.predict(x_test)
print('预测的目标签到位置为:',y_predict)
# 得出预测的准确率
score = knn.score(x_test,y_test)
print('预测的准确率为:',score)
return None
if __name__ == '__main__':
knn_fen()预测的准确率为: 0.4787234042553192k近邻算法相关问题
k值取多大?有什么影响?
k值取很小:容易受异常点影响
k值取很大:容易受数据波动影响
优缺点
优点:
简单,易于理解,易于实现,无需估计参数,无需训练
缺点:
懒惰算法,对测试样本分类时的计算量大,内存开销大
必须指定K值,K值选择不当则分类精度不能保证
应用场景
小数据场景,几千~几万样本,具体场景具体业务去测试
案例——鸢尾花分类
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
def k_iris():
lr = load_iris()
x = lr.data
y = lr.target
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25)
std = StandardScaler()
x_train = std.fit_transform(x_train)
x_test = std.transform(x_test)
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(x_train,y_train)
y_predict = knn.predict(x_test)
print('预测的目标种类为:', y_predict)
score = knn.score(x_test,y_test)
print('预测的准确率:',score)
if __name__ == '__main__':
k_iris()预测的目标种类为: [0 2 1 2 0 2 2 2 0 2 0 2 1 0 2 0 0 1 2 2 1 1 2 2 1 2 1 1 1 0 1 0 1 1 2 2 2
1]
预测的准确率: 0.9736842105263158朴素贝叶斯算法
概率基础
概率定义为一件事情发生的可能性
联合概率和条件概率
联合概率:包含多个条件,且所有条件同时成立的概率——记作:P(A,B)
条件概率:就是事件A在另外一个事件B已经发生条件下的发生概率——记作:P(A|B)
特性:P(A1,A2|B) = P(A1|B)P(A2|B)
注意:此条件概率的成立,是由于A1,A2相互独立的结果
朴素贝叶斯——贝叶斯公式
P(文档类别|文档特征值)——注:w为给定文档的特征值(频数统计,预测文档提供),c为文档类别
其中C可以是不同类别
P(C):每个文档类别的概率(某文档类别词数/总文档词数)
P(W│C):给定类别下特征(被预测文档中出现的词)的概率
计算方法:P(F1│C)=Ni/N (训练文档中去计算)
Ni为该F1词在C类别所有文档中出现的次数
N为所属类别C下的文档所有词出现的次数和
P(F1,F2,…)预测文档中每个词的概率
拉普拉斯平滑系数
问题:从上面的例子我们得到娱乐概率为0,这是不合理的,如果词频列表里面有很多出现次数都为0,很可能计算结果都为零
解决方法:拉普拉斯平滑系数
P(F1│C)=(Ni+α)/(N+αm)
α为指定的系数一般为1,m为训练文档中统计出的特征词个数
sklearn朴素贝叶斯实现API
sklearn.naive_bayes.MultinomialNB(alpha=1.0)——朴素贝叶斯分类
alpha:拉普拉斯平滑系数(对结果没影响)
案例——20类新闻文本分类
1、加载20类新闻数据,并进行分割
2、生成文章特征词
3、朴素贝叶斯estimator流程进行预估
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
def naviebayes():
"""
朴素贝叶斯进行文本分类
:return:
"""
news = fetch_20newsgroups(subset='all')
# 进行数据分割
x_train,x_test,y_train,y_test = train_test_split(news.data,news.target,test_size=0.25)
# 对文本进行特征抽取
tf = TfidfVectorizer()
# 以训练集当中的词的列表进行每篇文章重要性统计
x_train = tf.fit_transform(x_train)
print(tf.get_feature_names())
x_test = tf.transform(x_test)
# 进行朴素贝叶斯算法的预测
mlt = MultinomialNB(alpha=1.0)
print(x_train.toarray())
mlt.fit(x_train,y_train)
y_predict = mlt.predict(x_test)
print('预测的文章类别:',y_predict)
# 得出准确率
score = mlt.score(x_test,y_test)
print('预测的准确率为:',score)
return None
if __name__=='__main__':
naviebayes()预测的文章类别: [12 10 15 ... 15 7 10]
预测的准确率为: 0.8491086587436333朴素贝叶斯分类的优缺点
优点:
1、朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
2、对缺失数据不太敏感,算法也比较简单,常用于文本分类。
3、分类准确度高,速度快
缺点:
1、需要知道先验概率P(F1,F2,…|C),因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
2、朴素贝叶斯算法假设了文章当中一些与另外一些词是独立没关系的——不太靠谱
3、朴素贝叶斯是在训练集当中进行统计词这些工作——会对结果造成干扰
注:
1、训练集误差大,效果肯定不好
2、不需要调参
分类模型的评估
estimator.score()——一般最常见使用的是准确率,即预测结果正确的百分比
但有些场景下,不仅要考虑准确率还要考虑精确率和召回率以及F1-score
- 准确率:患癌、不患癌多少预测对了
- 精确率:预测患癌的里面多少真患癌了
- 召回率:患癌的,都被预测到了吗
- F1-score:综合评估标准
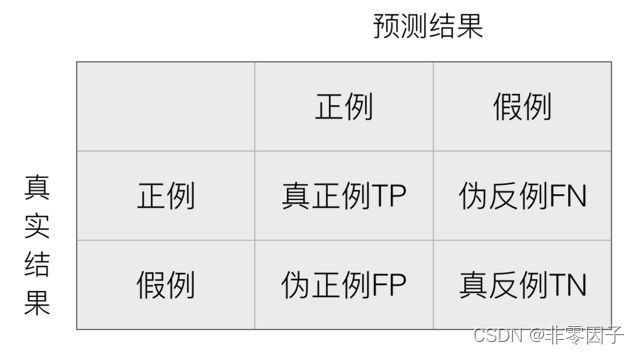
混淆矩阵
在分类任务下,预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合,构成混淆矩阵(适用于多分类)
精确率(Precision)与召回率(Recall)以及F1-score
精确率:预测结果为正例样本中真实为正例的比例(查得准)
召回率:真实为正例的样本中预测结果为正例的比例(查的全,对正样本的区分能力)——要查的样本是不是都查到了
其他分类标准,F1-score,反映了模型的稳健型——综合评判标准
分类模型评估API
sklearn.metrics.classification_report(y_true, y_pred, target_names=None)
- y_true:真实目标值
- y_pred:估计器预测目标值
- target_names:目标类别名称
- return:每个类别精确率与召回率
from sklearn.metrics import classification_report
PRF = classification_report(y_test,y_predict,target_names = news.target_names)
print('每个类别的精确率和召回率为:',PRF)应用场景:检测癌症病人,把失败产品检测出来等
模型的选择与调优
交叉验证——n折
为了让被评估的模型更加准确可信
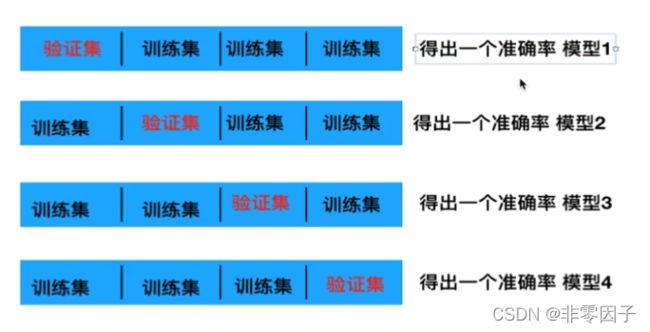
交叉验证:将拿到的数据,分为训练和验证集。以下图为例:将数据分成5份,其中一份作为验证集。然后经过5次(组)的测试,每次都更换不同的验证集。即得到5组模型的结果,取平均值作为最终结果。又称5折交叉验证
1、所有数据分为n等分
2、4个准确率求平均值——称为4折交叉验证
网格搜索——调参数
K近邻——超参数k
通常情况下,有很多参数是需要手动指定的(如k-近邻算法中的K值),这种叫超参数。但是手动过程繁杂,所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。
超参数搜索-网格搜索API
sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)——对估计器的指定参数值进行详尽搜索
- estimator:估计器对象
- param_grid:估计器参数(dict){“n_neighbors”:[1,3,5]}
- cv:指定几折交叉验证
- fit:输入训练数据
- score:准确率
结果分析:
- best_score_:在交叉验证中测试的最好结果
- best_estimator_:最好的参数模型
- cv_results_:每次交叉验证后的测试集准确率结果和训练集准确率结果
from sklearn.model_selection import GridSearchCV
param = {"n_neighbors":[3,5,10]}
# 进行网格搜索
gc = GridSearchCV(knn,param_grid=param,cv=2)
gc.fit(x_train,y_train)
# 预测准确率
score = gc.score(x_test,y_test)
print('在测试集上的准确率:',score)
print('在交叉验证中最好的结果:',gc.best_score_)
print('选择最好的模型是:',gc.best_estimator_)
print('每个超参数每次交叉验证后的结果为:',gc.cv_results_)在测试集上的准确率: 0.484160756501182
在交叉验证中最好的结果: 0.44404161412358134
选择最好的模型是: KNeighborsClassifier(n_neighbors=10)
[{'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 10}], 'split0_test_score': array([0.42449559, 0.44025851, 0.44293821]), 'split1_test_score': array([0.42591425, 0.43883985, 0.44514502]), 'mean_test_score': array([0.42520492, 0.43954918, 0.44404161])]