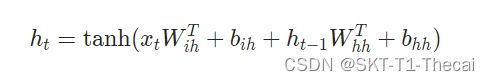Pytorch中的RNN

Pytorch中的RNN

本文希望通过对RNN中的参数分析，进一步熟悉RNN的结构和原理。

原始程序

首先构建一个简单的RNN，一层，输入向量长度为3，隐藏变量长度为2，
并随机生成初始参数h0，先后打印h0，output，hn以及rnn中的所有参数

import torch
import torch.nn as nn
A = torch.tensor([
    [1,2,3],[2,3,4],[3,4,5]
],dtype=torch.float).unsqueeze(0)

rnn = nn.RNN(input_size=3,hidden_size=2,num_layers=1)
h0 = torch.rand((1,3,2),dtype=torch.float)
print("h0",h0)
output,hn = rnn(A,h0)
print(output)
print(hn)
for k,v in rnn.named_parameters():
    print("k:",k)
    print("v:",v)
    print("-"*50)

程序的输出如下：
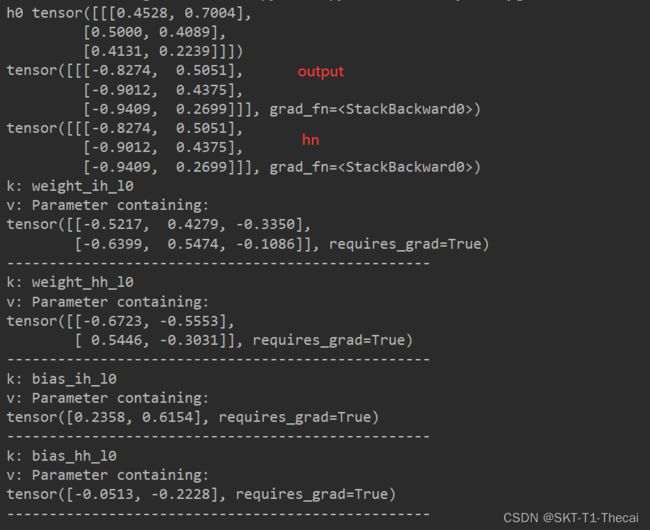可以发现output和hn是相同的，是因为output就是取RNN最后一层的隐藏状态，这个网络只有一层，所以两者是相同的。此外每一层有两个矩阵Whh和Wih以及两个偏置Bhh和Bih

参数分析

把刚才的输出在一个新的程序中记录下来，用于验证RNN的计算过程。

import torch
x1 = torch.asarray([1.0,2.0,3.0])
x2 = torch.asarray([2.0,3.0,4.0])
x3 = torch.asarray([3.0,4.0,5.0])
h0 = torch.asarray([0.4528,0.7004])
h1 = torch.asarray([0.5000,0.4089])
h2 = torch.asarray([0.4131,0.2239])
wih = torch.asarray([[-0.5217,  0.4279, -0.3350],
        [-0.6399,  0.5474, -0.1086]])
whh = torch.asarray([[-0.6723, -0.5553],
        [ 0.5446, -0.3031]]
)
bih = torch.asarray([0.2358, 0.6154])
bhh = torch.asarray([-0.0513, -0.2228])

print("h0",torch.tanh(torch.matmul(x1.unsqueeze(0),wih.transpose(0,1))+bih.unsqueeze(0)
      +torch.matmul(h0.unsqueeze(0),whh.transpose(0,1))+bhh.unsqueeze(0)))
print("h1",torch.tanh(torch.matmul(x2.unsqueeze(0),wih.transpose(0,1))+bih.unsqueeze(0)
      +torch.matmul(h1.unsqueeze(0),whh.transpose(0,1))+bhh.unsqueeze(0)))
print("h2",torch.tanh(torch.matmul(x3.unsqueeze(0),wih.transpose(0,1))+bih.unsqueeze(0)
      +torch.matmul(h2.unsqueeze(0),whh.transpose(0,1))+bhh.unsqueeze(0)))

其中的计算过程来自Pytorch官方文档

打印结果如下：

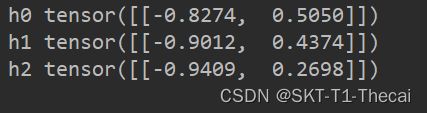
可以发现和之前RNN输出的隐藏状态是一样的：

但是这里有一个问题，以上的代码没有体现时序，如果更改x1，那么只有第一个隐藏变量会变化，其他两个不会变化，换句话说，上述打印隐藏状态的ht-1并不是真正的前一时刻的隐藏状态，而是输入值，待解决。