PaddlePaddle飞桨练习——使用Python和NumPy构建神经网络模型(以波士顿房价为例)
一、首先我们根据飞桨paddlepaddle中的安装教程进行环境配置。
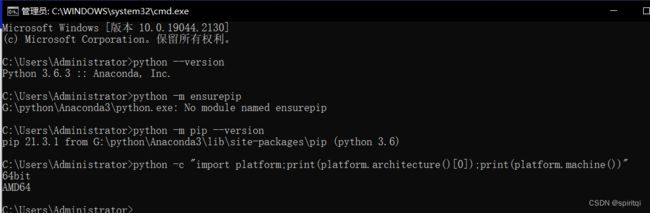
1.需要确认python的版本是否满足要求(我这里使用的为python3.6)
2.需要确认pip的版本是否满足要求,要求pip版本为20.2.2或更高版本(我这里使用的为21.3.1版本,符合要求)
3.需要确认Python和pip是64bit,并且处理器架构是x86_64(或称作x64、Intel 64、AMD64)架构。下面的第一行输出的是”64bit”,第二行输出”x86_64”、”x64”或”AMD64”即可(如上图所示)
检视完毕后我们按照步骤进行安装,安装完毕后我们进行验证:
其中我们经历了一些安装问题:
在这里我们pip版本为低版本不符合要求,所以我们需要更新pip版本
命令为:python -m pip install --upgrade pip
显示 PaddlePaddle is installed successfully! 说明我们已成功安装。
二、我们进行实例练习:
可以使用在线平台也可以使用自己的pycharm等编程软件。
这里我们使用PaddlePaddle网站中的在线环境平台进行编程训练。
1.读入数据:通过飞桨论坛获取波士顿房价数据并导入。
具体代码如下:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def load_data():
# 从文件导入数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原始数据进行Reshape,变成[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# 计算训练集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
#np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
N = x.shape[0]
gradient_w = 1. / N * np.sum((z-y) * x, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = 1. / N * np.sum(z-y)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta = 0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, training_data, num_epochs, batch_size=10, eta=0.01):
n = len(training_data)
losses = []
for epoch_id in range(num_epochs):
# 在每轮迭代开始之前,将训练数据的顺序随机打乱
# 然后再按每次取batch_size条数据的方式取出
np.random.shuffle(training_data)
# 将训练数据进行拆分,每个mini_batch包含batch_size条的数据
mini_batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]
for iter_id, mini_batch in enumerate(mini_batches):
#print(self.w.shape)
#print(self.b)
x = mini_batch[:, :-1]
y = mini_batch[:, -1:]
a = self.forward(x)
loss = self.loss(a, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(loss)
print('Epoch {:3d} / iter {:3d}, loss = {:.4f}'.
format(epoch_id, iter_id, loss))
return losses
# 获取数据
train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
# 创建网络
net = Network(13)
# 启动训练
losses = net.train(train_data, num_epochs=50, batch_size=100, eta=0.1)
# 画出损失函数的变化趋势
plot_x = np.arange(len(losses))
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()基本分析:
1.使用numpy loadtxt函数导入数据集的housing2.data文件并进行数据归一化处理
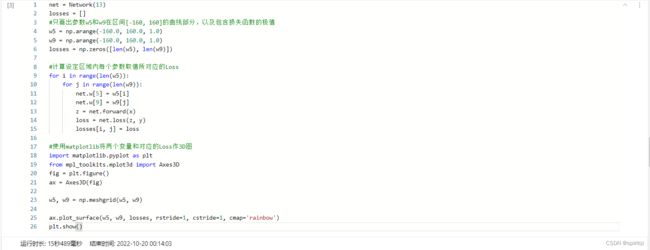
2.使用线性回归模型(随机产生w的初始值)
梯度下降方向示意图
3.梯度计算(使用梯度下降法)运行出来结果为:
Epoch 0 / iter 0, loss = 6.0789 Epoch 0 / iter 1, loss = 2.5661 Epoch 0 / iter 2, loss = 1.1954 Epoch 0 / iter 3, loss = 1.1720 Epoch 0 / iter 4, loss = 0.6296 Epoch 1 / iter 0, loss = 0.4763 Epoch 1 / iter 1, loss = 0.4433 Epoch 1 / iter 2, loss = 0.6048 Epoch 1 / iter 3, loss = 0.6297 Epoch 1 / iter 4, loss = 0.3486 Epoch 2 / iter 0, loss = 0.6003 Epoch 2 / iter 1, loss = 0.4231 Epoch 2 / iter 2, loss = 0.4524 Epoch 2 / iter 3, loss = 0.4943 Epoch 2 / iter 4, loss = 0.1017 Epoch 3 / iter 0, loss = 0.4592 Epoch 3 / iter 1, loss = 0.4666 Epoch 3 / iter 2, loss = 0.4256 Epoch 3 / iter 3, loss = 0.4656 Epoch 3 / iter 4, loss = 0.4929 Epoch 4 / iter 0, loss = 0.4383 Epoch 4 / iter 1, loss = 0.5079 Epoch 4 / iter 2, loss = 0.3804 Epoch 4 / iter 3, loss = 0.4277 Epoch 4 / iter 4, loss = 0.4963 Epoch 5 / iter 0, loss = 0.4781 Epoch 5 / iter 1, loss = 0.4061 Epoch 5 / iter 2, loss = 0.3995 Epoch 5 / iter 3, loss = 0.3223 Epoch 5 / iter 4, loss = 0.7517 Epoch 6 / iter 0, loss = 0.4506 Epoch 6 / iter 1, loss = 0.3313 Epoch 6 / iter 2, loss = 0.3938 Epoch 6 / iter 3, loss = 0.3739 Epoch 6 / iter 4, loss = 0.7127 Epoch 7 / iter 0, loss = 0.3191 Epoch 7 / iter 1, loss = 0.3361 Epoch 7 / iter 2, loss = 0.3282 Epoch 7 / iter 3, loss = 0.4023 Epoch 7 / iter 4, loss = 0.2349 Epoch 8 / iter 0, loss = 0.2980 Epoch 8 / iter 1, loss = 0.3217 Epoch 8 / iter 2, loss = 0.3729 Epoch 8 / iter 3, loss = 0.3147 Epoch 8 / iter 4, loss = 0.1023 Epoch 9 / iter 0, loss = 0.3250 Epoch 9 / iter 1, loss = 0.3472 Epoch 9 / iter 2, loss = 0.3463 Epoch 9 / iter 3, loss = 0.2266 Epoch 9 / iter 4, loss = 0.3066 Epoch 10 / iter 0, loss = 0.3789 Epoch 10 / iter 1, loss = 0.2772 Epoch 10 / iter 2, loss = 0.3135 Epoch 10 / iter 3, loss = 0.2112 Epoch 10 / iter 4, loss = 0.1040 Epoch 11 / iter 0, loss = 0.3367 Epoch 11 / iter 1, loss = 0.2811 Epoch 11 / iter 2, loss = 0.2401 Epoch 11 / iter 3, loss = 0.2533 Epoch 11 / iter 4, loss = 0.3783 Epoch 12 / iter 0, loss = 0.2174 Epoch 12 / iter 1, loss = 0.3007 Epoch 12 / iter 2, loss = 0.2921 Epoch 12 / iter 3, loss = 0.2894 Epoch 12 / iter 4, loss = 0.2546 Epoch 13 / iter 0, loss = 0.2458 Epoch 13 / iter 1, loss = 0.2193 Epoch 13 / iter 2, loss = 0.3270 Epoch 13 / iter 3, loss = 0.2239 Epoch 13 / iter 4, loss = 0.1167 Epoch 14 / iter 0, loss = 0.2471 Epoch 14 / iter 1, loss = 0.2495 Epoch 14 / iter 2, loss = 0.2165 Epoch 14 / iter 3, loss = 0.2702 Epoch 14 / iter 4, loss = 0.3491 Epoch 15 / iter 0, loss = 0.2270 Epoch 15 / iter 1, loss = 0.2257 Epoch 15 / iter 2, loss = 0.2339 Epoch 15 / iter 3, loss = 0.2589 Epoch 15 / iter 4, loss = 0.0954 Epoch 16 / iter 0, loss = 0.2318 Epoch 16 / iter 1, loss = 0.2437 Epoch 16 / iter 2, loss = 0.1966 Epoch 16 / iter 3, loss = 0.2055 Epoch 16 / iter 4, loss = 0.2777 Epoch 17 / iter 0, loss = 0.1998 Epoch 17 / iter 1, loss = 0.1929 Epoch 17 / iter 2, loss = 0.1878 Epoch 17 / iter 3, loss = 0.2638 Epoch 17 / iter 4, loss = 0.0628 Epoch 18 / iter 0, loss = 0.1965 Epoch 18 / iter 1, loss = 0.2294 Epoch 18 / iter 2, loss = 0.2032 Epoch 18 / iter 3, loss = 0.1912 Epoch 18 / iter 4, loss = 0.0968 Epoch 19 / iter 0, loss = 0.1806 Epoch 19 / iter 1, loss = 0.2139 Epoch 19 / iter 2, loss = 0.1874 Epoch 19 / iter 3, loss = 0.1980 Epoch 19 / iter 4, loss = 0.0729 Epoch 20 / iter 0, loss = 0.1919 Epoch 20 / iter 1, loss = 0.1855 Epoch 20 / iter 2, loss = 0.2116 Epoch 20 / iter 3, loss = 0.1557 Epoch 20 / iter 4, loss = 0.3469 Epoch 21 / iter 0, loss = 0.1767 Epoch 21 / iter 1, loss = 0.1816 Epoch 21 / iter 2, loss = 0.1584 Epoch 21 / iter 3, loss = 0.1998 Epoch 21 / iter 4, loss = 0.2794 Epoch 22 / iter 0, loss = 0.1418 Epoch 22 / iter 1, loss = 0.1936 Epoch 22 / iter 2, loss = 0.2080 Epoch 22 / iter 3, loss = 0.1527 Epoch 22 / iter 4, loss = 0.0835 Epoch 23 / iter 0, loss = 0.1929 Epoch 23 / iter 1, loss = 0.1483 Epoch 23 / iter 2, loss = 0.1689 Epoch 23 / iter 3, loss = 0.1591 Epoch 23 / iter 4, loss = 0.3369 Epoch 24 / iter 0, loss = 0.1543 Epoch 24 / iter 1, loss = 0.1454 Epoch 24 / iter 2, loss = 0.2189 Epoch 24 / iter 3, loss = 0.1288 Epoch 24 / iter 4, loss = 0.1101 Epoch 25 / iter 0, loss = 0.1570 Epoch 25 / iter 1, loss = 0.1901 Epoch 25 / iter 2, loss = 0.1225 Epoch 25 / iter 3, loss = 0.1693 Epoch 25 / iter 4, loss = 0.0467 Epoch 26 / iter 0, loss = 0.1524 Epoch 26 / iter 1, loss = 0.1716 Epoch 26 / iter 2, loss = 0.1475 Epoch 26 / iter 3, loss = 0.1327 Epoch 26 / iter 4, loss = 0.0409 Epoch 27 / iter 0, loss = 0.1409 Epoch 27 / iter 1, loss = 0.1477 Epoch 27 / iter 2, loss = 0.1478 Epoch 27 / iter 3, loss = 0.1481 Epoch 27 / iter 4, loss = 0.1916 Epoch 28 / iter 0, loss = 0.1425 Epoch 28 / iter 1, loss = 0.1485 Epoch 28 / iter 2, loss = 0.1403 Epoch 28 / iter 3, loss = 0.1366 Epoch 28 / iter 4, loss = 0.2062 Epoch 29 / iter 0, loss = 0.1162 Epoch 29 / iter 1, loss = 0.1140 Epoch 29 / iter 2, loss = 0.1565 Epoch 29 / iter 3, loss = 0.1611 Epoch 29 / iter 4, loss = 0.1048 Epoch 30 / iter 0, loss = 0.1342 Epoch 30 / iter 1, loss = 0.1495 Epoch 30 / iter 2, loss = 0.1337 Epoch 30 / iter 3, loss = 0.1154 Epoch 30 / iter 4, loss = 0.0992 Epoch 31 / iter 0, loss = 0.1442 Epoch 31 / iter 1, loss = 0.1428 Epoch 31 / iter 2, loss = 0.1144 Epoch 31 / iter 3, loss = 0.1183 Epoch 31 / iter 4, loss = 0.0459 Epoch 32 / iter 0, loss = 0.1208 Epoch 32 / iter 1, loss = 0.1477 Epoch 32 / iter 2, loss = 0.1107 Epoch 32 / iter 3, loss = 0.1361 Epoch 32 / iter 4, loss = 0.1011 Epoch 33 / iter 0, loss = 0.1379 Epoch 33 / iter 1, loss = 0.1082 Epoch 33 / iter 2, loss = 0.1211 Epoch 33 / iter 3, loss = 0.1208 Epoch 33 / iter 4, loss = 0.1429 Epoch 34 / iter 0, loss = 0.1477 Epoch 34 / iter 1, loss = 0.1159 Epoch 34 / iter 2, loss = 0.1021 Epoch 34 / iter 3, loss = 0.1141 Epoch 34 / iter 4, loss = 0.1373 Epoch 35 / iter 0, loss = 0.1154 Epoch 35 / iter 1, loss = 0.1169 Epoch 35 / iter 2, loss = 0.1359 Epoch 35 / iter 3, loss = 0.1085 Epoch 35 / iter 4, loss = 0.0618 Epoch 36 / iter 0, loss = 0.0959 Epoch 36 / iter 1, loss = 0.0930 Epoch 36 / iter 2, loss = 0.1592 Epoch 36 / iter 3, loss = 0.1029 Epoch 36 / iter 4, loss = 0.1095 Epoch 37 / iter 0, loss = 0.1150 Epoch 37 / iter 1, loss = 0.1085 Epoch 37 / iter 2, loss = 0.0992 Epoch 37 / iter 3, loss = 0.1203 Epoch 37 / iter 4, loss = 0.1618 Epoch 38 / iter 0, loss = 0.0713 Epoch 38 / iter 1, loss = 0.1188 Epoch 38 / iter 2, loss = 0.1511 Epoch 38 / iter 3, loss = 0.0889 Epoch 38 / iter 4, loss = 0.2266 Epoch 39 / iter 0, loss = 0.0872 Epoch 39 / iter 1, loss = 0.1136 Epoch 39 / iter 2, loss = 0.1233 Epoch 39 / iter 3, loss = 0.1001 Epoch 39 / iter 4, loss = 0.0648 Epoch 40 / iter 0, loss = 0.1059 Epoch 40 / iter 1, loss = 0.1394 Epoch 40 / iter 2, loss = 0.0855 Epoch 40 / iter 3, loss = 0.0827 Epoch 40 / iter 4, loss = 0.0279 Epoch 41 / iter 0, loss = 0.1222 Epoch 41 / iter 1, loss = 0.0880 Epoch 41 / iter 2, loss = 0.0875 Epoch 41 / iter 3, loss = 0.1035 Epoch 41 / iter 4, loss = 0.1090 Epoch 42 / iter 0, loss = 0.1014 Epoch 42 / iter 1, loss = 0.1009 Epoch 42 / iter 2, loss = 0.0967 Epoch 42 / iter 3, loss = 0.0951 Epoch 42 / iter 4, loss = 0.0444 Epoch 43 / iter 0, loss = 0.1110 Epoch 43 / iter 1, loss = 0.0898 Epoch 43 / iter 2, loss = 0.0876 Epoch 43 / iter 3, loss = 0.0964 Epoch 43 / iter 4, loss = 0.2259 Epoch 44 / iter 0, loss = 0.0801 Epoch 44 / iter 1, loss = 0.1053 Epoch 44 / iter 2, loss = 0.0885 Epoch 44 / iter 3, loss = 0.1184 Epoch 44 / iter 4, loss = 0.0270 Epoch 45 / iter 0, loss = 0.0999 Epoch 45 / iter 1, loss = 0.0734 Epoch 45 / iter 2, loss = 0.1011 Epoch 45 / iter 3, loss = 0.0957 Epoch 45 / iter 4, loss = 0.0427 Epoch 46 / iter 0, loss = 0.0930 Epoch 46 / iter 1, loss = 0.0886 Epoch 46 / iter 2, loss = 0.0935 Epoch 46 / iter 3, loss = 0.0888 Epoch 46 / iter 4, loss = 0.0105 Epoch 47 / iter 0, loss = 0.0950 Epoch 47 / iter 1, loss = 0.0981 Epoch 47 / iter 2, loss = 0.0951 Epoch 47 / iter 3, loss = 0.0686 Epoch 47 / iter 4, loss = 0.0171 Epoch 48 / iter 0, loss = 0.1082 Epoch 48 / iter 1, loss = 0.0752 Epoch 48 / iter 2, loss = 0.0754 Epoch 48 / iter 3, loss = 0.0838 Epoch 48 / iter 4, loss = 0.2349 Epoch 49 / iter 0, loss = 0.0956 Epoch 49 / iter 1, loss = 0.0893 Epoch 49 / iter 2, loss = 0.0724 Epoch 49 / iter 3, loss = 0.0885 Epoch 49 / iter 4, loss = 0.0744