ccc-sklearn-4-特征降维

1.维度的概念

对于数组和Series，维度就是shape返回的数字个数。其中一行和一列都称为1维

对于一个特征矩阵或者DateFrame，维度指样本的数量或者特征的数量，一般都是特征的数量

对于图像来说，维度就是图像中特征向量的数量。各个特征向量之间相互垂直

降维算法的目的

• 降低特征矩阵中特征的数量，让算法运算更快，效果更好
• 对于三维以上的矩阵无法可视化，降维可以帮助可视化的实现，利于对于数据的直观理解

2.sklearn中的降维算法

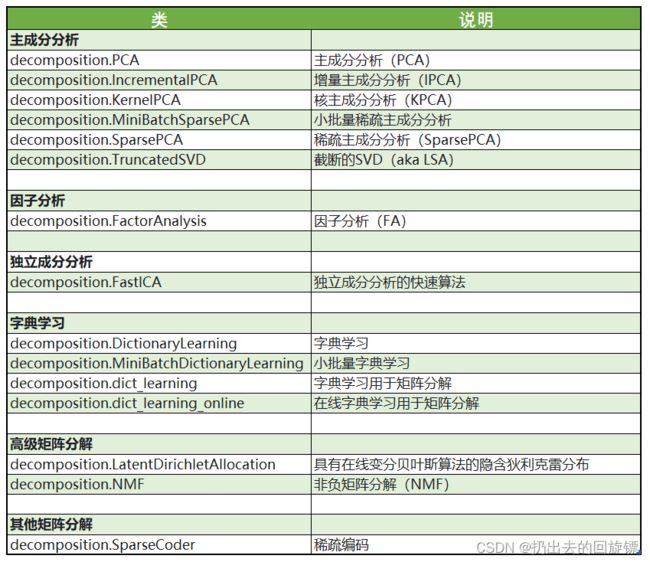
sklearn的降维算法都在模块decomposition中，本质是一个矩阵分解模块。在降维、深度学习、聚类分析、数据预处理、低纬度特征、大数据分析等领域都广泛使用

PCA与SVD

在降维的过程中，希望减少特征数量的同时保留大部分有效信息，删除带无效的信息的特征的新的特征矩阵

PCA使用信息量衡量指标是样本方差，即可解释性方差，越大说明特征携带的信息量越多
$$Var=\frac{1}{n-1}\sum _{i=1}^n(x_i-\hat{x}{)}^2$$
Var代表一个特征的方差，n代表样本量，$x_i$表示一个特征中的每个样本取值，$\hat{x}$表示样本均值

说明：计算样本方差时为什么是除以（n-1）？

原则就是得到样本方差的无偏估计。所谓“无偏”，就是说，样本值应该是围绕总体值上下波动的，它不能总在总体值的上面，或者总在总体值下面。数学上可以证明：


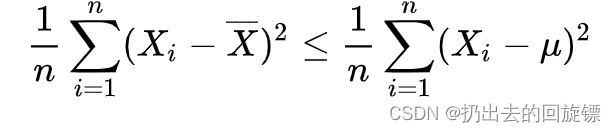
这样总是小于就不是无偏估计了，所以需要进行修正。至于修正的过程这里暂时不做解释。

降维是如何实现的
一组简单的二维数据降维

从二维到n维降维的基本过程：

过程	二维特征矩阵	n维特征矩阵
1	输入原数据，结构（3,2） 找出原本2个特征对应的直角坐标系	输入原数据，结构（m,n） 找出原本n个特征构成的n维空间V
2	决定降维后的特征数量：1	决定降维后的特征数量：k
3	旋转，找出新的坐标系，将新特征向量被压缩并不损失太多总信息量	通过某种变化，找出n个新的特征向量以及这些向量构成的n维空间V
4	找出数据在新的坐标系上，2个坐标轴上的坐标	找出原数据在新特征空间V中的n个新特征对应的值
5	选第一个方差最大的特征向量，删掉没有被选中的特征	选前k个信息量最大的特征，删除没有被选中的特征

说明：

• 不通降维算法都遵循这上面的步骤来进行降维，不同的是它们的第三部矩阵分解的算法不同，信息量的衡量指标也不同
• 特征选择是选择已有特征携带有信息最多的特征，选择后特征依然可以找到其在原数据的位置，代表的含义；PCA这种属于特征创造，即新特征举证生成前，无法知晓PCA建立了怎样的新特征向量，新特征向量生成后也不具有可读性，虽然带有原始数据的信息，但已经不是原始数据携带的含义了，所以PAC一般不适用于探索特征和标签之间的关系的模型

重要参数n_components与实际可视化案例
n_components即降维后需要保留的特征数量

步骤一：调库和数据

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA

iris = load_iris()
y = iris.target
X = iris.data
X.shape

步骤二：实例化建模

pca = PCA(n_components=2)
pca = pca.fit(X)
x_dr = pca.transform(X)
x_dr

步骤三：可视化绘图

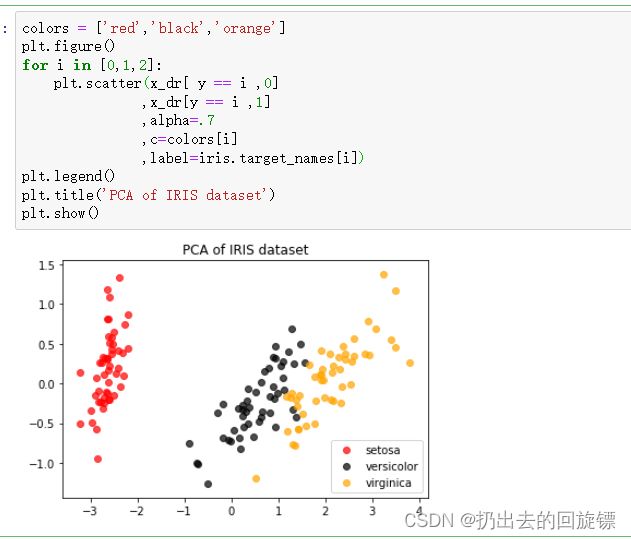
colors = ['red','black','orange']
plt.figure()
for i in [0,1,2]:
    plt.scatter(x_dr[ y == i ,0]
               ,x_dr[y == i ,1]
               ,alpha=.7
               ,c=colors[i]
               ,label=iris.target_names[i])
plt.legend()
plt.title('PCA of IRIS dataset')
plt.show()

步骤四：探索降维后的数据

#查看降维后每个特征携带的信息量的大小
pca.explained_variance_
#查看降维后每个新特征所占信息量站原数据的百分比
pca.explained_variance_ratio_
pca.explained_variance_ratio_.sum()

步骤五：绘制累计可解释方差贡献率曲线

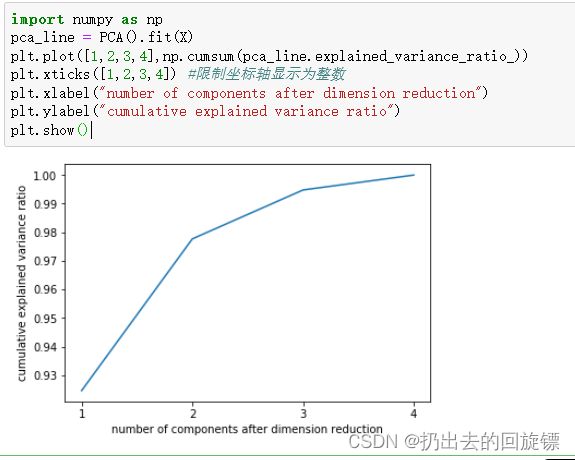
用于帮助我们决定n_components中最好的取值

import numpy as np
pca_line = PCA().fit(X)
plt.plot([1,2,3,4],np.cumsum(pca_line.explained_variance_ratio_))
plt.xticks([1,2,3,4]) #限制坐标轴显示为整数
plt.xlabel("number of components after dimension reduction")
plt.ylabel("cumulative explained variance ratio")
plt.show()

步骤六：使用mle自动选择特征

pca_mle = PCA(n_components="mle")
pca_mle = pca_mle.fit(X)
X_mle = pca_mle.transform(X)
X_mle

pca_mle.explained_variance_ratio_.sum()

可以看出它自动选择了3个参数

步骤七：按照信息占比选超参数

pca_f = PCA(n_components=0.95,svd_solver="full")
pac_f = pca_f.fit(X)
X_f = pca_f.transform(X)
pca_f.explained_variance_ratio_.sum()

PCA中的SVD是什么？
svd_solver：奇异值分解器，可以不结算协方差等结构复杂、计算冗长的矩阵，直接求出新特征空间和降维后的特征矩阵

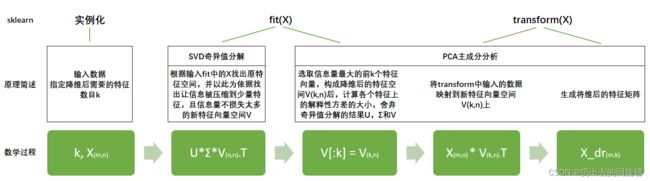
从流程中看到，sklearn中通过SVD求出特征空间，这样减少了计算量。可以认为fit中的矩阵U和Σ之后被舍弃，奇异值分解追求仅仅是V，保存在components_中

说明：右奇异矩阵$V^T$具有以下特征：

$$X_{dr}=X\ast V[:k{]}^T$$
k就是n_components，是我们降维后希望得到的维度。若X为(m,n)的特征矩阵， 就是结构为(n,n)的矩阵，取这个矩阵的前k行（进行切片），即将V转换为结构为(k,n)的矩阵。而$V_{(k,n)}^T$与原特征矩阵X相乘，即可得到降维后的特征矩阵X_dr

svd_solver可选参数：默认auto

• auto:基于X.shape和n_components的默认策略来选择分解器：如果输入数据的尺寸大于500x500且要提取的特征数小于数据最小维度min(X.shape)的80％，就启用效率更高的”randomized“方法。否则，精确完整的SVD将被计算，截断将会在矩阵被分解完成后有选择地发生
• full:从scipy.linalg.svd中调用标准的LAPACK分解器来生成精确完整的SVD，适合数据量比较适中，计算时间充足的情况，生成的精确完整的SVD的结构为：$$U_{(}m,m),\sum {}_{(m,n)},V_{(n,n)}^T$$
• arpack:从scipy.sparse.linalg.svds调用ARPACK分解器来运行截断奇异值分解(SVD truncated)，分解时就将特征数量降到n_components中输入的数值k，可以加快运算速度，适合特征矩阵很大的时候，但一般用于特征矩阵为稀疏矩阵的情况，包含一定的随机性。截断后的SVD分解出的结构为:$$U_{(}m,k),\sum {}_{(k,k)},V_{(n,n)}^T$$
• randomized:根据原始数据和输入的n_components值去计算和寻找符合需求的新特征向量，但是在"randomized"方法中，分解器会先生成多个随机向量，然后去检测这些随机向量中是否有任何一个符合我们的分解需求，如果符合，就保留这个随机向量，并基于这个随机向量来构建后续的向量空间。比"full"模式下计算快很多，并且还能够保证模型运行效果。适合特征矩阵巨大，计算量庞大的情况（svd_solver的值为"arpack" or "randomized"生效）

3.人脸识别案例与手写字识别噪音过滤

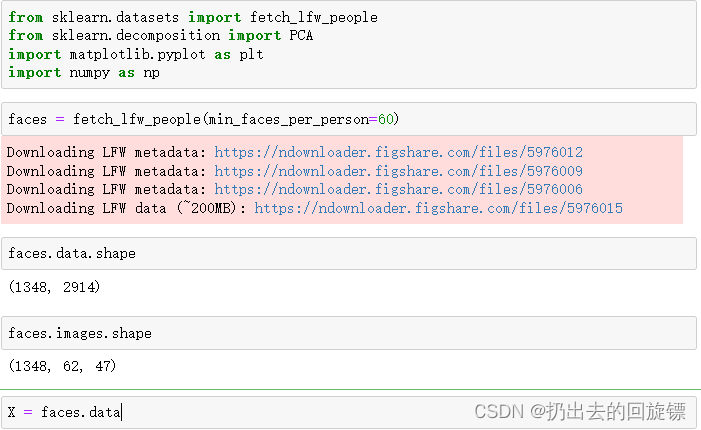
步骤一：导入库和数据

from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np
faces = fetch_lfw_people(min_faces_per_person=60)
X = faces.data

步骤二：原始特征可视化

fig, axes = plt.subplots(4,5
                       ,figsize=(8,4)
                       ,subplot_kw = {"xticks":[],"yticks":[]})
#subplot_kw控制坐标轴为空
#fig 画布
#axes 生成的子图对象

fig, axes = plt.subplots(3,8
                       ,figsize=(8,4)
                       ,subplot_kw = {"xticks":[],"yticks":[]})
for i, ax in enumerate(axes.flat):
    ax.imshow(faces.images[i,:,:],cmap="gray")

步骤三：原始数据降维，并将新生成新的可视化特征矩阵

pca = PCA(150).fit(X)
V = pca.components_
V.shape

fig, axes = plt.subplots(3,8
                       ,figsize=(8,4)
                       ,subplot_kw = {"xticks":[],"yticks":[]})
for i, ax in enumerate(axes.flat):
    ax.imshow(V[i,:].reshape(62,47),cmap="gray")

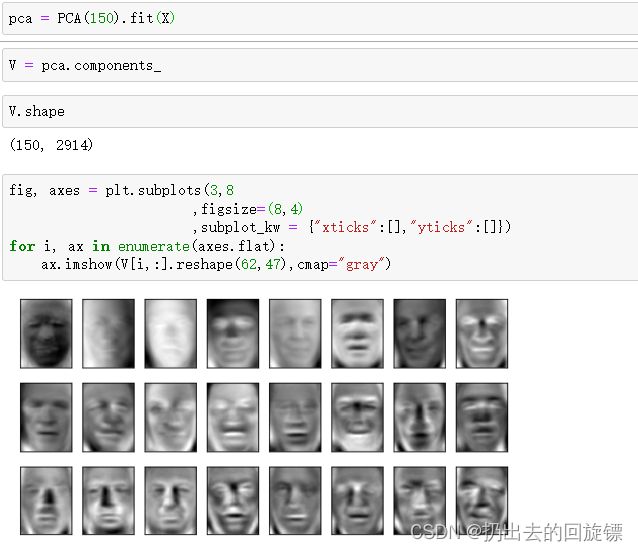
相对来说，眼睛，鼻子，嘴巴比较清晰，然而脸的轮廓和头发就变的模糊了。说明性特征的特征向量大多根据“五官”和“亮度”相关的特征中提取出来

步骤四：将降维后的矩阵还原图像查看信息保存量

x_dr = pca.fit_transform(X)
X_inverse = pca.inverse_transform(x_dr)

fig, ax = plt.subplots(2,10,figsize=(10,2.5)
                      ,subplot_kw={"xticks":[],"yticks":[]}
                      )
for i in range(10):
    ax[0,i].imshow(faces.images[i,:,:],cmap="binary_r")
    ax[1,i].imshow(X_inverse[i].reshape(62,47),cmap="binary_r")

虽然大部分相似，但是明显舍弃了部分信息。即降维不是完全可逆，但是也的确保留了原数据的大部分信息

PCA手写字噪音过滤：
步骤一：导入所需库和数据

from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np

digits = load_digits()

步骤二：定义画图函数

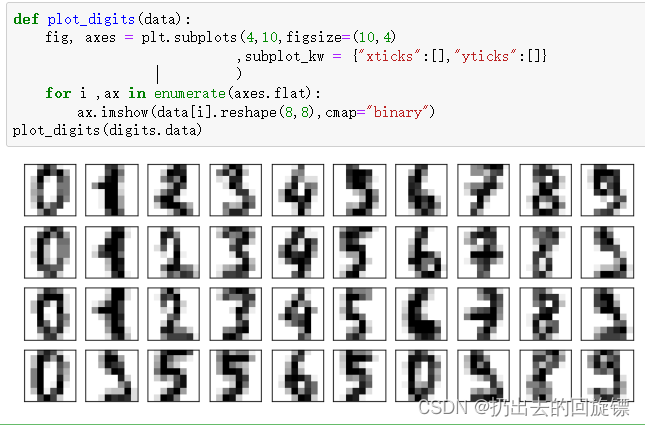
def plot_digits(data):
    fig, axes = plt.subplots(4,10,figsize=(10,4)
                            ,subplot_kw = {"xticks":[],"yticks":[]}
                            )
    for i ,ax in enumerate(axes.flat):
        ax.imshow(data[i].reshape(8,8),cmap="binary")
plot_digits(digits.data)

步骤三：加入噪音，并绘制

np.random.RandomState(42)
noisy = np.random.normal(digits.data,2)
plot_digits(noisy)

步骤四：PCA降维，并逆转还原绘图

pca = PCA(0.5).fit(noisy)
X_dr = pca.transform(noisy)
X_dr.shape

without_noise = pca.inverse_transform(X_dr)
plot_digits(without_noise)

可以看到，降噪实现比较完美

原理、流程、重要属性接口和参数总结

4.PCA实现784个特征的手写字降维

步骤一：导入库和数据

from sklearn.decomposition import PCA
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

data = pd.read_csv(r".\digit recognizor.csv")
 
X = data.iloc[:,1:]
y = data.iloc[:,0]

步骤二：绘制累计方差贡献曲线，找到最佳降维范围

pca_line = PCA().fit(X)
plt.figure(figsize=[20,5])
plt.plot(np.cumsum(pca_line.explained_variance_ratio_))
plt.xlabel("number of components after dimension reduction")
plt.ylabel("cumulative explained variance ratio")
plt.show()

步骤三：细化学习曲线

#======【TIME WARNING：2mins 30s】======#
 
score = []
for i in range(1,101,10):
    X_dr = PCA(i).fit_transform(X)
    once = cross_val_score(RFC(n_estimators=10,random_state=0)
                           ,X_dr,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(1,101,10),score)
plt.show()

score = []
for i in range(10,25):
    X_dr = PCA(i).fit_transform(X)
    once = cross_val_score(RFC(n_estimators=10,random_state=0),X_dr,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(10,25),score)
plt.show()

找到效果最好的22维结果

步骤四：验证22维的准确性，以及其他算法

X_dr = PCA(22).fit_transform(X)
 
#======【TIME WARNING:1mins 30s】======#
cross_val_score(RFC(n_estimators=100,random_state=0),X_dr,y,cv=5).mean()

from sklearn.neighbors import KNeighborsClassifier as KNN
cross_val_score(KNN(),X_dr,y,cv=5).mean()#KNN()的值不填写默认=5    

KNN的交叉验证

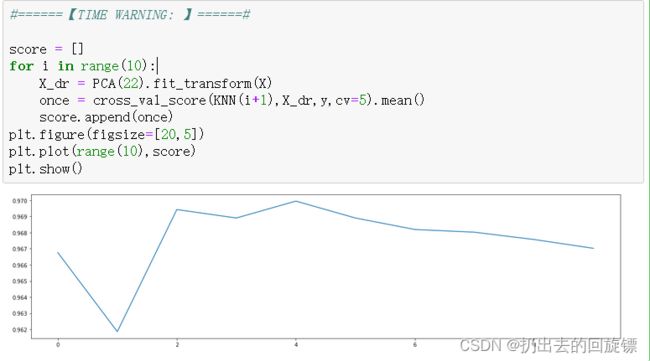
#======【TIME WARNING: 】======#

score = []
for i in range(10):
    X_dr = PCA(22).fit_transform(X)
    once = cross_val_score(KNN(i+1),X_dr,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(10),score)
plt.show()

KNN(4).fit(X_dr,y).score(X_dr,y)

附录：
1.PCA参数列表



2.PCA属性列表

3.PCA接口列表