（五）Softmax 回归

---

前言

这篇文章是关于 Softmax 回归算法的总结和代码实现，Softmax 回归算法可以借助广义线性模型推导，也可以和逻辑回归作对比，将其看成逻辑回归算法在多分类问题上的一个推广。

---

1. Softmax 回归模型

​如果有一个多分类问题需要我们处理，我们假设输出变量 $y$ 可能的取值为 $\left\{1,2,\cdots ,k\right\}$ ，特征向量还是 $x=\left(x_0,x_1,\cdots ,x_n\right)=\left(1,x_1,\cdots ,x_n\right)$ ，这时我们应该如何预测 $y$ 的取值呢？

​如果我们使用广义线性模型来设计一种分类模型，那么我们就可以按照广义线性模型的流程来推导多分类问题的模型，这也就是 softmax 回归模型。不过这个模型推导稍微繁琐，也就不推导了，先看看 Logistic 回归的情况，Logistic 回归使用这样的函数当做预测值为 $1$ 的概率：
$$P\left(y=1|x;\theta \right)=h_{\theta }\left(x\right)=\frac{1}{1+\exp \left(-{\theta }^{T}x\right)}$$
​这里的参数只使用了一个向量 $\theta$ ，如果我们使用两个参数 ${\theta }_0$ 和 ${\theta }_1$ ，使用下面的式子作为概率：
$$\begin{gathered} P\left(y=1|x;{\theta }_1,{\theta }_2\right)=\frac{\exp \left({\theta }_1^{T}x\right)}{\exp \left({\theta }_0^{T}x\right)+\exp \left({\theta }_1^{T}x\right)} \\ =\frac{1}{1+\exp \left[{\left({\theta }_0^T-{\theta }_1^T\right)}^{T}x\right]} \end{gathered}$$
如果 $\theta ={\theta }_1-{\theta }_0$ ，那么两种概率就一样了，这样做给了一种启发，对于多元分类问题，我们可以用下面的公式代表概率：
$$P\left(y=i|x;\theta \right)=\frac{\exp \left({\theta }_i^{T}x\right)}{{\sum }_{j=1}^k\exp \left({\theta }_j^{T}x\right)}\left(i=1,2,\cdots ,k\right)$$
其中 $\theta =\left({\theta }_1,{\theta }_2,\cdots ,{\theta }_k\right)$ ，${\theta }_i=\left({\theta }_{i0},{\theta }_{i1},{\theta }_{i2},\cdots ,{\theta }_{in}\right)$ ，可以这样来理解：**对每一个类别 $i$ ，都有一个参数 ${\theta }_i$ ， ${\theta }_i$ 是特征向量 $x$ 各个分量的权重，线性组合 ${\theta }_i^{T}x$ 越大，就说明特征向量 $x$ 越有可能属于类别 $i$ ，指数会放大每个线性组合 ${\theta }_i^{T}x$ 的差距，因此用指数作用，会使 $x$ 更确定地被分到某一类别中（这句话的意思是：如果原本特征向量属于类别 $i$ 的可能性最大，那么使用指数作用后，特征向量属于类别 $i$ 的可能会变得更加大，以一种更大的概率分类），而分母是为了归一化，使各项加和为 $1$ 。**由上述公式很容易得到这样的公式：
$$P\left(y^{\left(i\right)}|x^{\left(i\right)};\theta \right)=\frac{\exp \left({\theta }_{y^{\left(i\right)}}^T{x}^{\left(i\right)}\right)}{{\sum }_{j=1}^k\exp \left({\theta }_j^T{x}^{\left(i\right)}\right)}$$
接下来运用极大似然估计来求解参数。对数似然函数为：
$$l\left(\theta \right)=\sum _{i=1}^m\ln \frac{\exp \left({\theta }_{y^{\left(i\right)}}^T{x}^{\left(i\right)}\right)}{{\sum }_{j=1}^k\exp \left({\theta }_j^T{x}^{\left(i\right)}\right)}=\sum _{i=1}^m\left[{\theta }_{y^{\left(i\right)}}^T{x}^{\left(i\right)}-\ln \sum _{j=1}^k\exp \left({\theta }_j^T{x}^{\left(i\right)}\right)\right]$$
那么 $\theta =\underset{\theta }{\mathrm{argmax}}l\left(\theta \right)$ ，最大化这样的函数的过程就是参数训练的过程。

​Softmax 回归的损失函数可以定义为对数似然函数的负数，这和 Logistic 回归类似，损失函数为：
$$J\left(\theta \right)=-\sum _{i=1}^m\ln \frac{\exp \left({\theta }_{y^{\left(i\right)}}^T{x}^{\left(i\right)}\right)}{{\sum }_{j=1}^k\exp \left({\theta }_j^T{x}^{\left(i\right)}\right)}=\sum _{i=1}^m\left[\ln \sum _{j=1}^k\exp \left({\theta }_j^T{x}^{\left(i\right)}\right)-{\theta }_{y^{\left(i\right)}}^T{x}^{\left(i\right)}\right]$$

​Logistic 回归中有 $h_{\theta }\left(x\right)$ ，在 Softmax 回归中也有，它可以这样定义：
$$\begin{gathered} h_{\theta }\left(x\right)={\left[P\left(y=1|x;\theta \right),P\left(y=2|x;\theta \right),\cdots ,P\left(y=k|x;\theta \right)\right]}^T \\ ={\left[\frac{\exp \left({\theta }_1^{T}x\right)}{{\sum }_{j=1}^k\exp \left({\theta }_j^{T}x\right)},\frac{\exp \left({\theta }_2^{T}x\right)}{{\sum }_{j=1}^k\exp \left({\theta }_j^{T}x\right)},\cdots ,\frac{\exp \left({\theta }_k^{T}x\right)}{{\sum }_{j=1}^k\exp \left({\theta }_j^{T}x\right)}\right]}^T \end{gathered}$$

---

2. 优化方法

​要最小化损失函数梯度下降法是机器学习中很常用的方法，可以使用梯度下降法最小化损失函数，当然也可以使用别的优化方法来优化损失函数，例如牛顿迭代法。很多优化方法都是要求解函数的导数的，所以现在对损失函数求导，先看这几项导数：
$$\frac{\partial {\theta }_{y^{\left(i\right)}}^T{x}^{\left(i\right)}}{\partial {\theta }_l}=x^{\left(i\right)}I\left\{y^{\left(i\right)}=l\right\}$$
这里的 $I$ 是指示函数，$I\left\{true\right\}=1$ ，$I\left\{false\right\}=0$ 。
$$\frac{\partial \ln {\sum }_{j=1}^k\exp \left({\theta }_j^T{x}^{\left(i\right)}\right)}{\partial {\theta }_l}=\frac{\exp \left({\theta }_l^T{x}^{\left(i\right)}\right)x^{\left(i\right)}}{{\sum }_{j=1}^k\exp \left({\theta }_j^T{x}^{\left(i\right)}\right)}=P\left(y^{\left(i\right)}=l|x^{\left(i\right)};\theta \right)x^{\left(i\right)}$$
因此损失函数的导数为：
$$\begin{gathered} \frac{\partial J\left(\theta \right)}{\partial {\theta }_l}=\sum _{i=1}^m\left[P\left(y^{\left(i\right)}=l|x^{\left(i\right)};\theta \right)x^{\left(i\right)}-I\left\{y^{\left(i\right)}=l\right\}{x}^{\left(i\right)}\right] \\ =\sum _{i=1}^m\left[P\left(y^{\left(i\right)}=l|x^{\left(i\right)};\theta \right)-I\left\{y^{\left(i\right)}=l\right\}\right]x^{\left(i\right)} \end{gathered}$$
这样，梯度下降法的核心步骤就是：
$${\theta }_l⟵{\theta }_l-\alpha \sum _{i=1}^m\left[P\left(y^{\left(i\right)}=l|x^{\left(i\right)};\theta \right)-I\left\{y^{\left(i\right)}=l\right\}\right]x^{\left(i\right)}$$

---

3. 代码实现

​Softmax 回归类：

import numpy as np

class Softmax(object):
    theta = 0  # 参数
    
    def __h(self,x):
        h = np.empty(self.theta.shape[0])
        for i in range(h.shape[0]):
            h[i] = np.exp(np.dot(self.theta[i], x))
        h = h / h.sum()  # 归一化
        return h
    
    def __GD(self,X, y):
        X = np.insert(X, 0, 1, axis = 1)
        alpha = 0.1
        iter_num = 0
        while True:
            tmp = self.theta.copy()
            
            H = np.empty(X.shape)
            for i in range(X.shape[0]):
                H[i] = self.__h(X[i])
                
            for k in range(tmp.shape[0]):
                for i in range(X.shape[0]):
                    tmp[k] = tmp[k] - alpha * (H[i,k] - (y[i]==k)) * X[i]
            if np.allclose(self.theta, tmp, rtol = 1e-3):
                break
            self.theta = tmp.copy()
            iter_num += 1
        print("迭代次数：",iter_num)
    
    def fit(self, X, y):
        self.theta = np.zeros([np.max(y) + 1, X.shape[1] + 1])
        self.__GD(X, y) # 只给出了梯度下降法
    
    def predict(self, X):
        X = np.insert(X, 0, 1, axis = 1)
        y_pred = np.empty(X.shape[0])
        for i in range(y_pred.shape[0]):
            y_pred[i] = np.argmax(self.__h(X[i]))
        return y_pred

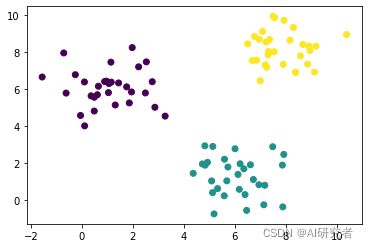
​使用该算法来看一个实例：

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.metrics import confusion_matrix

# 创造三类数据，数据标签是{0, 1, 2}
X, y = make_blobs(90, 2,random_state=0,
                  centers=[[1,6],[6,1],[8,8]])
plt.scatter(X[:,0],X[:,1],c=y)

clf = Softmax()
clf.fit(X, y) # 训练

# 作出区域预测图
x1,x2=np.mgrid[-2:12:0.1,-2:12:0.1]
X_test=np.stack([x1.flat,x2.flat],axis=1)
y_pred = clf.predict(X_test)
y_pred = y_pred.reshape(x1.shape)
plt.pcolormesh(x1,x2,y_pred,alpha=0.2)
plt.show()

​上述数据可视化后是这样的：

在代码中，输出变量 $y$ 的取值为 $\left\{0,1,2\right\}$ ，与上面的算法稍微有所不同，很多编程语言的序列下标都是从 $0$ 开始计数的，输出变量 $y$ 从 $0$ 开始也是比较方便的。运行代码训练后，迭代次数为 $24$ ，可视化：

​可以看到算法将所有训练数据正确分类，不过也可以看到一点，在黄色类别附近再多给几个点，算法有可能将其错误分类。

---

总结

​Softmax 回归是一种多分类的算法，它可以说是 Logistic 回归的推广，本篇文章中就将其和 Logistic 回归作对比。它也可以使用广义线性模型进行推导。