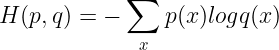softmax回归详解

在一些其他场景中，我们的模型输出可能是一个图像类别这样的离散值，对于这样的离散值预测问题，可以使用 softmax 回归的分类模型。

1.1 分类问题

在一个简单图像分类问题中，输入图像的高和宽均是 2 像素，色彩为灰度，可以将图像中的 4 像素分别记为   ，假设训练集中图像的真实标签为狗、猫和鸡，也就是说通过这4种像素可以表示出这三种动物，这些标签对应着  。

1.2 softmax回归模型 

softmax回归和线性回归一样也是将输入特征与权重做线性叠加，但是softmax回归的输出值个数等

于标签中的类别数，对每个输入计算出输出：

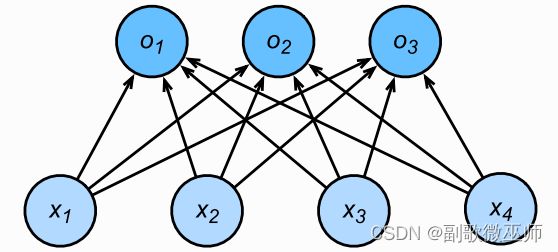
 softmax回归是单层神经网络，每个输出的计算依赖于所有的输入

 

那么如何将输出的结果转换成对应的类别呢？ 首先可以将输出值  中最大的输出所对应的类作为预测输出，例如 ，， 分别为 0.1，10，0.1，由于  最大 ，那么预测类别为 2 ，代表猫。

但是输出层的输出值的范围是不确定的，并且真实标签是离散值，难以计算出与输出值的误差。

softmax运算符解决了这些问题，通过下式将输出值变换成值为正并且和为 1 的概率分布：

其中

 

可以看出   ，且都小于1，若 ，无论剩余两个值是多少，图像类别是猫的概率为 80%。

1.3 小批量样本分类矢量计算表达式

给定一个小批量样本，批量大小为  ，输入特征数为  ，输出类别数为  ，设批量特征是，softmax 回归的权重和偏置为 ，计算表达式为：

1.4 交叉熵损失函数

可以使用线性回归那样的平方损失函数    但是想要预测分类结果正确，我们其实并不需要预测概率完全等于标签概率，只需要其中一个预测值比其他的都大就行了，即使  不管其他两个预测值为多少，类别预测均正确，而平方损失则过于严格。

交叉熵刻画的是两个概率分布之间的距离， 代表正确答案， 代表的是预测值，交叉熵越小，两个概率的分布越接近。

其中  为标签值， 为预测值

2.1获取数据集

在 softmax 中使用Fashion-MNIST数据集

导入需要的包

%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l

d2l.use_svg_display()

通过torch框架内置函数下载Fashion-MNIST数据集并读取到内存中

trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(
    root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
    root="../data", train=False, transform=trans, download=True)

该数据集中包含10个类别的图像，每个类别由训练集中的6000张图像和测试集中的1000张图像组成，训练集和测试集分别包含60000和10000张图像。

len(mnist_train), len(mnist_test)

(60000, 10000)

每个输入图像的高度和宽度均为28像素

torch.Size([1, 28, 28])

Fashion-MNIST中包含的10个类别，分别为t-shirt（T恤）、trouser（裤子）、pullover（套衫）、dress（连衣裙）、coat（外套）、sandal（凉鞋）、shirt（衬衫）、sneaker（运动鞋）、bag（包）和ankle boot（短靴）。

以下函数用于在数字标签索引及其文本名称之间进行转换。

def get_fashion_mnist_labels(labels):  #@save
    """返回Fashion-MNIST数据集的文本标签"""
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]

创建一个函数来可视化这些样本。

def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):  #@save
    """绘制图像列表"""
    figsize = (num_cols * scale, num_rows * scale)
    _, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)
    axes = axes.flatten()
    for i, (ax, img) in enumerate(zip(axes, imgs)):
        if torch.is_tensor(img):
            # 图片张量
            ax.imshow(img.numpy())
        else:
            # PIL图片
            ax.imshow(img)
        ax.axes.get_xaxis().set_visible(False)
        ax.axes.get_yaxis().set_visible(False)
        if titles:
            ax.set_title(titles[i])
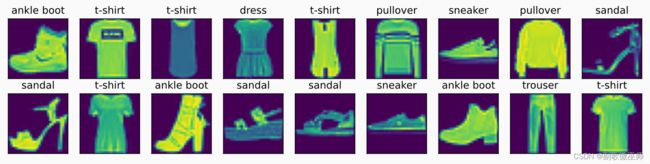
    return axes

展示训练集中前几个样本的图像以及标签

X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))
show_images(X.reshape(18, 28, 28), 2, 9, titles=get_fashion_mnist_labels(y));

 2.2读取小批量数据

batch_size = 256

def get_dataloader_workers():  #@save
    """使用4个进程来读取数据"""
    return 4

train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,
                             num_workers=get_dataloader_workers())

PyTorch 的 DataLoader 中一个很方便的功能是允许用多进程来加速数据读取 。这里我们 设置 4 个进程读取数据。

2.3 初始化模型参数

import torch
from IPython import display
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

原始数据集中的每个样本都是28×28的图像，我们将展平每个图像，把它们看作长度为784的向量，在softmax回归中，我们的输出与类别一样多。因为我们的数据集有10个类别，所以网络输出维度为10。 因此，权重将构成一个784×10的矩阵， 偏置将构成一个1×10的行向量。

num_inputs = 784
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

2.4 实现softmax运算

def softmax(X):
 X_exp = X.exp()
 partition = X_exp.sum(dim=1, keepdim=True)
 return X_exp / partition

2.5 定义模型

def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

2.6 定义损失函数

def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])

cross_entropy(y_hat, y)

2.7 计算分类精度

当预测值与标签分类一致时，那么就是正确的。分类精度即正确预测数量与总预测数量之比。所以我们使用argmax获得每行中最大元素的索引来获得预测类别，然后将预测类别与真实标签进行比较。

def accuracy(y_hat, y):  #@save
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

2.8训练模型

和线性回归类似，同样使用小批量随机梯度下降来优化模型的损失函数。

 

num_epochs, lr = 5, 0.1
# 本函数已保存在d2lzh包中⽅便以后使⽤
def train_ch3(net, train_iter, test_iter, loss, num_epochs,
batch_size,params=None, lr=None, optimizer=None):
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            y_hat = net(X)
            l = loss(y_hat, y).sum()
 
 # 梯度清零
            if optimizer is not None:
                optimizer.zero_grad()
            elif params is not None and params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()
 
            l.backward()
            if optimizer is None:
                 d2l.sgd(params, lr, batch_size)
            else:
                 optimizer.step() 
            train_l_sum += l.item()
            train_acc_sum += (y_hat.argmax(dim=1) ==y).sum().item()
            n += y.shape[0]
        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'% (epoch + 1, train_l_sum / n,
        train_acc_sum / n,test_acc))
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs,
batch_size, [W, b], lr)

epoch 1, loss 0.7878, train acc 0.749, test acc 0.794
epoch 2, loss 0.5702, train acc 0.814, test acc 0.813
epoch 3, loss 0.5252, train acc 0.827, test acc 0.819
epoch 4, loss 0.5010, train acc 0.833, test acc 0.824
epoch 5, loss 0.4858, train acc 0.836, test acc 0.815

2.9 预测

训练完成后，现在就可以演示如何对图像进行分类了。给定⼀系列图像（第三行图像输出），我们比较⼀下它们的真实标签（第⼀行文本输出）和模型预测结果（第二行文本输出）。

X, y = iter(test_iter).next()
true_labels = d2l.get_fashion_mnist_labels(y.numpy())
pred_labels =
d2l.get_fashion_mnist_labels(net(X).argmax(dim=1).numpy())
titles = [true + '\n' + pred for true, pred in zip(true_labels,
pred_labels)]
d2l.show_fashion_mnist(X[0:9], titles[0:9])