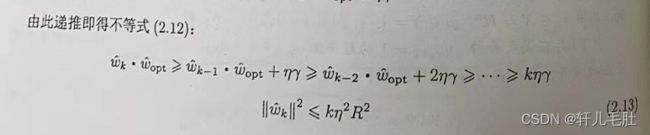感知机（perceptron）

        本内容首先介绍感知机简述；然后介绍感知机模型；接着叙述感知机的学习策略，特别是损失函数；最后介绍感知机学习算法，包括原始形式和对偶形式，并证明算法的收敛性。

目录

一、简述

二、感知机模型 

三、感知机学习策略

（一）数据集的线性可分性 

（二）感知机学习策略

四、感知机学习算法 

（一）感知机学习算法的原始形式

 1、原理

 2、算法描述

3、主要实现代码

（二） 感知机学习算法的对偶形式

1、原理

2、算法描述 

3、主要实现代码

（三）算法收敛性

（四）原始形式和对偶形式的选择

五、实例

六、鸢尾花数据进行实现感知机算法 

---

一、简述

        感知机（perceptron）是二分类的线性分类模型，属于监督学习算法。输入为实例的特征向量，输出为实例的类别（取+1和-1）。感知机旨在求出将训练数据进行线性划分的分离超平面。为求得超平面，感知机导入了基于误分类的损失函数，利用梯度下降法对损失函数进行最优化求解，求得感知机模型。

        感知机学习算法具有简单而易于实现的优点，分为原始形式和对偶形式，感知机预测是学习得到的感知机模型对于新的输入实例进行分类。感知机是由美国学者Frank Rosenblatt在1957年提出来的。因为感知机也是作为神经网络（深度学习）的起源的算法。因此，学习感知机的构造也就是学习通向神经网络和深度学习的一种重要思想。

二、感知机模型 

如图2.1所示。

图2.1 感知机模型

         感知机学习由训练数据集（实例的特征向量及类别）T={(x1,y1),(x2,y2),...,(xn,yn)}

其中，

 求得感知机模型（式（1）），即求得模型参数w，b。感知机预测通过学习得到的感知机模型，对新的输入实例给出其对应的输出类别。

三、感知机学习策略

（一）数据集的线性可分性 

 如果训练数据集是线性可分的，则感知机一定能求得分离超平面。

 如果是非线性可分的数据，则无法获得超平面。

（二）感知机学习策略

        假设训练数据集是线性可分的，感知机学习的目标式求得一个能够将训练数据集正实例点和负实例点完全正确分开的分离超平面。为了找到这样的超平面，即确定感知机模型参数w、b，需要确定一个学习策略，即定义（经验）损失函数，并将损失函数极小化。

        损失函数的一个自然选择是误分类点的总数，但是这样的函数不是参数w，b的连续可导函数，不易优化。损失函数的另一个选择是误分类点到超平面S的总距离，这是感知机所采用的。

矩阵范数：描述向量引起变化的大小（AX=B -->矩阵X变化了A个量级后成了B）

向量范数（L-P范数）：描述向量在空间中的大小（描述两个量之间的距离关系）

L0范数：用来统计向量中非0元素个数

L1范数：向量中所有元素的绝对值之和

L2范数：欧式距离

范数：计算向量中的最大值

四、感知机学习算法 

（一）感知机学习算法的原始形式

 1、原理

        至此，感知机学习问题就转化为了求解损失函数的最优化问题。

        由于感知机学习算法是误分类驱动的，这里基于随机梯度下降法（SGD）进行优化求解。即任意选取一个超平面w0，b0，然后用梯度下降法不断地极小化损失函数。极小化过程中不是一次使M中的所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。

        这里不能使用基于所有样本的批量梯度下降（BGD）进行优化。这是因为我们的损失函数里面有限定，只有误分类的M集合里面的样本才能参与损失函数的优化。所以我们不能用最普通的批量梯度下降，只能采用随机梯度下降（SGD）或者小批量梯度下降（MBGD）。

 2、算法描述

        这种学习算法直观上有如下解释： 当一个实例点被误分类，即位于分离超平面的错误一侧时，则调整w，b的值，使分离超平面向该误分类点的一侧移动，以减少该误分类点与超平面间的距离，直至超平面越过该误分类点使其被正确分类。 

3、主要实现代码

def fit(self, X, y):
    # 初始化参数w，b
    self.w = np.zeros(X.shape[1])
    self.b = 0
    # 记录所有error
    self.errors_ = []
    for _ in range(self.n_iter):
        errors = 0
        for xi, yi in zip(X, y):
            update = self.eta * (yi - self.predict(xi))
            self.w += update * xi
            self.b += update
            errors += int(update != 0.0)
        if errors == 0:
            break
        self.errors_.append(errors)

    return self

（二） 感知机学习算法的对偶形式

1、原理

2、算法描述 

3、主要实现代码

def fit(self, X, y):
    """
    对偶形态的感知机
    由于对偶形式中训练实例仅以内积的形式出现
    因此，若事先求出Gram Matrix，能大大减少计算量
    """
    # 读取数据集中含有的样本数,特征向量数
    n_samples, n_features = X.shape
    self.alpha, self.b = [0] * n_samples, 0
    self.w = np.zeros(n_features)
    # 计算Gram_Matrix
    self.calculate_g_matrix(X)

    i = 0
    while i < n_samples:
        if self.judge(X, y, i) <= 0:
            self.alpha[i] += self.eta
            self.b += self.eta * y[i]
            i = 0
        else:
            i += 1

    for j in range(n_samples):
        self.w += self.alpha[j] * X[j] * y[j]

    return self

（三）算法收敛性

        现在证明，对于线性可分数据集，感知机学习算法原始形式收敛，即经过有限次迭代可以得到一个将训练数据集完全正确划分的分类超平面及感知机模型。        

         定理表明，误分类的次数k是有上界的，经过有限次搜索可以找到将训练数据完全正确分开的分离超平面。也就是说，当训练数据集线性可分时，感知机学习算法原始形式迭代是收敛的。但同时感知机学习算法存在许多解，这些解既依赖于初值的选择，也依赖于迭代过程中误分类点的选择顺序。为了得到唯一的超平面，需要对分离超平面增加约束条件。当训练数据集线性不可分时，感知机学习算法不收敛，迭代结果会发生振荡。

        我们大概从下图看出感知机的训练过程：

线性可分的过程：

 

线性不可分的过程：

 

（四）原始形式和对偶形式的选择

• 如果特征数过高，计算内积非常耗时，应选择对偶形式算法加速。
• 如果样本数过多，每次计算累计和就没有必要，应选择原始算法。

五、实例

        假设我们有三个训练样本，每个样本只有两维特征。在三个样本中，正样本有两个，分别为：，，负样本有一个，为：，题目要求是，求出能将正负样本分开的感知机模型。由于特征空间是二维的，所以我们可以很容易地将三个样本点在坐标系中表示出来（如下图所示）。很明显，这三个样本是线性可分的，即我们可以将感知机的损失函数训练至0。 

六、鸢尾花数据进行实现感知机算法 

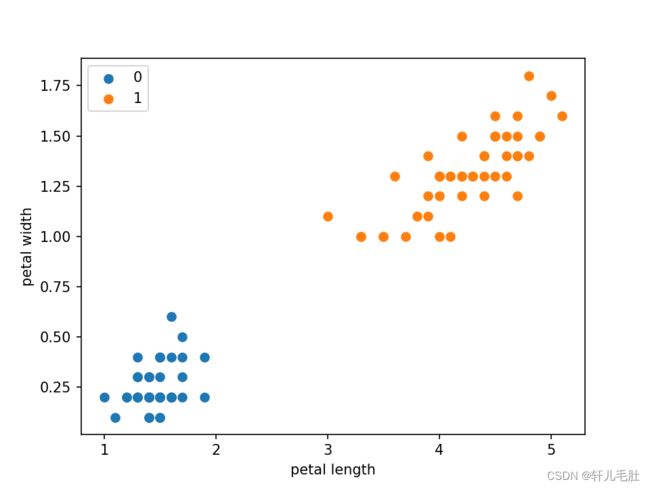
        简单介绍下鸢尾花数据：iris数据集的中文名是安德森鸢尾花卉数据集，英文全称是Anderson’s Iris data set。iris数据集是一个150行5列的二维表。具体来说是150个样本，每个样本是数据集中的每行数据，每个样本有4个特征（前4列），1个标签（第五列）。4个特征分别是花萼长度、花萼宽度、花瓣长度、花瓣宽度，标签共有3个，分别是山鸢尾、变色鸢尾还是维吉尼亚鸢尾。

        目标是建立一个分类器，通过样本的四个特征判断样本属于哪个品种。

1.首先查看数据集内容和详细信息：

from sklearn import datasets
iris = datasets.load_iris()
 
print(iris.data.shape) #数据集大小
print(iris.data[:5])  #查看数据集前5行
print(iris.target.shape)  #数据集标签大小
print(iris.target)       #查看数据集的标签

 2.创建DataFrame，读取数据

import pandas as pd
from sklearn.datasets import load_iris
 
iris = load_iris()
df = pd.DataFrame(iris.data,columns=iris.feature_names)  #iris.data数据集大小作为行索引，列是数据集的特征
df['label'] = iris.target  #增加label列，值是数据标签

3.直接实现感知机

#选择4个特征作为训练
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
plt.scatter(df[:50]['petal length'],df[:50]['petal width'],label='0')
plt.scatter(df[50:100]['petal length'],df[50:100]['petal width'],label='1')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend()
plt.show()
 
#实现感知机
#取2,3两列特征，-1表示标签
data = np.array(df.iloc[:100, [2, 3, -1]])
X = data[:,:-1]  #取出特征
y = data[:,-1]   #取出标签
 
y = np.array([1 if i==1 else -1 for i in y])   #y表示类别，正常取值是0和1，把0类别的值改为-1
 
class Model():
    def __init__(self):
        #一共训练两个特征需要2个权重参数，data数据是3列，第三列是数据标签
        self.w = np.ones(len(data[0])-1,dtype=np.float32) 
        self.b = 0
        self.l_rate = 0.1
        
    def sign(self,x,w,b):
        y = np.dot(x,w) + b
        return y
    #使用随机梯度进行拟合
    def fit(self,X_train,y_train):
        is_wrong = False
        while not is_wrong:
            wrong_count = 0
            for d in range(len(X_train)):
                X = X_train[d]
                y = y_train[d]
                #如果分类错误,就进行梯度更新
                if y*self.sign(X, self.w, self.b) <= 0:
                    self.w = self.w + self.l_rate * np.dot(y,X)
                    self.b = self.b + self.l_rate * y
                    wrong_count += 1
            
            if wrong_count == 0:  #如果全都分类正确,wrong_count值为0,则停止拟合
                is_wrong = True
        return 'Perceptron Model'
    
    def score(self):
        pass
    
#拟合
perceptron = Model()
perceptron.fit(X,y)
 
print('权重:', perceptron.w[0], perceptron.w[1])
print('偏置:', perceptron.b)
#可视化结果
x_points = np.linspace(-3, 7,10)
y_ = -(perceptron.w[0]*x_points + perceptron.b)/perceptron.w[1]
plt.plot(x_points, y_)  #绘制训练出的超平面
 
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')  #前50行，第0列是petal length
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend()

 权重: 0.13999999999999987 0.8899999999999998
偏置: -0.7999999999999999

 4.使用sklearn构造感知机

import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.linear_model import Perceptron
 
iris = load_iris()
df = pd.DataFrame(iris.data,columns=iris.feature_names)  
df['label'] = iris.target
 
#选择4个特征作为训练
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
plt.scatter(df[:50]['petal length'],df[:50]['petal width'],label='0')
plt.scatter(df[50:100]['petal length'],df[50:100]['petal width'],label='1')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend()
plt.show()
 
#实现感知机
#取2,3两列特征，-1表示标签
data = np.array(df.iloc[:100, [2, 3, -1]])
X = data[:,:-1]  #取出特征
y = data[:,-1]   #取出标签
y = np.array([1 if i==1 else -1 for i in y])   #y正常取值是0和1，把0类别的值改为-1
 
#fit_intercept参数：False状态截距是0，True状态截距学习得到，设置成False会出错
 
clf = Perceptron(fit_intercept=True, max_iter=100, shuffle=True)
clf.fit(X,y)
 
#输出权重,偏置
print('权重:',clf.coef_)
print('偏置:',clf.intercept_)
 
#可视化结果
x_points = np.linspace(-3, 7,10)
y_ = -(clf.coef_[0][0]*x_points + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_points, y_)  #绘制训练出的超平面
 
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')  #前50行，第0列是petal length
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend()

 

 参考文献：

1、李航《机器学习方法》

2、感知机（Perceptron）

3、感知机原理小结

4、【机器学习】感知机原理详解

5、感知机原理（Perceptron）

6、感知机基本形式和对偶形式实现

7、感知机算法python实现