【leetcode热题100】刷题记录（5-8）

5. 最长回文子串

题目链接

给你一个字符串 s，找到 s 中最长的回文子串。

 
 
题目解答

思路就是动态规划。
状态定义：dp[i][j]表示字符串从i到j的字符串是否是回文串
状态转移：
s[i] == s[j] 分两种，一种长度小于等于3， dp[i][j]==True；其他情况则dp[i][j] = dp[i+1][j-1];

s[i] != s[j] 则dp[i][j] = False;

python 解答

class Solution:
    def longestPalindrome(self, s: str) -> str:
        n = len(s)
        # 初始化dp数组
        dp = [[False]*(n) for _ in range(n)]
        # 边界条件 单个字符是属于回文字符串的
        for i in range(n): dp[i][i] = True
        # 定义一下最长长度和初始位置
        maxlen, idx = 1, 0
        # 按照长度来遍历
        for lens in range(2, n + 1):
            for st in range(0, n - lens + 1):
                end = st + lens - 1

                if s[st] == s[end]: # 字符相等的时候，看长度， 分两种情况
                    if lens <= 3:
                        dp[st][end] = True
                    else:
                        dp[st][end] = dp[st+1][end-1]
                else: # 字符不相等的时候，必然不是
                    dp[st][end] = False
                
                # 更新一下最优状态
                if dp[st][end] and lens > maxlen:
                    maxlen = lens
                    idx = st

        return s[idx:idx+maxlen]

cpp解答

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        if (n < 2) {
            return s;
        }

        int maxLen = 1;
        int begin = 0;

        vector<vector<bool>> dp(n, vector<bool>(n));
        for (int i = 0; i < n; i ++) dp[i][i] = true;

        for (int l = 2; l <= n; l ++)
        {
            for (int i = 0; i < n; i ++)
            {
                int j = i + l - 1;
                if (j >= n) break;
                if (s[i] == s[j])
                {
                    if (l <= 3) dp[i][j] = true;
                    else dp[i][j] = dp[i+1][j-1];
                }
                else
                {
                    dp[i][j] = false;
                }
				
				// 更新最优状态
                if (dp[i][j] && l > maxLen)
                {
                    maxLen = l;
                    begin = i;
                }
            }

        }

        return s.substr(begin, maxLen);
    }
};

2. 两数相加

题目链接

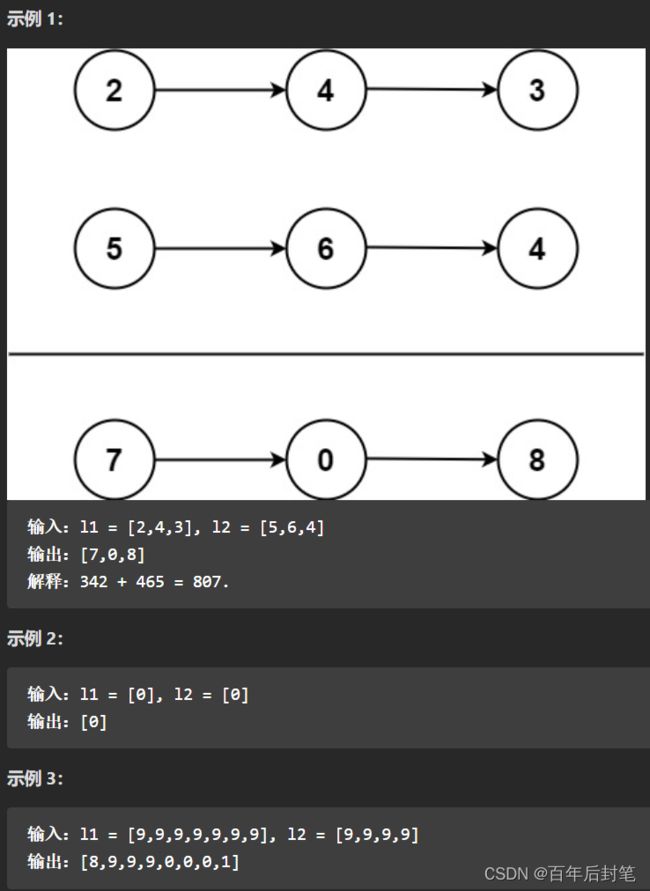
给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

 
 
题目解答

直接模拟就可以了，注意c++用的时候，返回对象是个指针还是一个对象，指针的话，要用->，对象用.。

python 解答

class Solution(object):
    def addTwoNumbers(self, l1, l2):
        """
        :type l1: ListNode
        :type l2: ListNode
        :rtype: ListNode
        """
        adds = 0 # 进位
        head = curr = ListNode(0)
        while l1 or l2 or adds:
            val = 0
            if l1: 
                val += l1.val
                l1 = l1.next
            if l2: 
                val += l2.val
                l2 = l2.next
            val, adds = (val + adds) % 10, (val + adds) // 10 
            node = ListNode(val)
            curr.next = node
            curr = curr.next
        return head.next

cpp解答

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        int adds = 0;
        ListNode *head = nullptr;
        ListNode *curr = nullptr;
        head = curr = new ListNode(0);
        while (l1 || l2 || adds)
        {
            int val = 0;
            if(l1)
            {
                val += l1->val;
                l1 = l1->next;
            }
            if(l2)
            {
                val += l2->val;
                l2 = l2->next;
            }
            curr->next = new ListNode((val + adds) % 10);
            adds = (val + adds) / 10;
            curr = curr->next;
        }
        return head->next;
    }
};

3. 无重复字符的最长子串

题目链接

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

 
 
题目解答

双指针加set

从左往右滑窗，如果遇到set里面没有的元素，右指针一直右移动，直到不满足了，更新一下最长距离，然后加入s[r]，删掉s[l]，这里我还记录了final_l，相当于如果要求最长不重复子序列的话，那就直接输出s[final_l:final_l+res]

python 解答

class Solution(object):
    def lengthOfLongestSubstring(self, s):
        """
        :type s: str
        :rtype: int
        """
        l, r = 0, 0
        final_l = 0
        res = 0
        dic = set()
        while r < len(s):
            while r < len(s) and s[r] not in dic:
                dic.add(s[r])
                r += 1
            if r - l > res:
                res = r - l
                final_l = l
            dic.remove(s[l])
            l += 1
        return res

cpp解答

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int l = 0, r = 0, res = 0, final_l;
        unordered_set<char> dic;
        while (r < s.size())
        {
            while (r < s.size() and dic.find(s[r]) == dic.end())
            {
                dic.insert(s[r]);
                r ++;
            }

            if (r - l > res)
            {
                res = r - l;
                final_l = l;
            }

            dic.erase(s[l]);
            l ++;

        }
        return res;
    }
};

4. 寻找两个正序数组的中位数

题目链接

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

 
 
题目解答

二分查找

具体而言就是寻找到对两个数组的一个分割，转化成求前k小数字的问题，分割的时候主要使得分割线左右元素的值满足交叉有序关系，然后再讨论一些边界条件即可。具体的可以看官网解析

python 解答

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        if len(nums1) > len(nums2):
            return self.findMedianSortedArrays(nums2, nums1)

        infinty = 2**40
        m, n = len(nums1), len(nums2)
        left, right = 0, m
        # median1：前一部分的最大值
        # median2：后一部分的最小值
        median1, median2 = 0, 0

        while left <= right:
            # 前一部分包含 nums1[0 .. i-1] 和 nums2[0 .. j-1]
            # // 后一部分包含 nums1[i .. m-1] 和 nums2[j .. n-1]
            i = (left + right) // 2
            j = (m + n + 1) // 2 - i

            # nums_im1, nums_i, nums_jm1, nums_j 分别表示 nums1[i-1], nums1[i], nums2[j-1], nums2[j]
            nums_im1 = (-infinty if i == 0 else nums1[i - 1])
            nums_i = (infinty if i == m else nums1[i])
            nums_jm1 = (-infinty if j == 0 else nums2[j - 1])
            nums_j = (infinty if j == n else nums2[j])

            if nums_im1 <= nums_j:
                median1, median2 = max(nums_im1, nums_jm1), min(nums_i, nums_j)
                left = i + 1
            else:
                right = i - 1

        return (median1 + median2) / 2 if (m + n) % 2 == 0 else median1

cpp解答

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        if (nums1.size() > nums2.size()) {
            return findMedianSortedArrays(nums2, nums1);
        }
        
        int m = nums1.size();
        int n = nums2.size();
        int left = 0, right = m;
        // median1：前一部分的最大值
        // median2：后一部分的最小值
        int median1 = 0, median2 = 0;

        while (left <= right) {
            // 前一部分包含 nums1[0 .. i-1] 和 nums2[0 .. j-1]
            // 后一部分包含 nums1[i .. m-1] 和 nums2[j .. n-1]
            int i = (left + right) / 2;
            int j = (m + n + 1) / 2 - i;

            // nums_im1, nums_i, nums_jm1, nums_j 分别表示 nums1[i-1], nums1[i], nums2[j-1], nums2[j]
            int nums_im1 = (i == 0 ? INT_MIN : nums1[i - 1]);
            int nums_i = (i == m ? INT_MAX : nums1[i]);
            int nums_jm1 = (j == 0 ? INT_MIN : nums2[j - 1]);
            int nums_j = (j == n ? INT_MAX : nums2[j]);

            if (nums_im1 <= nums_j) {
                median1 = max(nums_im1, nums_jm1);
                median2 = min(nums_i, nums_j);
                left = i + 1;
            } else {
                right = i - 1;
            }
        }

        return (m + n) % 2 == 0 ? (median1 + median2) / 2.0 : median1;
    }
};