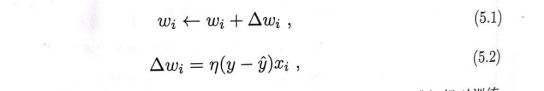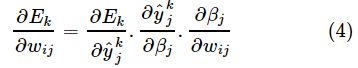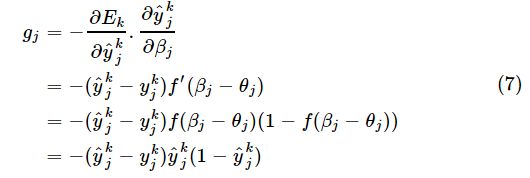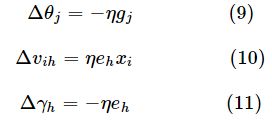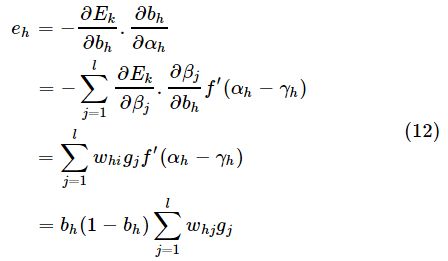1）神经元模型
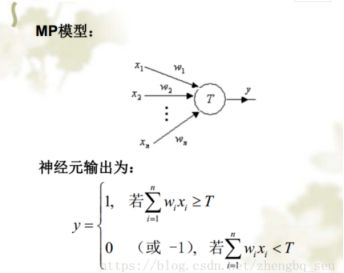
最简单的MP模型，右图是“与”逻辑的数学表达：
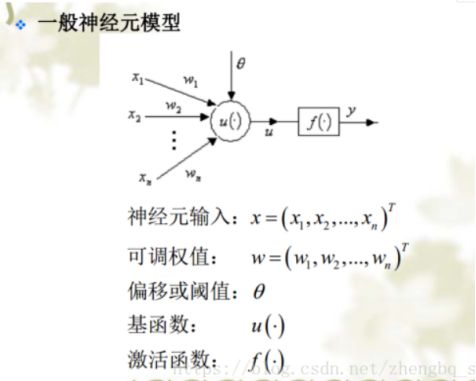
神经元模型
基函数表示“如何组合”
激活函数表示“是否到阈值”
“最后网络表达的方式”
基函数类型1：线性函数
给定训练集，权重wi以及阈值θ可通过学习得到。阈值可看做一个固定输入为-1.0的“哑结点”所对应连接权重w（n+1），这样权重和阈值的学习就可以统一为权重的学习。感知机学习规则非常简单，对训练样例（x，y），若当前感知机的输出为y’，则感知机权重将这样调整：
其中，被称为学习率，若感知机对训练样例（x，y）预测正确，即y’=y，则感知机不会再发生变化，否则将根据错误的程度对权重进行调整。
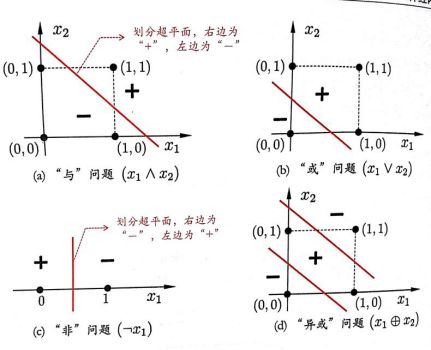
关于线性可分问题：感知机只有输出神经元进行F函数处理，学习能力十分有限，实际上，与、或、非问题等都是线性可分的，存在一个线性超平面能将他们划分（超平面将空间分成两部分，一部分大于0，一部分小于0），对于该种线性超平面问题，感知机学习过程一定会收敛，否则感知机就会发生震荡，不能求得合适解。
要解决非线性可分问题，使用多层功能神经元：
我们知道神经网络里面有很多的层，每一层又有很多的神经元。看起来就非常复杂，似乎输入与输出都很凌乱，对它的理解也很难。那么我们可以从单个神经元入手，考虑单个神经元的输入与输出之间的关系，再扩展到整个神经网络。
从图中可以得到：
hθ(x)=g(−30+20x1+20x2)
hθ(x)=g(−30+20x1+20x2)
假如x1和x2的组合如下：
x1 x2 y
0 0 0
0 1 0
1 0 0
1 1 1
我们将x1和x2输入到假设函数，可以得到：
g(-30+20*0+20*0)=g(-30)≈0
g(-30+20*0+20*1)=g(-10)≈0
g(-30+20*1+20*0)=g(-10)≈0
g(-30+20*1+20*1)=g(10)≈1
事实上，这就像是一个“与”操作。
那么对于“或”操作也是类似的。“或”操作的θ可以如下选择：
hθ(x)=g(−10+20x1+20x2)
hθ(x)=g(−10+20x1+20x2)
g(-10+20*0+20*0)=g(-10)≈0
g(-10+20*0+20*1)=g(10)≈1
g(-10+20*1+20*0)=g(10)≈1
g(-10+20*1+20*1)=g(30)≈1
可以看到，通过选择不同的θ值，就可以变成“或”操作。
那么对于复杂一点的操作，比如“异或”操作呢？
“异或”操作使用两层神经元。通过选择如图的参数，我们可以知道：
a(2)1，a1(2)神经元是一个“与”操作。a(2)2，a2(2)神经元是一个“非与”操作。a(3)1，a1(3)神经元是一个“或”操作。这三者的结合就可以得到“异或”操作了。
所以，经过一个神经元，其实就是在做一种判断，像“与”，“或”这种简单的逻辑。单个神经元就可以做到了，但是对于复杂的判断，就不是一个神经元就可以搞定的。随着复杂程度的增加，神经网络也就形成了。
其实这跟数字电路还有点像。以前学习数字电路的时候，也是从简单的与非门，或门等简单的逻辑电路学起，然后复杂的逻辑都是通过简单逻辑的组合得到的。
另外还有“单隐层网络”以及“多隐层前馈神经网络”，此处不再多说。
2）误差逆传递算法（BP算法）
误差逆传播算法是迄今最成功的神经网络学习算法，现实任务中使用神经网络时，大多使用BP算法进行训练。
给定训练集
即输入示例由d个属性描述，输出l个结果。如图所示，是一个典型的单隐层前馈网络，它拥有d个输入神经元、l个输出神经元、q个隐层神经元，其中，θj表示第j个神经元的阈值，γh表示隐层第hh个神经元的阈值，输入层第i个神经元与隐层第hh个神经元连接的权值是vih，隐层第h个神经元与输出层第j个神经元连接的权值是whj。
于是，按照神经网络的传输法则，隐层第h个神经元接收到的输入
，输出
，输出层j第个神经元的输入
，输出
，其中f函数是“激活函数”，γh和θj分别是隐藏层和输出层的阈值，选择Sigmoid函数作为激活函数。
对训练样例(xk,yk)，通过神经网络后的输出是
，则其均方误差为
为了使输出的均方误差最小，我们以均方误差对权值的负梯度方向进行调整，给定学习率η，
这里为什么是取负梯度方向呢？因为我们是要是均方误差最小，而
w的更新估计式为
如果，
，则表明减小w才能减小均方误差，所以Δw应该小于零，反之，如果
,则表明增大w的值可以减小均方误差，所以所以Δw应该大于零，所以在这里取负的偏导，以保证权值的改变是朝着减小均方误差的方向进行。
在这个神经网络中，Ek是有关
的函数，
是有关βj的函数，而βj是有关wij的函数，所以有
而
而对Sigmoid函数有
所以
将式(7)代入式(3)和式(4),就得到BP算法中关于Δwij的更新公式
类似可得：
其中，式(10)和式(11)中
至此，误差逆传播算法的推导已经完成，我们可以回过头看看，该算法为什么被称为误差逆传播算法呢？误差逆传播，顾名思义是让误差沿着神经网络反向传播，根据上面的推导
，其中
，是输出误差，
是输出层节点的输出y对于输入β的偏导数，可以看做是误差的调节因子，我们称gj为“调节后的误差”；而
所以eh可以看做是“调节后的误差”gj通过神经网络后并经过调节的误差，并且我们可以看出：权值的调节量=学习率x调节后的误差x上层节点的输出，算是对于误差逆向传播法表面上的通俗理解，有助于记忆。
整个逆向误差传递算法工作流程：
需注意的是， BP 算法的目标是要最小化训练集D上的累积误差
但我们上面介绍的"标准 BP 算法"每次仅针对一个训练样例更新连接权和阔值，如果类似地推导出基于累积误差最小化的更新规则，就得到了累积误差逆传算法累积 BP 算法与标准 BP 算法都很常用.一般来说，标准 BP 算法每次更新只针对单个样例，参数更新得非常频繁，而且对不同样例进行更新的效果可能出现"抵消"现象.因此，为了达到同样的累积误差极小点 标准 BP 算法往往需进行更多次数的法代.累积 BP 算法直接针对累积误差最小化，它在 卖取整个训练集 一遍后才对参数进行更新，其参数更新的频率低得多.但在很多任务中，累积误差下降到一定程度之后，进一步下降会非常缓慢，这时标准 BP 往往会更快获得较好的解，尤其是在训练非常大时更明显。
全局最小与局部最小：通过学习，我们知道，因为训练神经网络有个过程:
<1>Sample 获得一批数据；
<2>Forward 通过计算图前向传播，获得loss；
<3>Backprop 反向传播计算梯度，这个梯度能告诉我们如何去调整权重，最终能够更好的分类图片；
<4>Update 用计算出的梯度去更新参数
用一段伪码表述上述文字：
while True:
data_batch = dataset.sample_data_batch()
loss = network.forward(data_batch)
dx = network.backward()
x += - learninng_rate * dx
当我们谈论参数更新时，指的是上述伪码的最后一行，我们所要讨论的就是如何把这一行的更新迭代做的高级一点。梯度下降算法是深度学习中使用非常广泛的优化算法，也是众多机器学习算法中最常用的优化方法。几乎当前每一个先进的(state-of-the-art)机器学习库或者深度学习库都会包括梯度下降算法的不同变种实现。但是，它们就像一个黑盒优化器，很难得到它们优缺点的实际解释。
- 批量梯度下降（Batch gradient descent）
旨在每次使用全量的训练集样本来更新模型参数，即：θ=θ−η⋅∇θJ(θ) 伪码如下：
nb_epochs是用户输入的最大迭代次数。使用全量的训练集样本计算损失函数loss_function的梯度params_grad，然后使用学习速率learning_rate朝着梯度相反方向去更新模型的每一个参数params。
批量梯度下降每次学习都使用整个训练集，因此其优点在于每次更新都会朝着正确的方向进行，最后能够保证收敛于极值点(凸函数收敛于全局极值点，非凸函数可能会收敛于局部极值点，属于凸理论的问题了)，但是其缺点在于每次学习时间过长，并且如果训练集很大以至于需要消耗大量的内存，并且全量梯度下降不能进行在线模型参数更新。
- 随机梯度下降（Stochastic gradient descent）
旨在每次从训练集中随机选择一个样本来进行学习，即：θ=θ−η⋅∇θJ(θ;xi;yi)
伪码如下：
批量梯度下降算法每次都会使用全部训练样本，因此这些计算是冗余的，因为每次都使用完全相同的样本集。而随机梯度下降算法每次只随机选择一个样本来更新模型参数，因此每次的学习是非常快速的，并且可以进行在线更新。
特别观察一下SGD，红色的那条线，从图中可以看出SGD实际上是所有方法中最慢的一个，所以在实际中很少应用它，我们可以使用更好的方案。那我们来分析一下SGD的问题，是什么原因导致它的的速度这么慢？举个栗子：
我们可以从水平方向上可以看出，它的梯度很是非常小的，因为处于在一个比较浅的水平里；但是垂直有很大的速率，因为它是一个非常陡峭的函数，所以出现了这种状况：
在这种情况下使用SGD，在水平方向上进行比较缓慢，而在垂直方向上进展的很快，所以产生了很大的上下震荡。
- 小批量梯度下降（Mini-batch gradient descent）
旨在综合了 batch 梯度下降与 stochastic 梯度下降，在每次更新速度与更新次数中间取得一个平衡，其每次更新从训练集中随机选择 m,m
相对于随机梯度下降，Mini-batch梯度下降降低了收敛波动性，即降低了参数更新的方差，使得更新更加稳定。相对于全量梯度下降，其提高了每次学习的速度。并且其不用担心内存瓶颈从而可以利用矩阵运算进行高效计算。一般而言每次更新随机选择[50,256]个样本进行学习，但是也要根据具体问题而选择，实践中可以进行多次试验，选择一个更新速度与更次次数都较适合的样本数。mini-batch梯度下降可以保证收敛性，常用于神经网络中。