深度学习初级教程 2.深度神经网络

深度学习初级课程

• 1.单一神经元
• 2.深度神经网络
• 3.随机梯度下降法
• 4.过拟合和欠拟合
• 5.剪枝、批量标准化
• 6.二分类问题
• 应用.用TPU探测希格斯玻色子

---

正文

介绍

在这节课中，我们将看到我们如何构建能够学习复杂关系的神经网络——深层神经网络以其著名。
这里的关键思想是模块化，从简单的功能单元构建一个复杂的网络。我们已经了解了线性单元如何计算线性函数——现在我们将了解如何组合和修改这些单个单元，以建模更复杂的关系。

层

神经网络通常将神经元组织成层。当我们收集具有一组公共输入的线性单元时，我们得到一个密集层。
一个输入层中的三个圆与密集层中的两个圆相连。

两个线性单元的密集层，接收两个输入和一个偏置。

你可以认为神经网络中的每一层都在执行某种相对简单的转换。通过层层叠加，神经网络可以以越来越复杂的方式转换其输入。在一个训练有素的神经网络中，每一层都是一个变换，让我们更接近一个解决方案。

多种层次
Keras中的“层”是一种非常普遍的东西。从本质上讲，层可以是任何类型的数据转换。许多层，比如卷积层和循环层，通过使用神经元来转换数据，主要不同于它们形成的连接模式。其他的则用于特征工程或简单的算法。有一整个世界的层要发现-看看他们！

激活函数

然而，事实证明，两个致密层之间没有任何东西，并不比一个致密层本身好多少。致密层本身永远无法把我们带出线和平面的世界。我们需要的是非线性的东西。我们需要的是激活功能。

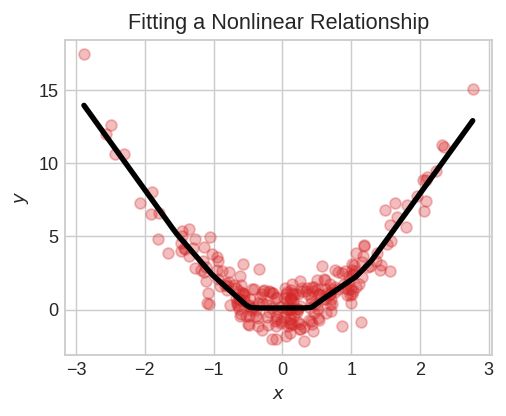
没有激活函数，神经网络只能学习线性关系。为了拟合曲线，我们需要使用激活函数。

激活函数就是我们应用于每一层输出（其激活）的函数。最常见的是整流函数max（0，x）。

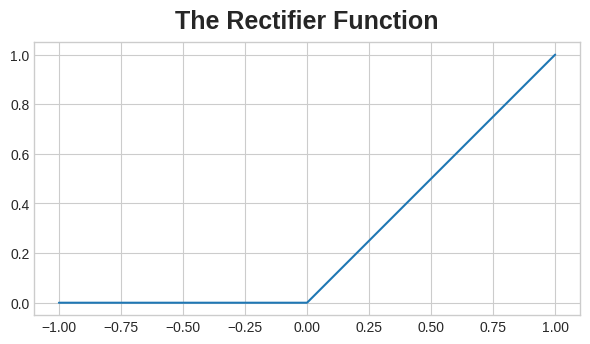
整流器功能图。当x>0时，线y=x，当x<0时，线y=0，形成“铰链”形状，如“/”。
整流器功能有一个图形，它是一条负部分“整流”为零的线。将该函数应用于神经元的输出将使数据弯曲，使我们远离简单的线条。

当我们把整流器连接到一个线性单元上时，我们得到一个整流的线性单元或ReLU。（因此，通常将整流器功能称为“ReLU功能”。）对线性单元应用ReLU激活意味着输出变为最大值（0，w*x+b），我们可以在如下图中绘制：
单个ReLU的示意图。就像一个线性单位，但我们现在有了一个铰链“/”，而不是“+”符号。

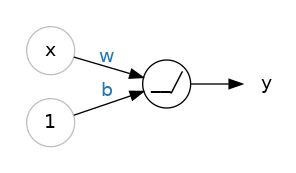
校正的线性单位。

堆积致密层

现在我们有了一些非线性，让我们看看如何堆叠层以获得复杂的数据转换。

一个输入层、两个隐藏层和最后一个线性层。
一堆密集的层构成一个“完全连接”的网络。
输出层之前的层有时被称为隐藏层，因为我们从未直接看到它们的输出。

现在，请注意，最后一个（输出）层是一个线性单元（意思是，没有激活函数）。这使得这个网络适用于回归任务，我们试图预测一些任意的数值。其他任务（如分类）可能需要在输出上使用激活函数。

建立序列模型

我们使用的顺序模型将按照从第一层到最后一层的顺序将一系列层连接在一起：第一层获得输入，最后一层产生输出。这将创建上图中的模型：

from tensorflow import keras
from tensorflow.keras import layers

model = keras.Sequential([
    # the hidden ReLU layers
    layers.Dense(units=4, activation='relu', input_shape=[2]),
    layers.Dense(units=3, activation='relu'),
    # the linear output layer 
    layers.Dense(units=1),
])

一定要把所有的图层放在一个列表中，比如[layer，layer，layer，…]，而不是作为单独的论点。要向层添加激活函数，只需在激活参数中给出其名称。

轮到你了

现在，为具体数据集创建一个深度神经网络。

---

练习部分

介绍

在本教程中，我们了解了如何通过在序列模型中叠加层来构建深层神经网络。通过在隐藏层之后添加激活函数，我们使网络能够学习数据中更复杂（非线性）的关系。
在这些练习中，你将构建一个有几个隐藏层的神经网络，然后探索ReLU之外的一些激活函数。运行下一个单元格来设置一切！

import tensorflow as tf

# Setup plotting
import matplotlib.pyplot as plt

plt.style.use('seaborn-whitegrid')
# Set Matplotlib defaults
plt.rc('figure', autolayout=True)
plt.rc('axes', labelweight='bold', labelsize='large',
       titleweight='bold', titlesize=18, titlepad=10)

# Setup feedback system
from learntools.core import binder
binder.bind(globals())
from learntools.deep_learning_intro.ex2 import *

在混凝土数据集中，您的任务是预测根据各种配方制造的混凝土的抗压强度。
在不做任何更改的情况下运行下一个代码单元以加载数据集。

import pandas as pd

concrete = pd.read_csv('../input/dl-course-data/concrete.csv')
concrete.head()

1） 输入维度

这项任务的目标是“CompressiveStrength”专栏。剩下的几列是我们将用作输入的功能。
这个数据集的输入维度是什么？

# YOUR CODE HERE
input_shape = ____

# Check your answer
q_1.check()

2） 定义一个线性模型和隐藏层

现在创建一个有三个隐藏层的模型，每个层有512个单元和ReLU激活。确保包含一个单元的输出层且不激活，并将input_shape作为参数输入到第一层。

from tensorflow import keras
from tensorflow.keras import layers

# YOUR CODE HERE
model = ____

# Check your answer
q_2.check()

3） 激活层

让我们来探索一些激活功能。
将激活函数附加到密集层Dense的通常方法是将其作为激活参数定义的一部分。但有时你会想在致密层和激活功能之间再加一层。（我们将在第5课中看到一个关于批处理规范化的示例。）在这种情况下，我们可以在自己的激活层中定义激活，如下所示：
layers.Dense(units=8),
layers.Activation('relu')
这完全等同于普通方式：layers.Dense(units=8, activation='relu')。
重写以下模型，使每个激活都位于其自己的激活层Activation中。

### YOUR CODE HERE: rewrite this to use activation layers
## 重写以下代码，即将一行代码拆分成两行，分别是Dense 和 Activation
model = keras.Sequential([
    layers.Dense(32, activation='relu', input_shape=[8]),
    layers.Dense(32, activation='relu'),
    layers.Dense(1),
])

# Check your answer
q_3.check()

可选：ReLU的替代方案

relu激活有一整套变体——elu、selu和wish，等等——所有这些都可以在Keras中使用。有时，在给定的任务中，一个激活会比另一个更好地执行，因此您可以考虑在开发模型时尝试激活。在大多数问题上，ReLU激活往往表现良好，因此这是一个很好的开始。
让我们看看其中一些的图表。将激活从relu更改为上述其他名称之一。然后运行单元格查看图表。（有关更多想法，请查看文档。）

# YOUR CODE HERE: Change 'relu' to 'elu', 'selu', 'swish'... or something else
activation_layer = layers.Activation('relu')

x = tf.linspace(-3.0, 3.0, 100)
y = activation_layer(x) # once created, a layer is callable just like a function

plt.figure(dpi=100)
plt.plot(x, y)
plt.xlim(-3, 3)
plt.xlabel("Input")
plt.ylabel("Output")
plt.show()

继续前进

现在继续学习第3课，学习如何使用随机梯度下降训练神经网络。

答案

# 1）输入维度
input_shape = [8]
# you could also use a 1-tuple, like input_shape = (8,)
# 说明 concrete.shape 共有(1030,9) 除去“CompressiveStrength”

# 2）定义线性模型
from tensorflow import keras
from tensorflow.keras import layers

model = keras.Sequential([
    layers.Dense(512, activation='relu', input_shape=input_shape),
    layers.Dense(512, activation='relu'),
    layers.Dense(512, activation='relu'),    
    layers.Dense(1),
])

# 3）激活层
model = keras.Sequential([
    layers.Dense(32, input_shape=[8]),
    layers.Activation('relu'),
    layers.Dense(32),
    layers.Activation('relu'),
    layers.Dense(1),
])