【复杂网络】自学笔记整理

一、复杂系统与复杂网络

1.研究目的
复杂网络是研究复杂系统的一种角度和方法，它主要关注系统中个体相互关联的作用。（一种拓扑结构）
2.当今应用
通过分析社交网络之间的关系，确定人们在社会中的社会关系，比如我们用复杂网络分析恐怖分子的多层社会网络，进而得到追踪他们的线索，以此方便警方抓捕。
3.发展背景
（1）计算机技术的飞速发展
（2）网络普适性的发现
（3）理论研究的发展
4.关心问题
（1）如何定量刻画复杂网络？
（2）网络如何实现发展？
（3）网络特定结构的后果是什么？
5.复杂网络的结构及特点
（1）规则网络
一般情况下，集聚系数较大，平均最短路径较长。
（2）随机网络
当p不小时，集聚系数较小，平均最短路径较短。
（3）小世界网络
（4）无标度网络
一般情况下，分成呈幂律分布。
6.顶点重要性度量
（1）度：你有几个朋友 （度是个体指标，分布是整体指标）
（2）集聚系数：你的朋友之间，他们还是不是朋友
（3）介数：整个网络中，通过你的最短路径有多少
（4）接近中心性：你是否位于网络中心
扩展：
（5）谷歌PageRank：通过扩散行为，建立了从全局刻画重要性的指标，它是一个迭代过程
7.顶点度的匹配关系
（1）同向匹配：高度的顶点与高度的顶点相连接（社会网络）
（2）反向匹配：高度的顶点与低度的顶点相连接

二、复杂性思维——北师大教授张江课程

课时一 什么是复杂性思维

1.研究复杂系统的目的：用来做计算机模拟。
2.“时间之箭”和 “因果箭头”
前者表示任何事物的演化都有一个方向性，后者表示有因必有果，有果必有因。
3.区块链
定义：它是一个分布式的存储系统，不需要中心控制者，全部由机器控制管理。
4.技术奇点
定义：它表示机器发展到超越人类认知的时间点。
5.复杂系统
关键点：
（1）系统中个体数有一定的数量级（一般10^2以上）
（2）系统中的个体具有紧密的联系
6.复杂性科学
关键点：
（1）统一性 ：统一的观点看待不同学科
（2）涌现：整体大于部分之和

课时二 系统科学简史与现代复杂系统科学

1.小世界现象
表现：任何地球上的两个人都可以通过最多6个人相互联系起来。
2.无标度现象
表现：任何网络都存在不平等的现象（幂律分布）。
3.PageRank算法
中心思想：实现按从大到小的顺序得到搜索后网站的排序，常用于搜索引擎中。
4.产品空间（Product Space）
具体表现：
（1）附加价值越高的产品会集中在中心位置，附加价值越低的产品会集中在边缘位置。
（2）发展迅速的国家，在映射到产品空间的图后，其位置会随时间从边缘逐渐移动到中心位置。
5.复杂系统中的物理学
定义：复杂系统中的物理学与广义上的物理学不同，它主要使用到的物理学的研究方法。
6.列维飞行
定义：列维飞行是从分布角度上讲，大部分情况在小范围内流动，也有一小部分情况会流动到较远位置的一种运动模式。另外，它也是动物和人的普遍游走规律。
7.系统科学的发展规律：由数据驱动得到一些发现规律。
8.复杂性科学的核心问题：回答什么是生命。

课时三 蜂群思维与涌现

1.自然界中复杂系统：蜂群、蚁群、鸟群、鱼群
①针对蜂群如何确定最短路径这个问题
（1）生物学角度：蚁群根据信息素浓度大小确定最短路径
（2）计算机角度：可以通过计算机模拟方式确定最短路径
②鸟群的飞行规则（没有随机数，但有随机性）
（1）靠近 （2）对齐 （3）避免碰撞
2.群集系统的特点
（1）由许多单元组织而成
（2）每个个体按照简单的规则行事
（3）个体之间具有一定的自治性
（4）单元之间相互连接
（5）没有强制的中心控制
3.如何运用群集思维
（1）建立隐喻
（2）保证交互
（3）激活个体
（4）减少干预

课时四 涌现与关于“马姨”的讨论

1.涌现与斑图
涌现：人的心理和外在的事物发生的某种共振沟通。
斑图（Pattern）：由系统的时空构型形成的整体模式。
2.涌现的分类
（1）强涌现：“我”的存在。
（2）弱涌现：自然界普遍现象的存在。
3.涌现与因果倒置

注：强涌现发生时，因果箭头开始发生颠倒。

课时五 群体模拟与Netlogo

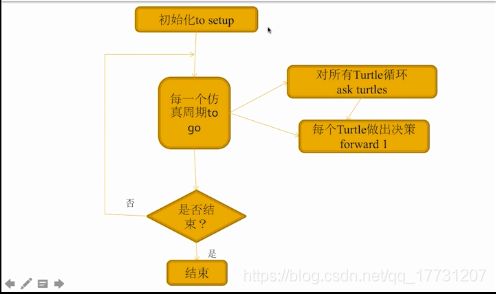
1.计算机模拟：虚拟世界中的空间（数据）与时间（算法、程序）的互动。
2.Netlogo：用来的模拟复杂系统的软件
（1）模拟小球运动
初始化设置：每次点击setup会出现50个随机小球

to setup
   clear-all
   create-turtles 50[
       setxy random-xcor random-ycor
   ]
   set-default-shape turtles "circle"
end

让小球运动起来

to go
   ask turtles[
       forward 1
   ]
end

让小球像虫子一样运动

to go
   ask turtles[
       if random-float 1 < 0.5[
           set heading random 360
       ]
       forward 1
   ]
end

（2）模拟生命游戏
新的对象：Patch
对象属性：patches-own[]
ask patches：对所有的patch对象循环
ask turtles：对所有的turtle对象循环
补：patch对象与turtle对象的不同：前者不需要创建，后者需要创建。
（3）基本思想

课时六 元胞自动机

1.元胞自动机组成
空间：格点
时间：CPU时钟
物理：规则
注：生命游戏（Game of Life）是一个二维的元胞自动机。
2.冯诺依曼贡献
（1）创建了冯诺依曼结构
（2）创立了博弈论
（3）量子计算的奠基人
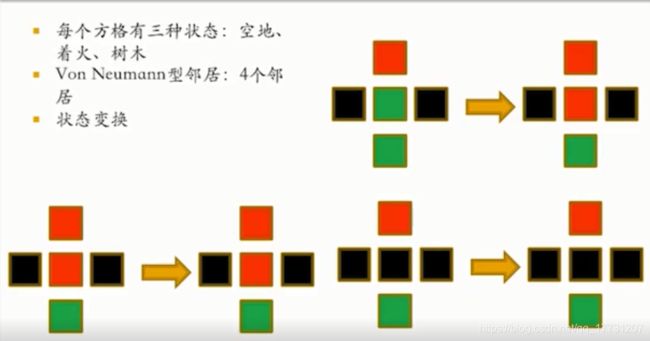
3.二维元胞自动机的邻域
（1）冯诺依曼型领域：上下左右4个邻居
（2）摩尔性邻域：8个邻居
4.火灾模型
特点：遍历所有格点
neighbors：冯诺依曼邻居
numbers：摩尔型邻居
density（森林密度）：density越大，火灾传播速度越快。

5.沙堆模型
特点：二维的元胞自动机；属于冯诺依曼邻居；有五种状态
自组织临界
（1）崩塌会产生级联效应
（2）崩塌的时空呈现幂律分布
（3）系统自发组织进入临界态

课时七 元胞自动机扩展

1.投票模型
特点：随机元胞自动机
结果：最后只有一种观点
2.其他元胞自动机
（1）四角格 （2）三角格 （3）六角格
3.一维元胞自动机（最基础）
特点：每个格子的左右两侧半径为r内的方格为其邻居
基础元胞自动机：r=1,状态为2
可能的规则数：2^8=256
4.一维元胞自动机的运行
按照时间先后顺序上下排列，得到一张二维图

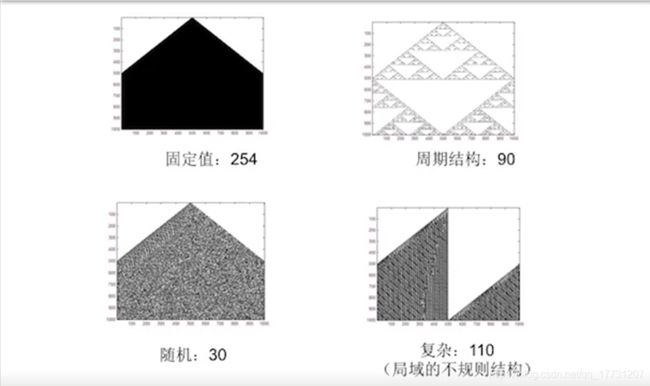
5.一维元胞自动机的应用：奏乐
6.混沌边缘
λ：用来衡量元胞自动机运行后的混沌状态
扩展：
如何得到复杂——让系统运行在混沌的边缘

三、网络科学导论

第一章 引论

1.复杂网络相关应用

随着信息技术的飞速发展，当今社会越来越多的现象会涉及到复杂网络相关应用。
举例：社交网络、搜索引擎

2.Internet的拓扑结构

原因：为预测和提高Internet的性能，特此引入Internet的拓扑结构
具体形式：（1）IP层次 （2）路由器层次 （3）自治系统层次
表现：随时间的推移，IPv4中的IP地址和AS数量逐渐增加

3.WWW

表现：万维网地位的提高以及发展，与搜索引擎的迅速发展密不可分，而搜索引擎属于复杂网络的一个应用领域，因此可见，研究复杂网络有所重要。

4.金融网络和经济网络

背景：经济全球化的大势，给世界上各个国家带来诸多机遇和挑战。提高国际地位的关键，在于成为相对应网络中的关键节点。
表现：在产品空间（Product Space) 相关知识中，我们可以了解到附加价值越高的产品会集中在中心位置，附加价值越低的产品会集中在边缘位置，类比于全球的金融网络和经济网络，我们会发现位于网络中心位置的往往是传播能力强的发达国家。

5.社会网络

背景：六度分离理论的提出
发展：为探究六度分离理论的正确性，科学家们进行了Internet上的小世界实验，进而提出了弱连带和强连带的概念。

6.网络科学的研究目的与研究内容

研究目的：网络科学所要研究的是各种复杂网络之间的共性和处理他们的普适方法。
研究内容：网络科学着眼于复杂网络的定量与定性特征的科学理解。
（1）发现 （2）建模 （3）分析 （4）设计

网络系统的复杂性主要体现在：
（1）结构复杂性
（2）节点复杂性
（3）结构与节点之间的相互影响
（4）网络之间的相互影响（不同领域网络之间相互作用）

第二章 网络与图

1.图的引入

图：用抽象的点和线表示各种实际网络。
图的拓扑性质：主要与网络中结点个数与哪些节点有边直接相连相关。
好处：研究抽象的图，我们可以通过比较不同网络拓扑性质的异同点来建立网络拓扑性质的有效算法。

2.图的类型

（1）加权有向图 （加权和有向指的是边）
（2）加权无向图
（3）无权有向图
（4）无权无向图

3.简单图

类型：没有重边和闭环的无权无向图
假设边数为M，顶点数为N，则无向图中边数与顶点数的关系为：

极端情形：
（1）空图 （2）完全图
假设边数为M，顶点数为N，则有向图中边数与顶点数的关系为：

4.图的计算机表示

（1）邻接矩阵（稠密图）
（2）邻接表（稀疏图）
（3）三元组（加权有向图）

5.共引与文献耦合

共同点：都属于有向网络到无向网络的对偶方法
（1）共引：有向网络中节点i和j的共引数（Cij）定义为同时有出边指向节点i和节点j的节点数。
特殊情况：Cii表示节点i的入度。
转换到无向网络：基于共引矩阵，一个有向网络对应的无向网络定义为：如果Cij>0，那么节点i和j之间就有一个边。
（2）文献耦合：有向网络中节点i和j的文献耦合（Cij）定义为两个节点同时指向其他节点的数量。

结论：共引程度反映的是两篇文章同时被多少篇其他文章引用；文献耦合程度反映的是两篇文章引用了多少篇相同的参考文献。

6.路径与连通性

简单路径：各个顶点都互不相同的路径是简单的。
判断网络是否连通：
（1）当且仅当I+A+A²+…+A^N-1是正矩阵，即所有元素都是正的。
（2）当且仅当邻接矩阵是不可约的。

7.Menger定理（门杰定理）

点形式：所需去除的顶点的最少数目等于连接两个顶点的独立的简单路径的最大数目。->点割集
边形式：所需去除的边的最少数目等于连接两个顶点不相交的简单路径的最大数目。 ->边割集

8.最小生成树

Prim算法：适合计算边稠密的网络的最小生成树。
Kruskal算法：适合计算边稀疏的网络的最小生成树。

9.二分图

定义：图中的每条边的两个节点分别属于顶点集的两个子集中。

二分图的匹配：设G=（X,E,Y）为二分图，F为边集E的一个子集。如果F中任意两条边都没有公共端点，就称F为图G的一个匹配。

第三章 网络基本拓扑性质

1.网络稠密性与稀疏性

网络的密度ρ：
注：M表示网络中的实际边数，分母表示具有N个节点的网络中可能存在的最大边数。
网络稠密：当N趋于无穷时，ρ为非零常数，表示网络是稠密的；
网络稀疏：当N趋于无穷时，ρ为0，表示网络是稀疏的。

2.平均路径长度与直径

节点i与j之间的距离：连接这两个节点的最短路径上的边的数目。
在无向无权图中：
平均路径长度：任意两个节点之间的距离的平均值。
注意：一个含有N个节点和M条边的网络的平均路径长度可以用时间量级为O（MN）的广度优先搜索算法来确定。
直径：网络中任意两个节点之间的距离最大值称为网络的直径。

3.聚类系数（Clustering Coefficient）

（1）无向无权图情形
定义：表示一个节点的邻居之间有边的个数与所有邻居之间都有边个数的比值。

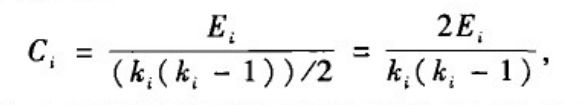
注：其中Ei表示节点的邻居实际存在边的个数，若一个节点有0个或1个邻居节点，那么聚类系数Ci=0。
三元组定义：

一个网络的聚类系数：网络中所有节点聚类系数的平均值。
（2）有向有权图情形

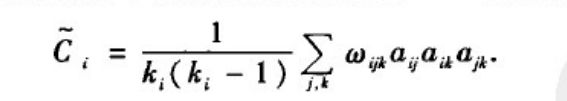
4.度分布与幂律分布

度分布定义：指网络中一个随机选择的节点度为k的概率。
均匀网络：正态分布、泊松分布
长尾分布：幂律分布
幂律分布公式：

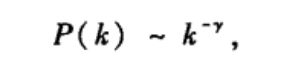
其中γ为幂指数，一般取2-3.
注：幂律网络和无标度网络不能说它们是等价的，一般只有幂指数较小的幂律网络才能说是无标度网络。

第四章 度相关性与社团结构

1.度相关性

定义：又称为网络的二阶度分布特性。
平均度：K = 2M/N
度分布：P(k) = n(k) / N，其中n(k)表示度为k的节点个数，即如果随机选择一个节点i，那么节点的度为k的概率为P（k）。

2.联合概率分布

定义：联合概率P(j,k)定义为网络中随机选取的一条边的两个端点的度分别为j和k的概率,即为网络中度为j的节点和度为k的节点之间存在的边数占网络总边数的比例。
公式：

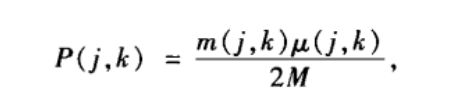
性质：
（1）对称性 （2）归一化 （3）余度分布

第五章 节点重要性与相似性

1.无向网络节点重要性指标

（1）度中心性（Degree Centrality,DC）
定义：一个节点的度越大，意味着该节点在网络中越重要。
公式：度中心值(DC)

（2）介数中心性（Betweenness Centrality,BC）
定义：表示经过该边或该点的最短路径的数量。
公式：边介数/点介数(BC)

（3）接近中心性（Closeness Centrality,CC）
定义：若一个点到其他所有点的平均距离为d,则接近中心性为1/d（d的倒数）。
公式：接近数（CC）

（4）k壳与k核
k壳分解：按度数递增k从0开始，依次去除掉图中度为k的节点，最后剩下的节点即为最重要的节点。
优点：k壳分解相比度中心性的优点在于，可以排除一些度很大但并不是最重要的节点。

（5）特征向量中心性（Eigenvector centrality,EC）
基本思想：一个节点的重要性既取决于其邻居节点的数量，也取决于其邻居节点的重要性。
公式：特征向量中心性

2.HITS算法

基本思想：每个网页的重要性有两个刻画指标——权威性和枢纽性。其中一个网页的权威值由指向这个网页的所有页面的枢纽值确定，而一个网页的枢纽值由该网页指向的所有页面的权威值决定。
枢纽值 ——> 权威值
快速理解：举一个例子，一篇具有创新性的文章被很多人引用，那么这篇文章可以说具有权威性；一篇综述概况总结很多高权威的论点，那么这篇综述可以说具有枢纽性。

3.PageRank算法

基本思想：WWW上一个页面的重要性取决于指向它的其他页面的数量和质量，根据网页PR值的大小确定页面的重要程度。
计算公式：

​其中，Bu是所有链接到网页u的网页集合，网页v是属于集合Bu的一个网页，L(v)则是网页v的对外链接数(即出度).
步骤：
（1）给每个网页一个PR值。
（2）通过（投票）算法不断迭代，直至达到平稳分布为止。
补充：网络中PR值的总和为1。

4.链路预测

（1）链路预测
定义：它是指如何通过已知的各种信息预测给定网络中尚不存在连边的两个节点之间产生连接的可能性。
基本假设：如果两个节点的相似性越大，那么两个节点之间有链接的可能性越大。
应用：朋友推荐
（2）衡量指标

• AUC:测试集中的边的分数值比随机选择的一个不存在的边的分数值高的概率。
  
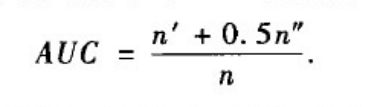
• Precision:只考虑排在前L位的边是否预测准确,即前L个预测边中预测准确的比例。
  

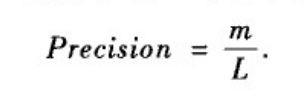
5.节点相似性指标

（1）基于局部信息的相似性指标
典型代表：共同邻居（CN）
（2）基于全局信息的相似性指标
典型代表：局部路径指标（LP）——在共同邻居的基础上，考虑了三阶邻居的影响。
（3）基于随机游走的相似性指标

第六章 随机网络模型

1.全局耦合网络

定义：如果一个网络中的任意两个节点之间都有边直接相连，那么就称该网络为一个全局耦合网络。
局限性：大型实际网络都是稀疏的，边数目最多有O（n）。
聚类系数：1

2.最近邻耦合网络

定义：如果在一个网络中,每一个节点只和它周围的邻居节点相连,那么就称该网络为最近邻耦合网络。
特征：网络的拓扑结构是由节点之间的相对位置决定的,随着节点位置的变化网络拓扑结构可能发生切换。
特点：聚类系数较高，但平均路径长度较大。

3.星形耦合网络

定义：它有一个中心点,其余的N-1个点都只与这个中心点连接，而它们彼此之间不连接。
聚类系数：0

4.ER随机图模型

（1）具有固定边数的ER随机图模型 G（N,M）
定义：N个节点的图中，在任意两个节点之间添加M条边，其中选择的是两个不同的没有边连接的节点对。
（2）具有固定连边概率的ER随机图模型 G（N,p）
定义：把N个节点中任意两个不同的节点之间有一条边的概率固定为p，生成随机数r（0-1之间），若r,则在两个节点之间添加边。
特点：具有较小的平均路径长度，但没有高聚类特性。

第七章 小世界网络模型

1.WS小世界模型

构建方法：在规则网络中添加一些随机性（随机重连），通过调节重连概率p实现WS小世界模型的构建。

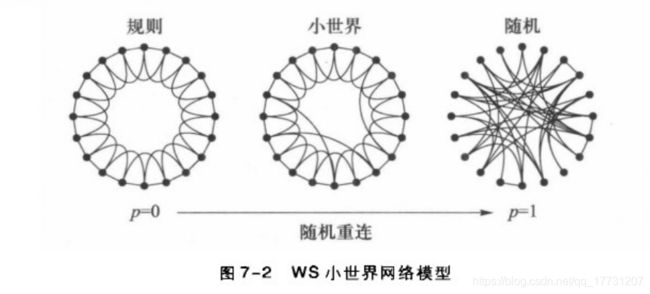
区分WS小世界网络模型与ER随机图模型：
节点的度不同：在WS小世界模型中，每个节点的度至少为K/2，而ER随机图模型任意节点的度没有限制。

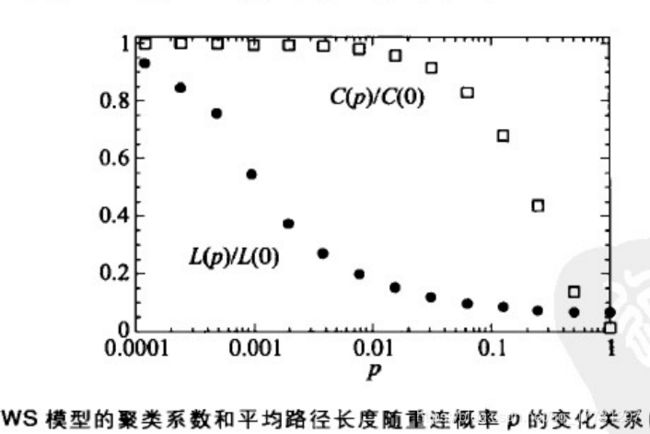
分析结论：当重连概率p较小时，网络的聚类系数较高和平均路径长度较小。

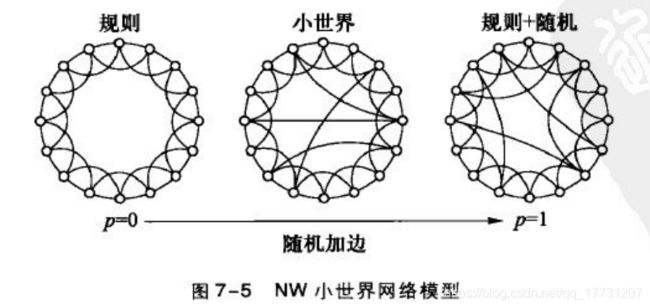
2.NW小世界模型

构建方法：通过用“随机化加边”代替“随机化重连”得到的模型，相当于在最近耦合网络中叠加一个一定边数的随机图，当p较小且N很大时，可近似等价于WS小世界网络模型。

第八章 无标度网络模型

1.鲁棒性

定义：对于给定的网络，如果在移走少量节点后网络中的绝大部分节点是连通的，那么就称该网络的连通性对节点故障具有鲁棒性。

2.随机网络和无标度网络鲁棒性的比较

（1）无标度网络
无标度网络对随机节点故障具有较高的鲁棒性；
无标度网络对蓄意攻击具有高度的脆弱性。
原因： 无标度网络的网络度分布具有极端非均匀性，即绝大多数节点的度较小，只有一小部分节点的度较大。
（2）随机网络
随机网络对随机节点故障具有高度的脆弱性。

既然看到最后了，欢迎点赞收藏一下吧！！