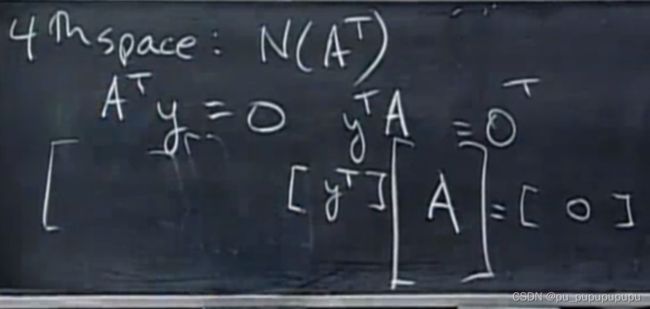线性代数基础6--空间的基,维数,以及四种重要子空间.
1,线性相关与线性无关
背景知识:如果一个矩阵A为m×n的,那么当n>m时,AX=0必然有无穷多解.因为必然存在着自由向量.
线性无关:对于一组向量,如果除了全为0的线性组合,再也找不到一组线性组合,能让向量与这一组线性组合的结果为0,那么就说这一组向量是线性无关的.否则就称,这一组向量线性相关.
这个背景知识告诉我们什么?
三个二维向量必相关,当n>m的情况下,n个m维向量必相关,这是因为
如果n中的m个向量线性无关,那么他就可以表示m维空间中的任意一个向量.这时候再添加n-m个向量,必然可以用m个向量表述出来.所以必相关.
另外一个重要的关系,AX=0只有0解也可以说时r=n,就说明A中向量线性无关,有解就说明线性相关.以及r 2,一些向量生成一个空间 所以单位矩阵的零空间必然只有0. 那么Rn空间中n个向量(隐含条件其实是方阵,因为Rn空间,向量维数必然是n)如果是基的话,那这n个向量一定线性无关,构成的矩阵一定可逆并且列满秩. 3,如果给定一个空间,那么它有无数组基,但是基的个数一定是相同的. 在这里我们知道一个定理,A的秩=A列空间的维数. 另外,需要知道.A的列空间与X的0空间有本质的不同. 4, 5,矩阵的四个基本子空间 对于列空间,我们如何求解它的一组基 对于零空间,它的维数=n-A的秩,它最简单的一组基就是特殊解. 对于行空间,它的维数也为r.并且由于零空间和行空间最大空间都为Rn,所以这两个维数加起来就等于n. 对于左零空间,它的维数为m-r,同理左零空间维数与列空间维数加起来为m. 最左边矩阵就是我们求到的E矩阵. 6,矩阵空间
如前面提到的列空间.也就是这个空间中包含向量的所有线性组合.
我们关心的是:即可以生成指定空间,向量又是线性无关的情况.就是刚刚好生成这个空间的情况.
这样就引出了基的概念.
1,基之间线性无关
2,这些基生成一个空间.

这个例子说明生成一个三维空间,需要三个三维向量.如果只有两个三维向量,得到的是一个平面.如果多一个向量,就线性相关.如果多一行,就成了R4空间中的一个三维子空间.
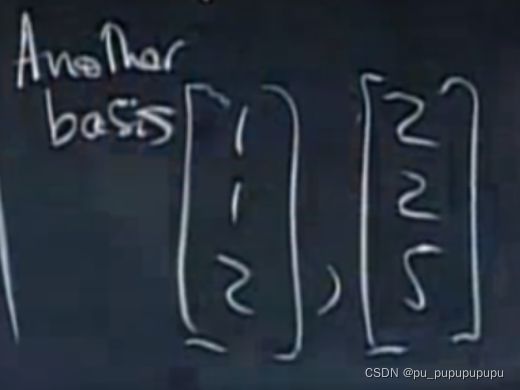
这两个向量是哪一个空间的一组基.是R3中一个平面的一组基
可以说,基的个数决定了空间的大小.例如上例,它的基只有2个,那么它只能表示一个平面.虽然是三维向量,但大小也只能是一个平面.
这样就引出一个概念:空间的维数.
基的个数就是这个空间的维数.注意你可以说,一个空间是二维空间,但他不一定是R2

写出这个列空间的一组基,有无数组,简单的就是一二两列.但是不可以说(1,0,0)和(0,1,0)是一组基,因为生成的平面是不同的.
注意一个矩阵是不可以说维数的.不可以说是A的维数,而是A组成列空间的维数.同样的,矩阵才有秩,不可以说是子空间的秩.
那么这个矩阵的秩=空间的维数,就这样将矩阵与空间联系了起来.
那么这两个之间有什么联系.0空间的维数就等于自由向量的个数.所以一个很重要的结论.n-r(A)=0空间的维数,之前我们用它来算自由向量的个数.

上述三个向量是否为可以构成R3的一组基.答案是不可以,并不需要找到一个线性组合使它等于零,因为这个矩阵第一行第二行相同,所以矩阵一定不可逆.

如果说A为m×n的,
列空间,记为C(A),C(A)在Rm空间中,这里说的是最大空间.
零空间,记为N(A),N(A)在Rn空间中,因为他表示的是自由变量个数.
行空间,记为C(A的转置).这里其实就是A转置的列空间.A所有行向量的线性组合.在空间Rn中
A转置的零空间,记为N(A的转置),这个也可以叫做A的左零空间.在空间Rm中.
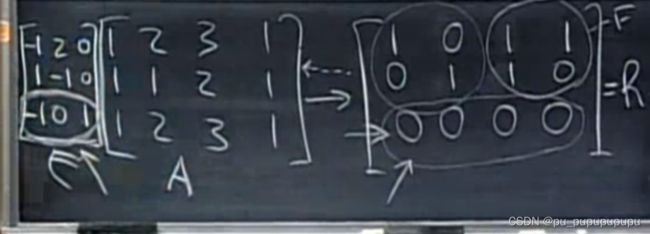
我们得到A的秩,A的秩就等于列空间基的个数,另外,注意在A化为U的过程中进行行变换,但是列空间会变化,行空间则不会变化.所以A的列空间不等于U的列空间.
如图,我们将A化为R,从R中我们可以直接看出行空间的一组基就是前两行,由于在变化过程中,列空间发生变化,所以无法直接得到.
也许会问,为什么行空间在A变为R的过程中保持不变.这是因为进行行变换只是在进行行向量的线性组合.所以产生空间不变.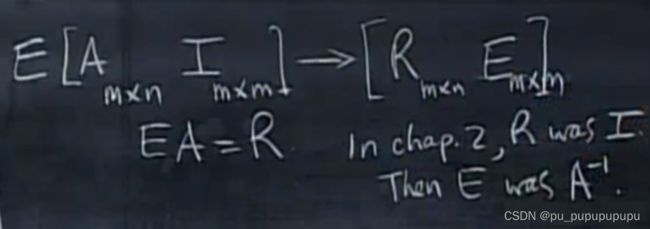
如上图的思想用到了矩阵求逆的思想,但是对于非方阵,无法求逆,我们在A后面添加一个单位矩阵,与A行数相同,那么最后将A化简为R,后面的I就化简为E,这里E中包含了我们所做的初等行变换.
这里跟着I真的可以保留所有的初等行变换吗?毕竟两个矩阵的列数不同
这是可以的,因为在行变换过程中,后面的列并不会单独进行计算.所以只要行保持一致就可以记录.
这里有一个重要的等式EA=R
我们知道左零空间的维数为m-r(A),对于本例来说就是1,所以左零空间就是一条线,那么他的基是什么.从E中最后一行可以看到,A第一行与第三行相减就是0,到此就找到了左零空间的一个基.
这就启示我们,为什么左零空间的维数是m-r(A),因为在R中会有m-r(A)行0,也就是基的所在.所以要求左零空间就要知道E,E就是通过上面方法求出.
将Rn扩展到Rn×n,即其中每个向量都是n×n的矩阵.
在下一讲会详细说明.