机器学习（四）ROC 和 AUC

ROC 和 AUC

AUC是一种模型分类指标，且仅仅是二分类模型的评价指标。AUC是Area Under Curve的简称，那么Curve就是ROC（Receiver Operating Characteristic），翻译为"接受者操作特性曲线"。

ROC

曲线由两个变量TPR和FPR组成，这个组合以FPR对TPR，即是以代价(costs)对收益(benefits)。

• x轴为假阳性率（FPR）：在所有的负样本中，分类器预测错误的比例

  $$FPR=\frac{FP}{FP+TN}$$

• y轴为真阳性率（TPR）：在所有的正样本中，分类器预测正确的比例（等于Recall）

  $$TPR=\frac{TP}{TP+FN}$$

为了更好地理解ROC曲线，我们使用具体的实例来说明：

如在医学诊断中,判断有病的样本。那么尽量把有病的揪出来是主要任务，也就是指标TPR，要越高越好。而把没病的样本误诊为有病的，也就是指标FPR，要越低越好。

不难发现,这两个指标之间是相互制约的。如果某个医生对于有病的症状比较敏感，稍微的小症状都判断为有病,那么他的tpr指标应该会很高，但是fpr指标也就相应地变高。最极端的情况下,他把所有的样本都看做有病,那么tpr达到1,fpr指标也为1。

我们以FPR为横轴,TPR为纵轴,得到如下ROC空间。

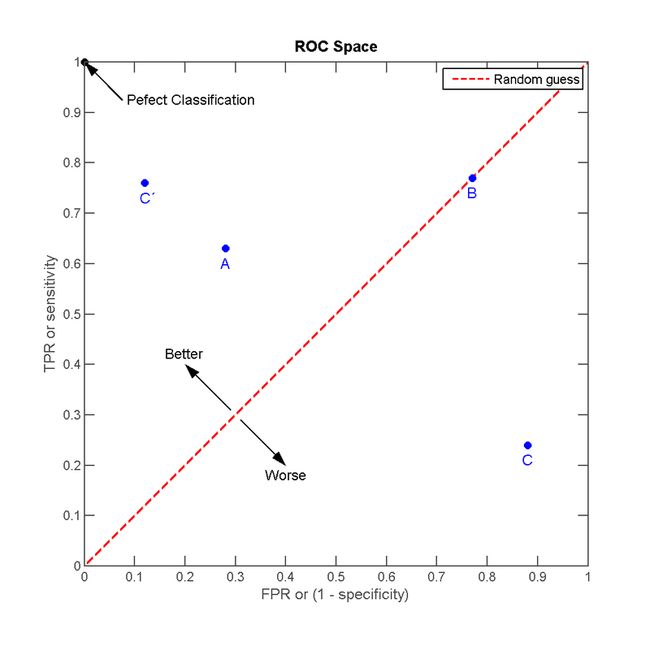
我们可以看出，左上角的点(FPR=0,TPR=1)，为完美分类，也就是这个医生医术高明，诊断全对。点A(TPR>FPR),医生A的判断大体是正确的。中线上的点B(TPR=FPR),也就是医生B全都是蒙的，蒙对一半，蒙错一半；下半平面的点C(TPR

AUC

AUC定义：

AUC值为ROC曲线所覆盖的区域面积，显然，AUC越大，分类器分类效果越好。

AUC的物理意义

AUC的物理意义正样本的预测结果大于负样本的预测结果的概率。所以AUC反应的是分类器对样本的排序能力。

另外值得注意的是，AUC对样本类别是否均衡并不敏感，这也是不均衡样本通常用AUC评价分类器性能的一个原因。

下面从一个小例子解释AUC的含义：小明一家四口，小明5岁，姐姐10岁，爸爸35岁，妈妈33岁建立一个逻辑回归分类器，来预测小明家人为成年人概率，假设分类器已经对小明的家人做过预测，得到每个人为成人的概率。

例子中并不关注小明是不是成人，而关注的是，预测为成人的概率的排序。

**问题①：**以下为三种模型的输出结果，求三种模型的AUC。

	小明	姐姐	妈妈	爸爸
a	0.12	0.35	0.76	0.85
b	0.12	0.35	0.44	0.49
c	0.52	0.65	0.76	0.85

AUC只与概率的相对大小（概率排序）有关，和绝对大小没关系。由于三个模型概率排序的前两位都是未成年人（小明，姐姐），后两位都是成年人（妈妈，爸爸），因此三个模型的AUC都等于1。

AUC只关注正负样本之间的排序，并不关心正样本内部，或者负样本内部的排序。这也体现了AUC的本质：任意个正样本的概率都大于负样本的概率的能力

例子中AUC只需要保证（小明和姐姐）（爸爸和妈妈），小明和姐姐在前2个排序，爸爸和妈妈在后2个排序，而不会考虑小明和姐姐谁在前，或者爸爸和妈妈谁在前。

**问题②：**以下已经对分类器输出概率从小到大进行了排列，哪些情况的AUC等于1， 哪些情况的AUC为0（其中背景色表示True value，红色表示成年人，蓝色表示未成年人）。

D 模型, E模型和F模型的AUC值为1，C模型的AUC值为0

AUC的计算：

• 法1：AUC为ROC曲线下的面积，那我们直接计算面积可得。面积为一个个小的梯形面积（曲线）之和。计算的精度与阈值的精度有关。

• 法2：根据AUC的物理意义，我们计算正样本预测结果大于负样本预测结果的概率。取n1*n0(n1为正样本数，n0为负样本数)个二元组，比较score（预测结果），最后得到AUC。时间复杂度为O(N*M)。

• 法3：我们首先把所有样本按照score排序，依次用rank表示他们，如最大score的样本，rank=n (n=n0+n1，其中n0为负样本个数，n1为正样本个数)，其次为n-1。那么对于正样本中rank最大的样本，rank_max，有n1-1个其他正样本比他score小,那么就有(rank_max-1)-(n1-1)个负样本比他score小。其次为(rank_second-1)-(n1-2)。最后我们得到正样本大于负样本的概率为
  $$AUC=\frac{{\sum }_{正样本}rank(score)-\frac{n_1\ast (n_1+1)}{2}}{n_0\ast n_1}$$

下面说明如何利用ROC曲线下的面积求解AUC。

• 阈值取值的含义：

比如阈值取0.9，即将模型输出概率大于等于0.9的样本预测为正例，将模型输出概率小于0.9的样本预测为负例

• 阈值不同取值与真正例率(TPR)和假正例率(FPR)的关系：

阈值取1，真正例率(正样本预测正确)：0(因为爸爸、妈妈都预测错误了)，假正例率(负样本预测错误)：0(小明和姐姐都没有预测错误)

阈值取0.9，即将大于0.9的概率预测为正例，小于 0.9的概率预测为负例，所以真正例率(正样本预测正确)：50%(爸爸预测正确，妈妈预测错误),假正例率(负样本预测错误)：0

阈值取0.75，真正例率：50%(爸爸预测正确，妈妈预测错误),假正例率：50%(小明预测正确，姐姐预测错误)

阈值取0.36，真正例率：1(爸爸、妈妈都预测正确)，假正例率：50%(小明预测正确，姐姐预测错误)

阈值取0.18，真正例率：1(爸爸、妈妈都预测正确)，假正例率：1(小明和姐姐都预测错误)

阈值取0，真正例率：1(爸爸、妈妈都预测正确)，假正例率：1(小明和姐姐都预测错误)

经过观察，发现ROC曲线下的面积AUC值为0.5；

下面有一个简单的例子说明如何利用方法三求解AUC：

• 真实标签为 (1, 0, 0, 1, 0)

• 预测结果1（0.9, 0.3, 0.2, 0.7, 0.5）

• 预测结果2（0.9, 0.3, 0.2, 0.7, 0.8）)

• 分别对两个预测结果进行排序，并提取他们的序号

  • 结果1 (5, 2, 1, 4, 3)
  • 结果2 (5, 2, 1, 3, 4)

• 对正分类序号累加

  • 结果1：${\sum }_{正样本}RANK(score)=5+4=9$
  • 结果2: ${\sum }_{正样本}RANK(score)=5+3=8$

• 计算两个结果的AUC:

  • 结果1：$AUC=\frac{9-\frac{2\ast (2+1)}{2}}{2\ast 3}=1$
  • 结果2：$AUC=\frac{8-\frac{2\ast (2+1)}{2}}{2\ast 3}=0.833$