python深度学习之残差网络ResNets

1、什么是ResNets

我们知道，如果神经网络层数越多，网络越深，源于梯度消失和梯度爆炸的影响，整个模型难以训练成功。解决的方法之一是人为地让神经网络某些层跳过下一层神经元的连接，隔层相连，弱化每层之间的强联系。这种神经网络被称为Residual Networks(ResNets)。

Residual Networks由许多隔层相连的神经元子模块组成，我们称之为Residual block。单个Residual block的结构如下图所示：

$$\begin{gathered} z^{[l+1]}=W^{[l+1]}{a}^{[l]}+b^{[l+1]} \\ a[l+1]=g(z[l+1]) \\ {z}^{[l+2]}=W^{[l+2]}{a}^{[l+1]}+b^{[l+2]} \\ {a}^{[l+2]}=g(z^{[l+2]}+a^{[l]}) \end{gathered}$$
a^[l]直接直接隔层与下一层的线性输出相连，与z^[l+2]共同通过激活函数（ReLU）输出a^[l+2]。

该模型由Kaiming He, Xiangyu Zhang, Shaoqing Ren和Jian Sun共同提出。由多个Residual block组成的神经网络就是Residual Network。实验表明，这种模型结构对于训练非常深的神经网络，效果很好。另外，为了便于区分，我们把非Residual Networks称为Plain Network。

可以看出，即使发生了梯度消失，W^[l+2]≈0 , b^[l+2]≈0，也能直接建立a^[l+2]与a^[l]的线性关系，且a^[l+2]=a^[l]，这其实就是identity function。a^[l]直接连到a^[l+2]，从效果来说，相当于直接忽略了a^[l]之后的这两层神经层。这样，看似很深的神经网络，其实由于许多Residual blocks的存在，弱化削减了某些神经层之间的联系，实现隔层线性传递，而不是一味追求非线性关系，模型本身也就能“容忍”更深层的神经网络了。而且从性能上来说，这两层额外的Residual blocks也不会降低Big NN的性能。

有一点需要注意的是，如果Residual blocks中a^[l]和a^[l+2]的维度不同，通常可以引入矩阵W_s，与a^[l]相乘，使得W_s∗a^[l]的维度与a^[l+2]一致。参数矩阵W_s有来两种方法得到：一种是将W_s作为学习参数，通过模型训练得到；另一种是固定W_s值（类似单位矩阵），不需要训练，W_s与a^[l]的乘积仅仅使得a^[l]截断或者补零。这两种方法都可行。

2、构建一个ResNet（50层）

ResNet中的模块由两种模块组成，分别是identity block和convolutional block

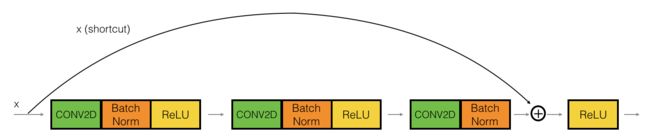
2.1 identity block

在第一层和第三层的CONV2D层我们采用1x1卷积操作,效果等同于Plain Network中a^[l]到a^[l+1]的过程类似于神经网络的全连接层,优点是可以用来缩减输入图片的通道数目。

第二层的CONV2D层采用(f, f)卷积,填充类型是same。注意在第三层"X = Activation(‘relu’)(X)“之前需要增加"X = Add()([X,X_shortcut])”

# UNQ_C1
# GRADED FUNCTION: identity_block

def identity_block(X, f, filters, training=True, initializer=random_uniform):
    """
    Implementation of the identity block as defined in Figure 4
    
    Arguments:
    X -- input tensor of shape (m, n_H_prev, n_W_prev, n_C_prev)
    f -- integer, specifying the shape of the middle CONV's window for the main path
    filters -- python list of integers, defining the number of filters in the CONV layers of the main path
    training -- True: Behave in training mode
                False: Behave in inference mode
    initializer -- to set up the initial weights of a layer. Equals to random uniform initializer
    
    Returns:
    X -- output of the identity block, tensor of shape (n_H, n_W, n_C)
    """
    
    # Retrieve Filters
    F1, F2, F3 = filters
    
    # Save the input value. You'll need this later to add back to the main path. 
    X_shortcut = X
    
    # First component of main path
    X = Conv2D(filters = F1, kernel_size = 1, strides = (1,1), padding = 'valid', kernel_initializer = initializer(seed=0))(X)
    X = BatchNormalization(axis = 3)(X, training = training) # Default axis
    X = Activation('relu')(X)
    
    ### START CODE HERE
    ## Second component of main path (≈3 lines)
    X = Conv2D(filters = F2, kernel_size = f, strides = (1, 1), padding = 'same', kernel_initializer= initializer(seed = 0))(X)
    X = BatchNormalization(axis = 3)(X, training = training)
    X = Activation('relu')(X) 

    ## Third component of main path (≈2 lines)
    X = Conv2D(filters = F3, kernel_size = 1, strides = (1, 1), padding = 'valid', kernel_initializer = initializer(seed = 0))(X)
    X = BatchNormalization(axis = 3)(X, training = training)
    
    ## Final step: Add shortcut value to main path, and pass it through a RELU activation (≈2 lines)
    X = Add()([X,X_shortcut])
    X = Activation('relu')(X)
    ### END CODE HERE

    return X

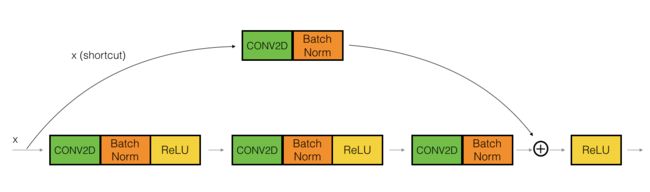
2.2 convolutional block

ResNet中的"convolutional block"是第二种块类型。当输入和输出维度不匹配时，可以使用这种类型的块。与identity block的不同之处在于，convolutional block的shortcut路径中存在一个 CONV2D 层，用于将输入x调整为另一个维度的大小，以便维度与最终需要添加到shortcut主路径所用的维度匹配（这与讲座中讨论的矩阵W_s起到类似的作用）

第一个CONV2D具有形状为（1,1）和步幅为（s，s）的F1个滤波器。其填充为"valid"

第二个CONV2D具有（f，f）的F2滤波器和（1,1）的步幅。其填充为"same"

第三个CONV2D的F3滤波器为（1,1），步幅为（1,1）。其填充为"valid"

Shortcut path：CONV2D具有形状为（1,1）和步幅为（s，s）的F3个滤波器。其填充为"valid"

最后一步将Shortcut路径和主路径添加在一起，然后应用ReLU激活函数。

# UNQ_C2
# GRADED FUNCTION: convolutional_block

def convolutional_block(X, f, filters, s = 2, training=True, initializer=glorot_uniform):
    """
    Implementation of the convolutional block as defined in Figure 4
    
    Arguments:
    X -- input tensor of shape (m, n_H_prev, n_W_prev, n_C_prev)
    f -- integer, specifying the shape of the middle CONV's window for the main path
    filters -- python list of integers, defining the number of filters in the CONV layers of the main path
    s -- Integer, specifying the stride to be used
    training -- True: Behave in training mode
                False: Behave in inference mode
    initializer -- to set up the initial weights of a layer. Equals to Glorot uniform initializer, 
                   also called Xavier uniform initializer.
    
    Returns:
    X -- output of the convolutional block, tensor of shape (n_H, n_W, n_C)
    """
    
    # Retrieve Filters
    F1, F2, F3 = filters
    
    # Save the input value
    X_shortcut = X


    ##### MAIN PATH #####
    
    # First component of main path glorot_uniform(seed=0)
    X = Conv2D(filters = F1, kernel_size = 1, strides = (s, s), padding='valid', kernel_initializer = initializer(seed=0))(X)
    X = BatchNormalization(axis = 3)(X, training=training)
    X = Activation('relu')(X)

    ### START CODE HERE
    
    ## Second component of main path (≈3 lines)
    X = Conv2D(filters = F2, kernel_size = f, strides = 1, padding='same', kernel_initializer = glorot_uniform(seed=0))(X)
    X = BatchNormalization(axis = 3)(X, training=training)
    X = Activation('relu')(X)

    ## Third component of main path (≈2 lines)
    X = Conv2D(filters = F3, kernel_size = 1, strides = 1, padding='valid', kernel_initializer = glorot_uniform(seed=0))(X)
    X = BatchNormalization(axis = 3)(X, training=training)
    
    ##### SHORTCUT PATH ##### (≈2 lines)
    X_shortcut = Conv2D(filters = F3, kernel_size = 1, strides = s, padding='valid', kernel_initializer = glorot_uniform(seed=0))(X_shortcut)
    X_shortcut = BatchNormalization(axis = 3)(X_shortcut, training=training)
    
    ### END CODE HERE

    # Final step: Add shortcut value to main path (Use this order [X, X_shortcut]), and pass it through a RELU activation
    X = Add()([X, X_shortcut])
    X = Activation('relu')(X)
    
    return X

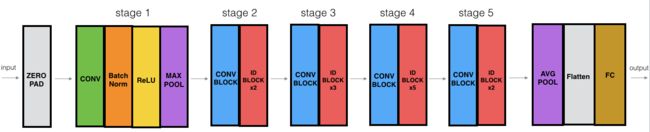
2.3 利用两种模块构建ResNet（50层）

您现在拥有了构建非常深的ResNet所需的块。下图详细描述了此神经网络的体系结构。图中的"ID 块"代表"标识块"，而"ID 块 x3"表示应将 3 个标识块堆叠在一起。

此 ResNet-50 模型的详细信息如下：

• 零填充填充填充输入，padding=(3，3)
• 第 1 阶段：
  • 2D 卷积有 64 个形状滤光片 （7，7），并使用步幅 （2，2）。
  • BatchNorm 应用于输入的"通道"轴。
  • 最大池使用 （3，3） 窗口和 （2，2） 步幅。
• 第 2 阶段：
  • 卷积块使用三组大小为 [64，64，256] 的滤波器，“f” 为 3，“s” 为 1。
  • 2 个标识块使用三组大小为 [64，64，256] 的筛选器，"f"为 3。
• 第 3 阶段：
  • 卷积块使用三组大小为 [128，128，512] 的滤波器，“f” 为 3，“s” 为 2。
  • 3 个标识块使用三组大小为 [128，128，512] 的筛选器，"f"为 3。
• 第 4 阶段：
  • 卷积块使用三组大小为 [256， 256， 1024] 的滤波器，“f” 为 3，“s” 为 2。
  • 5 个标识块使用三组大小为 [256， 256， 1024] 的过滤器，"f"为 3。
• 第 5 阶段：
  • 卷积块使用三组大小为 [512， 512， 2048] 的滤波器，“f” 为 3，“s” 为 2。
  • 2 个标识块使用三组大小为 [512， 512， 2048] 的过滤器，"f"为 3。
• 2D 平均池化使用窗口形状 （2，2）。
• "展平"图层没有任何超参数。
• "全连接（密集）"层使用 softmax 激活将其输入减少到类数。
• 最后用Model函数生成模型

# UNQ_C3
# GRADED FUNCTION: ResNet50

def ResNet50(input_shape = (64, 64, 3), classes = 6):
    """
    Stage-wise implementation of the architecture of the popular ResNet50:
    CONV2D -> BATCHNORM -> RELU -> MAXPOOL -> CONVBLOCK -> IDBLOCK*2 -> CONVBLOCK -> IDBLOCK*3
    -> CONVBLOCK -> IDBLOCK*5 -> CONVBLOCK -> IDBLOCK*2 -> AVGPOOL -> FLATTEN -> DENSE 

    Arguments:
    input_shape -- shape of the images of the dataset
    classes -- integer, number of classes

    Returns:
    model -- a Model() instance in Keras
    """
    
    # Define the input as a tensor with shape input_shape
    X_input = Input(input_shape)

    # Zero-Padding
    X = ZeroPadding2D((3, 3))(X_input)
    
    # Stage 1
    X = Conv2D(64, (7, 7), strides = (2, 2), kernel_initializer = glorot_uniform(seed=0))(X)
    X = BatchNormalization(axis = 3)(X)
    X = Activation('relu')(X)
    X = MaxPooling2D((3, 3), strides=(2, 2))(X)

    # Stage 2
    X = convolutional_block(X, f = 3, filters = [64, 64, 256], s = 1)
    X = identity_block(X, 3, [64, 64, 256])
    X = identity_block(X, 3, [64, 64, 256])

    ### START CODE HERE
    
    ## Stage 3 (≈4 lines)
    X = convolutional_block(X, f = 3, filters = [128,128,512], s = 2)
    X = identity_block(X, 3, [128,128,512])
    X = identity_block(X, 3, [128,128,512])
    X = identity_block(X, 3, [128,128,512])
    
    ## Stage 4 (≈6 lines)
    X = convolutional_block(X, f = 3, filters = [256, 256, 1024], s = 2)
    X = identity_block(X, 3, [256, 256, 1024])
    X = identity_block(X, 3, [256, 256, 1024])
    X = identity_block(X, 3, [256, 256, 1024])
    X = identity_block(X, 3, [256, 256, 1024])
    X = identity_block(X, 3, [256, 256, 1024])

    ## Stage 5 (≈3 lines)
    X = convolutional_block(X, f = 3, filters = [512, 512, 2048], s = 2)
    X = identity_block(X, 3, [512, 512, 2048])
    X = identity_block(X, 3, [512, 512, 2048])

    ## AVGPOOL (≈1 line). Use "X = AveragePooling2D(...)(X)"
    X = AveragePooling2D(2) (X)
    
    ### END CODE HERE

    # output layer
    X = Flatten()(X)
    X = Dense(classes, activation='softmax', kernel_initializer = glorot_uniform(seed=0))(X)
    
    # Create model
    model = Model(inputs = X_input, outputs = X)

    return model

2.4 再次查看ResNet结构

可以采用model.summary查看

model = ResNet50(input_shape = (64, 64, 3), classes = 6)
print(model.summary())

输出结果

Total params: 23,600,006
Trainable params: 23,546,886
Non-trainable params: 53,120

2.5 编译运行模型

model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

3、ResNet的应用实例——识别和分类手势

手势数据集，采用onehot编码

处理数据后，利用模型进行拟合

model.fit(X_train, Y_train, epochs = 10, batch_size = 32)

模型在训练集上的表现如下所示

Epoch 1/10
34/34 [==============================] - 45s 1s/step - loss: 2.5626 - accuracy: 0.4324
Epoch 2/10
34/34 [==============================] - 40s 1s/step - loss: 1.1139 - accuracy: 0.7065
Epoch 3/10
34/34 [==============================] - 38s 1s/step - loss: 0.5291 - accuracy: 0.8389
Epoch 4/10
34/34 [==============================] - 40s 1s/step - loss: 0.5296 - accuracy: 0.8630
Epoch 5/10
34/34 [==============================] - 39s 1s/step - loss: 0.3451 - accuracy: 0.8880
Epoch 6/10
34/34 [==============================] - 39s 1s/step - loss: 0.1698 - accuracy: 0.9361
Epoch 7/10
34/34 [==============================] - 38s 1s/step - loss: 0.0887 - accuracy: 0.9731
Epoch 8/10
34/34 [==============================] - 39s 1s/step - loss: 0.2057 - accuracy: 0.9176
Epoch 9/10
34/34 [==============================] - 39s 1s/step - loss: 0.5623 - accuracy: 0.8880
Epoch 10/10
34/34 [==============================] - 39s 1s/step - loss: 0.3176 - accuracy: 0.9167

preds = model.evaluate(X_test, Y_test)
print ("Loss = " + str(preds[0]))
print ("Test Accuracy = " + str(preds[1]))

模型在测试集的表现

4/4 [==============================] - 2s 184ms/step - loss: 0.3241 - accuracy: 0.8917
Loss = 0.32407525181770325
Test Accuracy = 0.8916666507720947

加载吴恩达团队训练好的一个模型

pre_trained_model = tf.keras.models.load_model('resnet50.h5')

preds = pre_trained_model.evaluate(X_test, Y_test)
print ("Loss = " + str(preds[0]))
print ("Test Accuracy = " + str(preds[1]))

准确率还是蛮高的

4/4 [==============================] - 1s 163ms/step - loss: 0.1596 - accuracy: 0.9500
Loss = 0.15958665311336517
Test Accuracy = 0.949999988079071

reference

deeplearning.ai by Andrew Ng on Couresa

https://blog.csdn.net/red_stone1/article/details/78769236