数据挖掘（一）频繁模式挖掘算法的实现和对比

注：参考多篇CSDN文章所得

一、实验内容

巩固频繁模式挖掘的基本算法原理及特点，设计程序，基于不同特征的数据集比较不同方法的优缺点，并基于算法原理和特点分析造成这种现象的原因。

二、算法原理

1 Apriori

对于Apriori算法，通过限制候选产生发现频繁项集，使用支持度来作为判断频繁项集的标准。Apriori算法的目标是找到最大的K项频繁集。这里有两层意思，首先，我们要找到符合支持度标准的频繁集。但是这样的频繁集可能有很多。第二层意思就是我们要找到最大个数的频繁集。比如我们找到符合支持度的频繁集AB和ABE，那么我们会抛弃AB，只保留ABE，因为AB是2项频繁集，而ABE是3项频繁集。

Apriori算法采用了迭代的方法，先搜索出候选1项集及对应的支持度，剪枝去掉低于支持度的1项集，得到频繁1项集。然后对剩下的频繁1项集进行连接，得到候选的频繁2项集，筛选去掉低于支持度的候选频繁2项集，得到真正的频繁二项集，以此类推，迭代下去，直到无法找到频繁k+1项集为止，对应的频繁k项集的集合即为算法的输出结果。

2.FP-growth

FP-growth算法是基于Apriori原理的，通过将数据集存储在FP（Frequent Pattern)树上发现频繁项集，但不能发现数据之间的关联规则。FP-growth是一种以自底向上方式探索树，由FP树产生频繁项集的算法，通过模式增长挖掘频繁模式。给定上面构建的FP树，算法首先查找以e结尾的频繁项集，接下来是b,c,d，最后是a，由于每一个事务都映射到FP树中的一条路径，因为通过仅考察包含特定节点（例如e）的路径，就可以发现以e结尾的频繁项集，使用与节点e相关联的指针，可以快速访问这些路径。

算法发现频繁项集的过程是：(1)构建FP树；(2)从FP树中挖掘频繁项集。

FPGrowth算法的主要思想：1. 构造频繁1项集：遍历初始数据集构造频繁1项集，并作为项头表，建立将指向fpTree节点对应元素的引用 2. 构造FPTree：再次遍历初始数据集，对于每一条事务中的元素，根据频繁1项集中元素的顺序排序， 由此建立FPTree，记录每条事务的节点在同一条路径上出再的节点次数;  3. 逆序遍历在步骤1中构造的项头表，根据其提供的引用指针，找出fpTree中由该节点到根节点的路径， 即生成每个频繁元素的条件模式基 4.根据每个频繁元素对应的条件模式基，生成其对应的条件fpTree，并删除树中节点记数不满足给定的最小支持度的节点  5.对于每一颗条件fpTree，生成所有的从根节点到叶子节点的路径，由路径中的集合生成其所有非空子集 ，所有这些非空子集和每一个频繁1项集中的元素共同构成了原始数据集中的频繁集。

3.Eclat

Eclat算法使用垂直格式挖掘频繁项集。其过程为：（1）通过扫描一次数据集，把水平格式的数据转换成垂直格式；（2）项集的支持度计数简单地等于项集的TID集的长度；（3）从k=1开始，可以根据先验性质，使用频繁k项集来构造候选（k+1）项集；（4）通过取频繁k项集的TID集的交，计算对应的（k+1）项集的TID集。（5）重复该过程，每次k增加1，直到不能再找到频繁项集或候选项集。Eclat算法加入了倒排的思想，具体就是将事务数据中的项作为key，每个项对应的事务ID作为value。只需对数据进行一次扫描，算法的运行效率会很高。

主要步骤：将数据倒排{ item：TID_set }，然后通过求频繁k项集的交集来获取k+1项集。特点：仅需要一次扫描数据库，TID集合很长的话需要消耗大量的内存和计算时间。

4.不同算法的特点

Apriori算法：需要多次扫描数据库，对于大规模数据效率很低。

FPGrowth算法：两次扫描数据库，采用分治的策略有效降低了搜索开销。

Eclat算法：仅需要一次扫描数据库，如果TID集合很长，需要消耗大量的内存和计算时间。

三、算法代码实现

1.Apriori

def init_c1(data_set_dict, min_support):
    c1 = []
    freq_dic = {}
    for trans in data_set_dict:
        for item in trans:
            freq_dic[item] = freq_dic.get(item, 0) + data_set_dict[trans]
    # 优化初始的集合，使不满足最小支持度的直接排除
    c1 = [[k] for (k, v) in freq_dic.iteritems() if v >= min_support]
    c1.sort()
    return map(frozenset, c1)

def scan_data(data_set, ck, min_support, freq_items):
    """
    计算Ck中的项在数据集合中的支持度，剪枝过程
    :param data_set:
    :param ck:
    :param min_support: 最小支持度
    :param freq_items: 存储满足支持度的频繁项集
    :return:
    """
    ss_cnt = {}
    # 每次遍历全体数据集
    for trans in data_set:
        for item in ck:
            # 对每一个候选项集， 检查是否是 term中的一部分（子集），即候选项能否得到支持
            if item.issubset(trans):
                ss_cnt[item] = ss_cnt.get(item, 0) + 1
    ret_list = []
    for key in ss_cnt:
        support = ss_cnt[key]  # 每个项的支持度
        if support >= min_support:
            ret_list.insert(0, key)  # 将满足最小支持度的项存入集合
            freq_items[key] = support  #
    return ret_list


def apriori_gen(lk, k):
    """
    由Lk的频繁项集生成新的候选项集  连接过程
    :param lk:  频繁项集集合
    :param k:  k 表示集合中所含的元素个数
    :return: 候选项集集合
    """
    ret_list = []
    for i in range(len(lk)):
        for j in range(i+1, len(lk)):
            l1 = list(lk[i])[:k-2]
            l2 = list(lk[j])[:k-2]
            l1.sort()
            l2.sort()
            if l1 == l2:
                ret_list.append(lk[i] | lk[j])  # 求并集
    # retList.sort()
    return ret_list

def apriori_zc(data_set, data_set_dict, min_support=5):
    """
    Apriori算法过程
    :param data_set: 数据集
    :param min_support: 最小支持度，默认值 0.5
    :return:
    """
    c1 = init_c1(data_set_dict, min_support)
    data = map(set, data_set)  # 将dataSet集合化，以满足scanD的格式要求
    freq_items = {}
    l1 = scan_data(data, c1, min_support, freq_items)  # 构建初始的频繁项集
    l = [l1]
    # 最初的L1中的每个项集含有一个元素，新生成的项集应该含有2个元素，所以 k=2
    k = 2
    while len(l[k - 2]) > 0:
        ck = apriori_gen(l[k - 2], k)
        lk = scan_data(data, ck, min_support, freq_items)
        l.append(lk)
        k += 1  # 新生成的项集中的元素个数应不断增加
    return freq_items

2.FP-growth

def create_tree(data_set, min_support=1):
    """
    创建FP树
    :param data_set: 数据集
    :param min_support: 最小支持度
    :return:
    """
    freq_items = {}  # 频繁项集
    for trans in data_set:  # 第一次遍历数据集
        for item in trans:
            freq_items[item] = freq_items.get(item, 0) + data_set[trans]

    header_table = {k: v for (k, v) in freq_items.iteritems() if v >= min_support}  # 创建头指针表
    # for key in header_table:
    #     print key, header_table[key]

    # 无频繁项集
    if len(header_table) == 0:
        return None, None
    for k in header_table:
        header_table[k] = [header_table[k], None]  # 添加头指针表指向树中的数据
    # 创建树过程
    ret_tree = treeNode('Null Set', 1, None)  # 根节点

    # 第二次遍历数据集
    for trans, count in data_set.items():
        local_data = {}
        for item in trans:
            if header_table.get(item, 0):
                local_data[item] = header_table[item][0]
        if len(local_data) > 0:
            ##############################################################################################
            # 这里修改机器学习实战中的排序代码：
            ordered_items = [v[0] for v in sorted(local_data.items(), key=lambda kv: (-kv[1], kv[0]))]
            ##############################################################################################
            update_tree(ordered_items, ret_tree, header_table, count)  # populate tree with ordered freq itemset
    return ret_tree, header_table

def update_tree(items, in_tree, header_table, count):
    '''
    :param items: 元素项
    :param in_tree: 检查当前节点
    :param header_table:
    :param count:
    :return:
    '''
    if items[0] in in_tree.children:  # check if ordered_items[0] in ret_tree.children
        in_tree.children[items[0]].increase(count)  # incrament count
    else:  # add items[0] to in_tree.children
        in_tree.children[items[0]] = treeNode(items[0], count, in_tree)
        if header_table[items[0]][1] is None:  # update header table
            header_table[items[0]][1] = in_tree.children[items[0]]
        else:
            update_header(header_table[items[0]][1], in_tree.children[items[0]])
    if len(items) > 1:  # call update_tree() with remaining ordered items
        update_tree(items[1::], in_tree.children[items[0]], header_table, count)

def update_header(node_test, target_node):
    '''
    :param node_test:
    :param target_node:
    :return:
    '''
    while node_test.node_link is not None:  # Do not use recursion to traverse a linked list!
        node_test = node_test.node_link
    node_test.node_link = target_node

def ascend_tree(leaf_node, pre_fix_path):
    '''
    遍历父节点，找到路径
    :param leaf_node:
    :param pre_fix_path:
    :return:
    '''
    if leaf_node.parent is not None:
        pre_fix_path.append(leaf_node.name)
        ascend_tree(leaf_node.parent, pre_fix_path)

def find_pre_fix_path(base_pat, tree_node):
    '''
    创建前缀路径
    :param base_pat: 频繁项
    :param treeNode: FP树中对应的第一个节点
    :return:
    '''
    # 条件模式基
    cond_pats = {}
    while tree_node is not None:
        pre_fix_path = []
        ascend_tree(tree_node, pre_fix_path)
        if len(pre_fix_path) > 1:
            cond_pats[frozenset(pre_fix_path[1:])] = tree_node.count
        tree_node = tree_node.node_link
    return cond_pats

def mine_tree(in_tree, header_table, min_support, pre_fix, freq_items):
    '''
    挖掘频繁项集
    :param in_tree:
    :param header_table:
    :param min_support:
    :param pre_fix:
    :param freq_items:
    :return:
    '''
    # 从小到大排列table中的元素，为遍历寻找频繁集合使用
    bigL = [v[0] for v in sorted(header_table.items(), key=lambda p: p[1])]  # (sort header table)
    for base_pat in bigL:  # start from bottom of header table
        new_freq_set = pre_fix.copy()
        new_freq_set.add(base_pat)
        # print 'finalFrequent Item: ',new_freq_set    #append to set
        if len(new_freq_set) > 0:
            freq_items[frozenset(new_freq_set)] = header_table[base_pat][0]
        cond_patt_bases = find_pre_fix_path(base_pat, header_table[base_pat][1])
        my_cond_tree, my_head = create_tree(cond_patt_bases, min_support)
        # print 'head from conditional tree: ', my_head
        if my_head is not None:  # 3. mine cond. FP-tree
            # print 'conditional tree for: ',new_freq_set
            # my_cond_tree.disp(1)
            mine_tree(my_cond_tree, my_head, min_support, new_freq_set, freq_items)


def fp_growth(data_set, min_support=1):
    my_fp_tree, my_header_tab = create_tree(data_set, min_support)
    # my_fp_tree.disp()
    freq_items = {}
    mine_tree(my_fp_tree, my_header_tab, min_support, set([]), freq_items)
    return freq_items

3.​​​​​Eclat

import sys
import time
type = sys.getfilesystemencoding()


def eclat(prefix, items, min_support, freq_items):
    while items:
        # 初始遍历单个的元素是否是频繁
        key, item = items.pop()
        key_support = len(item)
        if key_support >= min_support:
            # print frozenset(sorted(prefix+[key]))
            freq_items[frozenset(sorted(prefix+[key]))] = key_support
            suffix = []  # 存储当前长度的项集
            for other_key, other_item in items:
                new_item = item & other_item  # 求和其他集合求交集
                if len(new_item) >= min_support:
                    suffix.append((other_key, new_item))
            eclat(prefix+[key], sorted(suffix, key=lambda item: len(item[1]), reverse=True), min_support, freq_items)
    return freq_items


def eclat_zc(data_set, min_support=1):
    """
    Eclat方法
    :param data_set:
    :param min_support:
    :return:
    """
    # 将数据倒排
    data = {}
    trans_num = 0
    for trans in data_set:
        trans_num += 1
        for item in trans:
            if item not in data:
                data[item] = set()
            data[item].add(trans_num)
    freq_items = {}
    freq_items = eclat([], sorted(data.items(), key=lambda item: len(item[1]), reverse=True), min_support, freq_items)
    return freq_items

四、不同规模、最小支持度以及方法对结果的影响及适用性

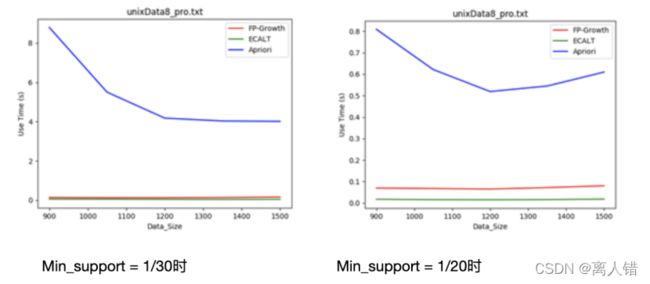
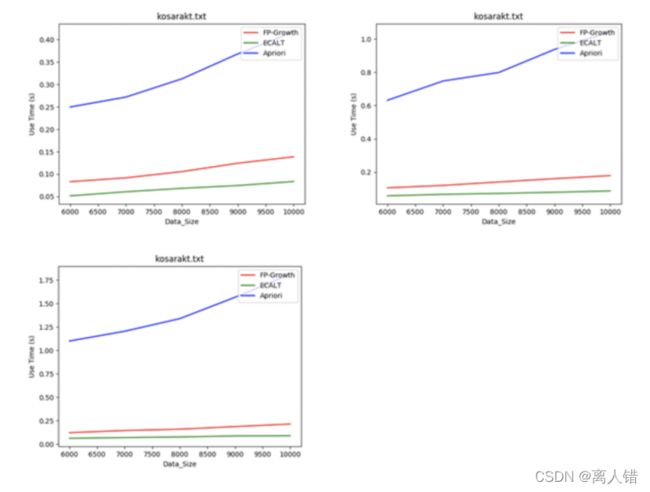
1.不同规模大小数据对各方法结果影响

1）数据集：unxiData8     规模：900-1500

 

2）数据集：kosarakt    规模：6000-10000

 

结论：一般情况下，数据规模越大，Apriori算法效率越低。因为该算法需要多次扫描数据库，数据量越大，扫描数据库带来的消耗越多。

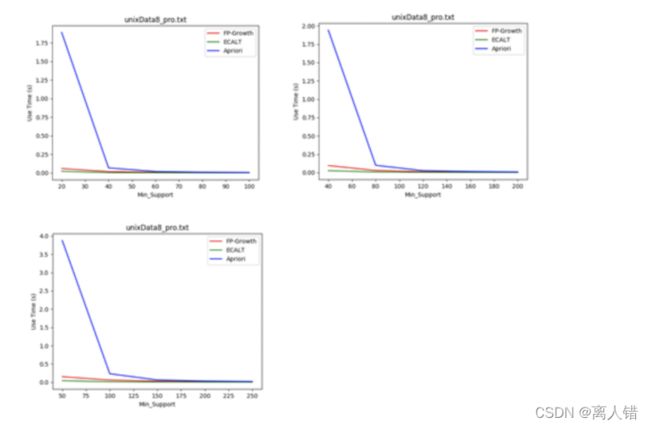
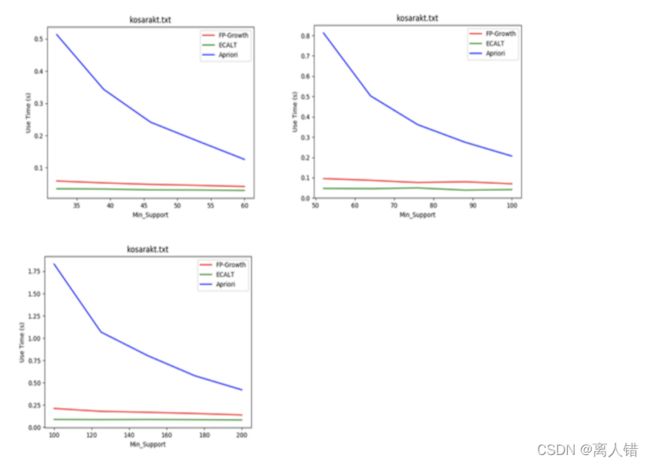
2.最小支持度大小对各方法结果的影响

1）数据集：unixData8    支持度：4% - 20%

 

2）数据集：kosarakt    支持度：1% - 2%

 

结论：

1）最小支持度越小，各个算法所花费的时间越多,且Apriori算法效率最差；Apriori算法候选项集较多，扫描数据库次数较多;FP-Growth算法FP树较茂盛，求解模式更多;Eclat算法求交集次数较多

2）随着最小支持度的增加，各个算法的效率逐渐接近，相当于数据量较小的情况。

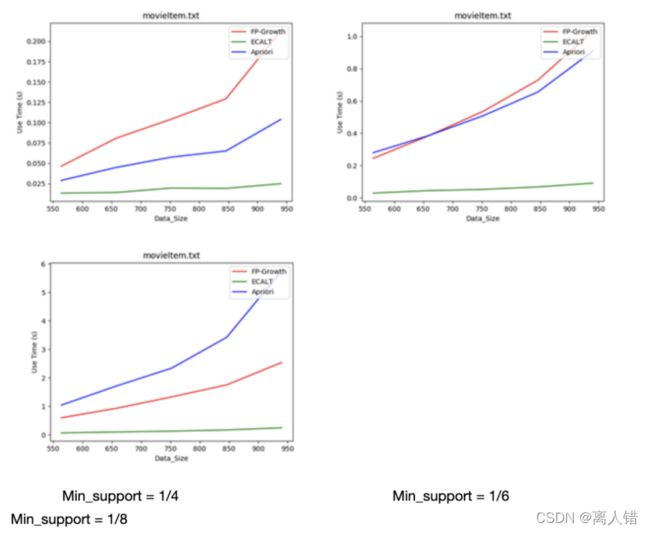
3.不同方法对长事务数据的适用性分析

数据集：movieItem          DataSize = 943

结论：对于长事物的数据集来说

1)最小支持度较大时，生成的FP树深度较大，求解的子问题较多，FP算法性能显著下降，适用性降低；

2)最小支持度较小时，Apriori算法生成大量候选项，扫描数据库次数显著增加，Apriori算法性能显著下降，适用性降低

 

五、实验总结及结果讨论分析

1、Apriori算法的效率最低，因为其需要很多次的扫描数据库；

2、FP—Growth算法在长事物数据上表现很差，因为当事物很长时，树的深度也很大，需要求解的子问题就变得特别多，因此效率会迅速下降；

3、Eclat算法的效率最高，但是由于我们事先使用了递归的思想，当数据量很大的时候会给系统带来巨大的负担，因此不适合数据量很大的情况