R中怎么做加权最小二乘_Stata+R:分位数回归一文读懂
NEW!连享会·推文专辑:
Stata资源 | 数据处理 | Stata绘图 | Stata程序
结果输出 | 回归分析 | 时间序列 | 面板数据 | 离散数据
交乘调节 | DID | RDD | 因果推断 | SFA-TFP-DEA
文本分析+爬虫 | 空间计量 | 学术论文 | 软件工具
连享会学习群-常见问题解答汇总:
? WD 主页:https://gitee.com/arlionn/WD
? 连享会主页:lianxh.cn

连享会 · 名师讲坛
? 空间计量 专题
⌚ 2020.12.10-13? 主讲:杨海生 (中山大学);范巧 (兰州大学)
? 课程主页:https://gitee.com/arlionn/SP

连享会 · 计量专题
? Stata 数据清洗实战系列(第二季)
⌚ 2020.11.28,19:00-21:00,88 元
? 课程主页:https://gitee.com/arlionn/dataclean

谢雁翔 (南开大学),[email protected]
钟舜斌 (北京工商大学),[email protected]
编者按: 本文部分参考了游万海老师的分位数回归讲义和陈强老师的《高级计量经济学及Stata应用》,特此致谢!
目录
1. 引言
1.1 均值回归与条件分布
1.2 分位数回归
2. 分位数回归初识
3. 分位数回归模型与 Stata 实现
3.1 生成随机模拟数据
3.2 分位数模型估计及 Stata 实现
3.3 Wald 检验
3.4 系数可视化
4. 面板分位数回归
4.1 Koenker (2004)
4.2 Canay (2011)
4.3 Machado and Silva (2019)
4.4 Powell (2015)
5. 更多参考资料
1. 引言
在此前的推文中,我们对分位数回归和面板分位数回归都做过简单介绍,参见:
- Stata:分位数回归简介
- Stata: 面板分位数回归
本文通过几篇论文的实操对分位数回归进行更为全面的介绍,内容涉及:分位数回归的基本思想、面板分位数回归、边际效应估计及图示等。
1.1 均值回归与条件分布
一般回归模型中着重考察的是解释变量 对被解释变量 的条件均值 的影响,又可看作「均值回归」,但是 刻画的是条件分布 集中趋势,若 是非对称分布,则 就不能很好地反映整个条件分布。如果能够得到 的重要分位数信息,如 1/4 分位数、中位数、3/4 分位数等,则可以更全面的认识 。
从实际来看,分位数信息也十分重要,比如,在评估某项干预对受众群体的影响时,我们不但希望了解干预的「平均」影响,更希望掌握干预对位于特征分布不同位置 (分布末端或顶端) 人群的「异质性」影响。
1.2 分位数回归
针对样本数据「异质性」特征,常用做法是根据数据特征进行「分组回归」,但这样的做法会导致「样本数据的损失」。为此,Koenker 和 Bassett (1978) 提出「分位数回归 (Quantile Regression, QR)」,并使用残差绝对值的加权平均 (如,) 作为最小化的目标函数,尽可能减小极端值的影响。
由此可知,通过设置不同的分位点,分位数回归模型可以全面的刻画解释变量与被解释变量之间的关系。此外,相比于普通的线性回归 (均值回归),分位数回归的估计结果对「偏态、多峰和异常值数据」更为稳健。
2. 分位数回归初识
对一个随机变量 和任意一个 到 之间的数 , 如果 的取值 满足 ,则 是 的 分位数。上述过程语言表述为,在某个样本集中,从小至大排列之后,小于某值的样本子集占总样本集的比例。
有一组数据 ,如何找到一个数 ,使得其和 中的元素尽可能的接近?—— 求数据的「集中趋势: 平均值」。更一般地,设 为最靠近该组数据的中心,则最小化残差平方和就是样本均值。
即:
对 求偏导,得:
可得:
将标量 换成自变量 的线性方程 , 则有:
令 ,上式则变换为:
对应参数 的解即为线性回归模型 的估计值。
(1) 如果损失函数定义为二次函数 ,那么 ,即 对应的解则为最小二乘估计的解。
(2) 如果损失函数定义为 ,那么 ,即 对应的解则为最小一乘估计的解。
(3) 如果损失函数定义为:
则:
即为对应下式的解:
损失函数就是上述例子中模型所表现的误差,最小化损失函数的过程其实是通过损失函数反过来优化模型参数。设分位点 = 0.9,则损失函数为:
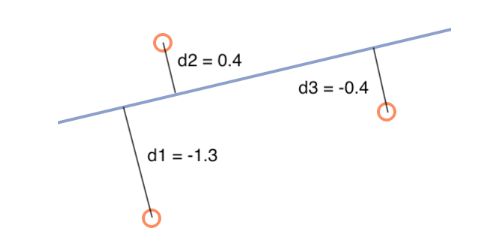
当 =0.5 时候就是最小一乘回归。根据损失函数的形式,我们知道最小二乘回归和最小一乘回归的损失函数图像是关于 轴对称的,但是其他分位数的损失函数不一定对称,即对不同的分位点,高估和低估其预测值会有不同的损失权重。例如,对于0.25 分位数,高估 的损失权重为 0.75, 而低估的权重为 0.25;对于 0.75 分位数,则情况正好相反。可以直观理解为,越高的分位数估计,越倾向于高估预测值,越低的分位数则倾向于低估预测值。
在实际运用中,选择不对称的分位数损失函数往往可以反映因变量的分位数分布,不同分位数的分布可能由于各种原因存在差异。目前,分位回归模型的估计算法主要有单纯形法、内点算法和平滑算法。
3. 分位数回归模型与 Stata 实现
3.1 生成随机模拟数据
clear
set seed 1 //设置种子值,保证结果可重复
qui set obs 100 //设置100观测值
egen x = seq(), from(1) to(100) //生成1到100序列
gen sig = 0.1 + 0.05*x //sig代表方差,方差随着x在变化,不是同方差,异方差不对称
scalar b_0 = 6
scalar b_1 = 0.1
gen e = rnormal(0,sig) //生成误差项
gen y = b_0 + b_1*x + e
twoway scatter y x, plotregion(fcolor(white)) graphregion(fcolor(white))
*散点图呈现喇叭状,非均匀分布考虑分位数回归,若均匀分布不考虑分位数回归
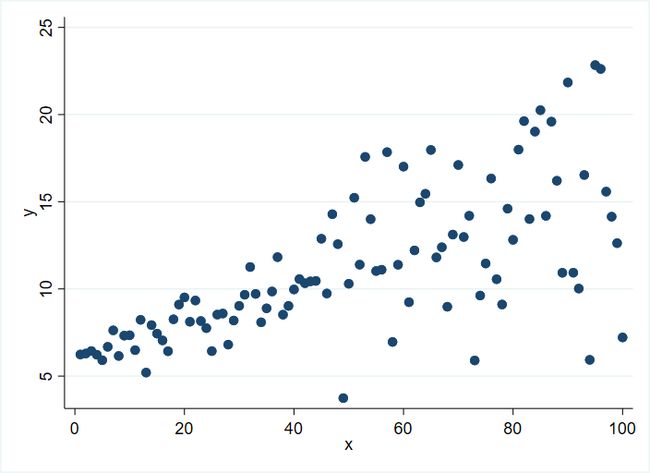
从上图可以看出,随着 的增大, 的波动性越大,这违反了线性回归模型 (OLS) 的同方差假定,此时普通线性回归模型不再适用。
3.2 分位数模型估计及 Stata 实现
分位数回归模型的基本步骤:
绘制散点图,判断数据分布 (对称/非对称) 是否适合于用分位数回归模型;
建模估计
qreg,sqreg,bsqreg,qreg2(聚类稳健标准误);系数差异性检验 wald 检验;
系数可视化
grqreg。
在 Stata 的进行分位数回归估计的命令中,sqreg 较为常用,详见 help sqreg。
*计算单个分位点
sysuse auto, clear
qreg price weight length foreign, quantile(.25)
est store m0
*多个分位点,从0.3-0.9,可用qreg的循环语句也可使用sqreg命令
forvalues i = 0.3(0.3)0.9{
qreg price weight length foreign, quantile(`i')
local j = `i' * 10
local j = int(`j')
est store m`j'
}
local m "0.25RQ 0.3RQ 0.6RQ 0.9RQ"
esttab m0 m3 m6 m9, mtitle(`m') nogaps star(* 0.1 ** 0.05 *** 0.01)
----------------------------------------------------------------------------
(1) (2) (3) (4)
0.25RQ 0.3RQ 0.6RQ 0.9RQ
----------------------------------------------------------------------------
weight 1.832*** 1.705** 5.975*** 9.666***
(2.89) (2.59) (4.00) (4.53)
length 2.846 5.090 -100.1* -248.8***
(0.13) (0.23) (-1.96) (-3.40)
foreign 2209.9*** 2148.6*** 3731.0*** 4164.4***
(5.24) (4.90) (3.75) (2.93)
_cons -1879.8 -1843.9 5901.2 25191.0***
(-0.76) (-0.72) (1.01) (3.02)
----------------------------------------------------------------------------
N 74 74 74 74
----------------------------------------------------------------------------
t statistics in parentheses
* p<0.1, ** p<0.05, *** p<0.01
3.3 Wald 检验
不同分位数下系数差异检验用 Wald 检验,具体如下:
假设 为系数, 为 方差协方差矩阵。现在需要做如下假设检验:
相应的 wald 检验统计量为
这个统计量服从卡方分布
其中:q 为待检验的线性假设个数。
set seed 1 //设置种子值
sysuse auto, clear
*sqreg不用循环语句,默认情况下reps为20,bootstrap100次
sqreg price weight length foreign, quantile(.25 .5 .75) reps(100)
*wald检验
test [q25]weight=[q75]weight //检验0.25分位点处与0.75分位点处是否存在显著差异,拒绝原假设则存在差异
(1) [q25]weight - [q75]weight = 0
F( 1, 70) = 11.62
Prob > F = 0.0011
3.4 系数可视化
*ssc install grqreg,all replace //安装外部命令
sysuse auto, clear
qreg price mpg headroom
grqreg, cons ci ols olsci title(Fig.1a Fig.1b Fig.1c) //cons表示常数项绘图,ci表示置信区间,ols表示绘出普通ols,olsci表示ols回归置信区间
Median regression Number of obs = 74
Raw sum of deviations 71102.5 (about 4934)
Min sum of deviations 64549.83 Pseudo R2 = 0.0922
------------------------------------------------------------------------------
price | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mpg | -127.3333 60.78234 -2.09 0.040 -248.5299 -6.136791
headroom | -130.6667 415.6721 -0.31 0.754 -959.4933 698.16
_cons | 8272.333 2158.205 3.83 0.000 3968.995 12575.67
------------------------------------------------------------------------------
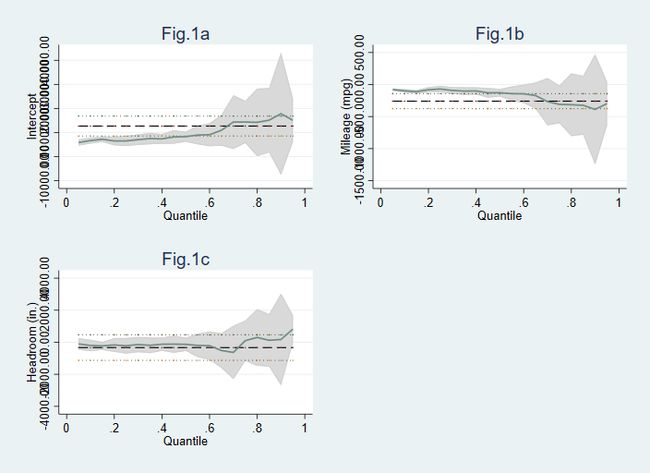
上图分别为 cons (常数项) 、mpg 与 headroom 的分位数估计结果,横轴的虚线为 ols 估计结果及其置信区间。但也存在问题,比如纵轴坐标重叠和背景非白色。
4. 面板分位数回归
面板分位数回归,顾名思义即将截面分位数回归模型扩展至面板数据框架下,考虑了研究单元之间的个体异质性。特别注意的是,面板分位数回归为非线性关系,对于个体效应的估计不能通过 i.id 虚拟变量的形式控制。
4.1 Koenker (2004)
惩罚分位 (Penalized quantile regression with fixed effects),应用了LASSO的思想:
缺点: (1) 当 比较大时,计算费时;(2) 的选择会影响估计结果。
实现:R 中的 rqpd 包进行估计,rqpd不支持 R 3.6.3 及以后版本,建议直接在 R 中运行,更多内容见「rqpd-package: Regression quantiles for panel data」,也可以使用 Stata 外部命令rcall 运行,详细请参考 「Rcall:Stata 与 R 的无缝对接」。
温馨提示: 文中链接在微信中无法打开,请点击
## rcall 可以从Stata中运行R命令,为简便运算可以直接复制粘贴进R运算
install.packages("rqpd", repos="http://R-Forge.R-project.org")
install.packages("plm", repos="http://R-Forge.R-project.org")
library(rqpd) ##加载面板分位数回归包
library(plm) ##加载面板数据回归包
data(Produc,package="plm") ##调用plm包自带数据集进行面板估计
mydata = Produc
m 17 ##17年
n 48 ##美国48州
s 1:n,rep(m,n))) ##声明面板数据结构变量
x ##数据中取出解释变量x
y ##数据中取出被解释变量y
##rqpd直接运算公式,个体效应惩罚系数lambda为1,系统默认分位点是0.25,0.5,0.75
fit 1))
sfit sfit
sfit$coefficients ##能一并取出估计的个体效应系数
##依次定义九个分位点同时定义tau和tauw
fit1 0.1,0.9,by=0.1),tauw=rep(1/9,9),lambda = 1))
sfit1 sfit1
4.2 Canay (2011)
两阶段估计法 (Two-step estimator),分位数回归为非线性运算,面板数据不能通过组内去心的方法解决。
思想:先消除个体效应,再进行估计。与 Koenker (2004) 的相同点:将 设置为 location,即不随分位点改变。实现:作者主页 R 程序,详见「程序」。
温馨提示: 文中链接在微信中无法打开,请点击
4.3 Machado and Silva (2019)
优点:(1) 个体效应允许随着分位点在变动 (location-scale);(2) 可以纳入其他内生解释变量;(3) 计算速度较快。
缺点: 假定变量系数与分位点之间关系是单调的(要不单调上升,要不单调下降),即不存在分位交叉 (No Quantile-Crossing),画图无意义。
实现:Stata 中 xtqreg 进行估计,详细参见 help xtqreg。
关于 xtqreg 系数可视化,请参考以下代码:
clear //清空数据
set obs 100 //设置100观测值
egen country_id = seq(),b(10) //每10个重复构造整数序列,生成变量country_id
bysort country_id: gen time = _n //根据分组country_id生成时间变量
set seed 12345 //设置种子值确保可重复
gen y = uniform() //生成被解释变量y服从正态分布
forv i = 1/8{
gen z`i' = uniform()
} //循环语句生成8个解释变量
local x1 "z1 z2 z3 z4 z5 z6 z7 z8" //局部宏定义所有解释变量
*list `x1' //列出所有被解释变量
local v_num : word count `x1' //利用扩展函数 word count string 得到x1中变量的个数
di `v_num' //v_num表示最大的循环个数,8个
est clear
mat result1 = J(`v_num',1,.) //生成空矩阵result1,8行1列
matrix rownames result1 = `x1' //矩阵行命名为对应的被解释变量
mat list result1 //列出空矩阵
tempname a b b1 //设定临时矩阵变量名
forvalues quantile = 0.1(0.1)0.9 { //从0.1-0.9没隔0.1开始循环
local wanted : di %2.1f `quantile' //列出循环分位点长度设置为2,保留一位小数,定义为`wanted'
local wanted = `wanted'*10 //`wanted'为每一分位点重复十次
xtqreg y `x1', i(country_id) q(`quantile') //面板分位数回归
matrix `a' = r(table) //对应各个分位点估计的`x1'系数
mat list `a' //列出面板分位数回归`a'矩阵
matrix `b' = `a'[1,1..`v_num'] \ `a'[2,1..`v_num'] //仅取出面板分位数回归`a'矩阵的前两行构成`b'矩阵,第一行是系数。第二行是标准误,第四行是p值
mat list `b' //列出`b'矩阵
mat `b1' = `b''
matrix colnames `b1' = b_q`wanted' p_q`wanted' //`b1'为`b'矩阵的转置
mat list `b1' //列出`b1'矩阵
matrix result1 = (result1, `b1') //`b1'数据导入列出空矩阵result1
}
mat list result1
matselrc result1 cresult, c(2/19) //19列 = 2*分位个数+1列无用项(第一列),保留有用数据列
mat list cresult
local newnames : colfullnames cresult
di "`newnames'"
local cn : word count `newnames'
di `cn'
svmat cresult, names(reg) //矩阵数据转换为变量
keep reg*
format reg* %4.3f //设定格式为保留三位小数
drop if reg1==. //删除缺失值,行数为8,8个解释变量:变量为18,对应不同分位点的系数和标准误;
forv i = 1/9 { /*9:分位个数*/
local k1 = 2*`i' - 1 //奇数列为系数
local k2 = 2*`i' //偶数列为标准误
gen up_`i' = reg`k1' + 1.96*reg`k2' //上界
gen low_`i' = reg`k1' - 1.96*reg`k2' //下界
}
preserve
keep reg1 reg3 reg5 reg7 reg9 reg11 reg13 reg15 reg17 //保留系数列
rename (reg1 reg3 reg5 reg7 reg9 reg11 reg13 reg15 reg17) (reg1 reg2 reg3 reg4 reg5 reg6 reg7 reg8 reg9) //重命名
xpose,clear //转置数据
renvars v*, prefix(coef_) //重命名加前缀coef_
save coef.dta,replace //储存系数数据
restore //preserve+restore运行不保存
keep up* low* //保留上下界数据
xpose,clear //转置数据
preserve
keep if mod(_n,2)==1 //保留奇数行作为上界数据
renvars v*, prefix(up_) //重命名加前缀up_
save up.dta,replace //储存上界数据
restore
preserve
keep if mod(_n,2)==0 //保留偶数行作为下界数据
renvars v*, prefix(low_) //重命名加前缀low_
save low.dta,replace //储存下界数据
restore
use up.dta,clear //打开上界数据
merge 1:1 _n using low.dta //一对一合并数据
keep if _merge==3 //合并匹配成功为_merge==3,保留合并成功行
drop _merge //删除合并信息
merge 1:1 _n using coef.dta //一对一合并数据
keep if _merge==3
drop _merge //删除合并信息
matrix input myrvec = (0.10,0.20,0.30,0.40,0.50,0.60,0.70,0.80,0.90)
mat list myrvec
mat qq = myrvec' //qq矩阵为myrvec的转置
mat list qq
svmat qq, names(qqp) //矩阵数据转换为变量
forv i = 1/8{
twoway (line up_v`i' qqp,lc(black*1.4) lpattern(dash) xlabel(0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90)) ///
(line low_v`i' qqp,lc(black*1.4) lpattern(dash) xlabel(0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90)) ///
(line coef_v`i' qqp, lc(black*2) lw(thick)) ,xtitle("Quantile") ytitle("Coefficient(z`i')") plotregion(margin(zero)) graphregion(color(white)) legend(off)
graph save g_`i'
}
graph combine g_1.gph g_2.gph g_3.gph g_4.gph g_5.gph g_6.gph g_7.gph g_8.gph
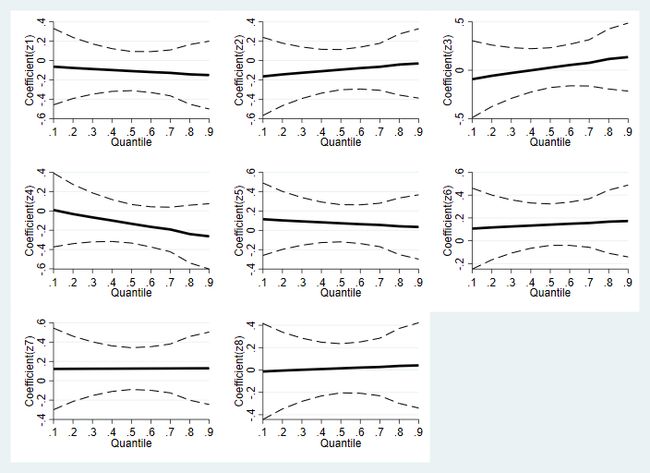
4.4 Powell (2015)
qregpd 估计是实现广义分位数估计 genqreg 的特例,其解决了由其他固定效应分位数估计引起的一个基本问题:包含个体固定效应会改变对处理变量的估计系数的解释。由于标准差的计算有时可能收极值的影响,可以使用 MCMC 方法或网格搜索方法来估计广义分位数回归。关于该命令更多详细介绍,请参考 help qregpd。相关代码如下:
*ssc install qregpd, replace
*ssc install moremata, replace
sysuse nlswork, clear
qregpd ln_wage tenure union, id(idcode) fix(south)
estimates store QREG1
matrix list e(gamma) //显示south固定效应估计值
qregpd ln_wage tenure union, id(idcode) fix(year)
estimates store QREG2
matrix list e(gamma) //显示year时点固定效应估计值
*带工具变量的情形--采用MCMC优化
*tenure为内生变量,union为外生变量做自己的工具变量,ttl_exp wks_work为工具变量
qregpd ln_wage tenure union, id(idcode) fix(year) optimize(mcmc) draws(1000) burn(100) arate(.5) noisy instruments(ttl_exp wks_work union)
mat list e(gamma)
*估计1/4分位数的结果--默认是0.5
qregpd ln_wage tenure union, q(0.25) id(idcode) fix(year) optimize(mcmc) draws(1000) burn(100) arate(.5) noisy instruments(ttl_exp wks_work union)
mat list e(gamma)
5. 更多参考资料
- [1] 连享会直播课程:分位数回归 (游万海) -Link-
- 连享会直播:分位数回归
- 连享会推文:Stata:分位数回归简介
- 连享会推文:Stata: 面板分位数回归
- [2] 分位数回归及Stata实现 -Link-
- [3] You, Wan-Hai, et al. Democracy, Financial Openness, and Global Carbon Dioxide Emissions: Heterogeneity Across Existing Emission Levels. World Development, vol. 66, 2015, pp. 189–207. -Link-
- [4] You, Wanhai, et al. Oil Price Shocks, Economic Policy Uncertainty and Industry Stock Returns in China: Asymmetric Effects with Quantile Regression. Energy Economics, vol. 68, 2017, pp. 1–18. -Link-
- [5] You, Wanhai, et al. Twitter’s Daily Happiness Sentiment and the Predictability of Stock Returns. Finance Research Letters, vol. 23, 2017, pp. 58–64. -Link-
- [6] Chuang, C.C., Kuan, C.M., Lin, H.Y., 2009. Causality in quantiles and dynamic stock return volume relations.Journal of Banking & Finance. 33, 1351–1360. -Link-
- [7] Xiao, Z. 2009. Quantile cointegrating regression. Journal of Econometrics, 150(2), 248-260. -Link-
- [8] White, H., Kim, T. H., & Manganelli, S. 2015. VAR for VaR: Measuring tail dependence using multivariate regression quantiles. Journal of Econometrics, 187(1), 169-188. -Link-
- [9] Cho, J. S., Kim, T. H., & Shin, Y. 2015. Quantile cointegration in the autoregressive distributed-lag modeling framework. Journal of Econometrics, 188(1), 281-300. -Link-
- [10] Koenker, R. (2004). Quantile Regression for Longitudinal Data, Journal of Multivariate Analysis, 91, 74–89. -Link-
- [11] Canay, I.A. (2011). A Simple Approach to Quantile Regression for Panel Data, The Econometrics Journal, 14, 368–386. -Link-
- [12] Machado, J.A.F. and Santos Silva, J.M.C. (2019), Quantiles via Moments, Journal of Econometrics, 213(1), pp. 145-173. -Link-
- [13] Powell, David. 2015. Quantile Regression with Nonadditive Fixed Effects. RAND Labor and Population Working Paper. -Link-
- [14] Powell, David. 2016. Quantile Treatment Effects in the Presence of Covariates. RAND Labor and Population Working Paper. -Link-
? 空间计量 专题 ⌚ 2020.12.10-13
? 主讲:杨海生 (中山大学);范巧 (兰州大学)
? 课程主页:https://gitee.com/arlionn/SP

免费公开课:
- 直击面板数据模型:https://gitee.com/arlionn/PanelData - 连玉君,时长:1小时40分钟
- Stata 33 讲:https://gitee.com/arlionn/stata101 - 连玉君, 每讲 15 分钟.
- Stata 小白的取经之路:https://gitee.com/arlionn/StataBin - 龙志能, 2 小时
- 部分直播课课程资料下载 ? https://gitee.com/arlionn/Live (PPT,dofiles等)
温馨提示: 文中链接在微信中无法生效,请点击底部
关于我们
- ? 连享会 ( 主页:lianxh.cn ) 由中山大学连玉君老师团队创办,定期分享实证分析经验。
- ? 直达连享会:【百度一下:连享会】即可直达连享会主页。亦可进一步添加 主页,知乎,面板数据,研究设计 等关键词细化搜索。
 连享会主页 lianxh.cn
连享会主页 lianxh.cn
? 连享会小程序:扫一扫,看推文,看视频……

? 扫码加入连享会微信群,提问交流更方便

? 连享会学习群-常见问题解答汇总:
? https://gitee.com/arlionn/WD
