RANSAC平面拟合理论和代码---PCL源码笔记
RANSAC平面拟合理论和代码—PCL源码笔记
RANSAC平面拟合的原理,首先知道如何定义平面,求平面的方程,求平面的法向量,以及求点到平面的距离。 其次,需要了解RANSAC的原理和公式。
一、平面相关定义
我们知道 A x + B y + C z + d = 0 Ax+By+Cz+d=0 Ax+By+Cz+d=0 是平面方程的定义。 我们知道,三个点是可以形成一个平面的,因此如果给定三个点,假设 p 0 , p 1 , p 2 p_0, p_1, p_2 p0,p1,p2, 求这三个点所形成的平面,可根据以下步骤:
-
求两点之间的向量 p 1 p 0 ⃗ , p 2 p 0 ⃗ \vec{p_1p_0}, \vec{p_2 p_0} p1p0,p2p0
p 1 p 0 = p 1 − p 0 = ( l , m , n ) p 2 p 0 = p 2 − p 0 = ( o , p , q ) p_1 p_0 = p_1 - p_0 = (l, m, n)\\ p_2 p_0 = p_2 - p_0 = (o, p, q) p1p0=p1−p0=(l,m,n)p2p0=p2−p0=(o,p,q) -
求两向量的向量积,即 p 1 p 0 ⃗ × p 2 p 0 ⃗ \vec{p_1p_0} \times \vec{p_2 p_0} p1p0×p2p0
p 1 p 0 ⃗ × p 2 p 0 ⃗ = ( m q − n p , n o − l q , l p − m o ) \vec{p_1p_0} \times \vec{p_2 p_0} = (mq-np, no-lq, lp-mo) p1p0×p2p0=(mq−np,no−lq,lp−mo) -
所得向量积即为平面方程 A x + B y + C z + d = 0 Ax+By+Cz+d=0 Ax+By+Cz+d=0的法向量
A = m q − n p B = n o − l q C = l p − m o d = − ( A x 0 + B y 0 + C z 0 ) A = mq-np \\ B = no-lq \\ C = lp-mo \\ d = - (Ax_0+ By_0 + Cz_0) A=mq−npB=no−lqC=lp−mod=−(Ax0+By0+Cz0) -
点到平面的距离
先来看一下向量在轴上的投影:
设A,B 两点 x x x 轴上的投影分别为 A 1 , B 1 A_1, B_1 A1,B1, 则向量 A 1 B 1 ⃗ \vec{A_1B_1} A1B1的长度 ∣ ∣ A 1 B 1 ⃗ ∣ ∣ ||\vec{A_1B_1}|| ∣∣A1B1∣∣成为向量 A B ⃗ \vec{AB} AB在 x x x轴上的投影,记为 P r j x A 1 B 1 ⃗ Prj_x \vec{A_1B_1} PrjxA1B1。设 A 1 B 1 ⃗ \vec{A_1 B_1} A1B1。设 A B ⃗ \vec{AB} AB与 x x x轴之间夹角为 α \alpha α, 则P r j x A B ⃗ = ∣ ∣ A 1 B 1 ⃗ ∣ ∣ = ∣ A B ⃗ ∣ ∣ c o s α Prj_x \vec{AB} = ||\vec{A_1B_1}|| = |\vec{AB}|| cos \alpha PrjxAB=∣∣A1B1∣∣=∣AB∣∣cosα
点到平面的距离计算
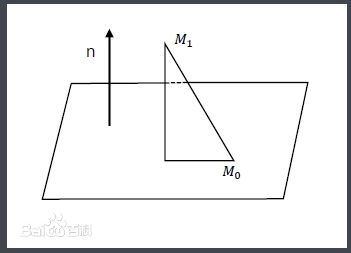
向量法计算点到平面的距离,就是把点和平面放在直角坐标系下进行计算。这样,点和平面均可用坐标来表示(如图1所示)。假设平面方程为:
A x + B y + C z + d = 0 Ax+By+Cz+d=0 Ax+By+Cz+d=0设向量 n ⃗ = ( A , B , C ) \vec{n} = (A, B, C) n=(A,B,C) 为 平面的法向量,平面外一点 M 1 M_1 M1,坐标为 ( x 1 , y 1 , z 1 ) (x_1, y_1, z_1) (x1,y1,z1), 在平面上取一点 M 0 M_0 M0,则点 M 1 M_1 M1到平面的距离 d d d为:
d = P r j n ⃗ M 0 M 1 ⃗ = ∣ ∣ M 0 M 1 ⃗ ∣ ∣ c o s α d= Prj_{\vec{n}} \vec{M_0 M_1} = ||\vec{M_0 M_1}|| cos \alpha d=PrjnM0M1=∣∣M0M1∣∣cosα
其中 α \alpha α为向量 n ⃗ \vec{n} n与向量 M 0 M 1 ⃗ \vec{M_0 M_1} M0M1的夹角,
cos α = M 0 M 1 ⃗ ⋅ n ⃗ ∣ ∣ M 0 M 1 ⃗ ∣ ∣ ⋅ ∣ ∣ n ⃗ ∣ ∣ \cos \alpha = \frac{\vec{M_0 M_1} \cdot \vec{n}} {||\vec{M_0 M_1}|| \cdot ||\vec{n}||} cosα=∣∣M0M1∣∣⋅∣∣n∣∣M0M1⋅n
因此,
d = M 0 M 1 ⃗ ⋅ n ⃗ ∣ ∣ n ⃗ ∣ ∣ d= \frac{\vec{M_0 M_1} \cdot \vec{n} }{||\vec{n}||} d=∣∣n∣∣M0M1⋅n
二、RANSAC原理
理解完平面的定义,法向量求解和点到平面的距离,我们就可以继续探讨RANSAC拟合平面的关键算法: RANSAC算法。
RANSAC算法有以下步骤:
- 随机选取三个点,根据平面方程 A x + B y + C z + d = 0 Ax+By+Cz+d=0 Ax+By+Cz+d=0, 计算模型参数。
- 用剩余的点计算到该平面方程的距离,将距离与所设定的阈值做比较,如果小于,则该点为内点;否则为外点。统计该参数模型下内点的个数。
- 继续执行上面两步,若当前模型的内点数量大于已经保存的最大内点数量,则变更新的模型参数,保留模型参数始终是内点数量最多的模型参数。
- 重复上述三步,不断迭代,直到达到迭代阈值,找到内点个数最多的模型参数,最后用内点再次对模型参数进行估计,从而得到最终的模型参数。
上面有个阈值需要关注,迭代阈值。 我们如何知道迭代的次数呢?其实,这个值是可以估算出来的:
假设内点在数据中的占比为 p p p,那么每次计算模型使用 k k k个点的情况下,选取点为内点的概率为 p k p^k pk,选取的点为外点的概率为 1 − p k 1-p^k 1−pk, 因此尝试 S S S次失败的概率为:
1 − P = ( 1 − p k ) S 1-P = (1-p^k)^S 1−P=(1−pk)S
都为内点的概率为:
P = 1 − ( 1 − p k ) S P = 1- (1-p^k)^S P=1−(1−pk)S
通过上面的式子,得到最终需要尝试的次数为:
S = log ( 1 − P ) log ( 1 − p k ) S = \frac{\log(1-P)}{\log(1-p^k)} S=log(1−pk)log(1−P)
但是,通常一开始我们无法知道内点在数据中的占比 p p p这个先验,因此可以使用自适应迭代次数的方法。也就是一开始设定一个无穷大的迭代次数,然后每次更新模型参数估计的时候,用当前的内点比值当成 p p p来估算出迭代次数。 又或者设置一个最大的迭代数,但是往往可能无法达到最优解。
三、PCL平面拟合
PCL官方使用RANSAC你和平面的模板。
pcl::ModelCoefficients::Ptr coefficients (new pcl::ModelCoefficients);
pcl::PointIndices::Ptr inliers (new pcl::PointIndices);
// Create the segmentation object
pcl::SACSegmentation seg;
seg.setModelType (pcl::SACMODEL_PLANE);
seg.setMethodType (pcl::SAC_RANSAC);
seg.setDistanceThreshold (0.01);
seg.setInputCloud (cloud);
seg.segment (*inliers, *coefficients);
步骤如下:
1. 定义平面模型参数,和内点索引。
2. 声明分割模型,并设置模型的类别PLANE,拟合模型的方法RANSAC,距离阈值0.01。
3. 设置输入,并获得结果。
1. segment函数
主要关注一下segment这个模板函数,在PCL源码中的sac_segmentation.hpp文件里。下面进行了精简,方便理解。
template <typename PointT> void
pcl::SACSegmentation<PointT>::segment (PointIndices &inliers, ModelCoefficients &model_coefficients){
// Copy the header information
inliers.header = model_coefficients.header = input_->header;
...
// 计算模型
if (!sac_->computeModel (0))
{
PCL_ERROR ("[pcl::%s::segment] Error segmenting the model! No solution found.\n", getClassName ().c_str ());
deinitCompute ();
inliers.indices.clear (); model_coefficients.values.clear ();
return;
}
// 获取内点
sac_->getInliers (inliers.indices);
// 获取模型参数
Eigen::VectorXf coeff (model_->getModelSize ());
sac_->getModelCoefficients (coeff);
// 如果用户需要优化模型参数
if (optimize_coefficients_)
{
Eigen::VectorXf coeff_refined (model_->getModelSize ());
model_->optimizeModelCoefficients (inliers.indices, coeff, coeff_refined);
model_coefficients.values.resize (coeff_refined.size ());
memcpy (&model_coefficients.values[0], &coeff_refined[0], coeff_refined.size () * sizeof (float));
// Refine inliers
model_->selectWithinDistance (coeff_refined, threshold_, inliers.indices);
}else
{
model_coefficients.values.resize (coeff.size ());
memcpy (&model_coefficients.values[0], &coeff[0], coeff.size () * sizeof (float));
}
...
}
2. computeModel函数
上面的平面拟合计算主要在sac_->computeModel (0)这一句。也就是在computeModel这个模板函数,在PCL源码ransac.hpp中实现。为了方便阅读理解,精简了源码。
template <typename PointT> bool
pcl::RandomSampleConsensus<PointT>::computeModel (int)
{
// Warn and exit if no threshold was set
if (threshold_ == std::numeric_limits<double>::max())
{
PCL_ERROR ("[pcl::RandomSampleConsensus::computeModel] No threshold set!\n");
return (false);
}
iterations_ = 0;
std::size_t n_best_inliers_count = 0;
double k = std::numeric_limits<double>::max();
Indices selection;
Eigen::VectorXf model_coefficients (sac_model_->getModelSize ());
const double log_probability = std::log (1.0 - probability_);
const double one_over_indices = 1.0 / static_cast<double> (sac_model_->getIndices ()->size ());
unsigned skipped_count = 0;
// suppress infinite loops by just allowing 10 x maximum allowed iterations for invalid model parameters!
const unsigned max_skip = max_iterations_ * 10;
int threads = threads_;
// Iterate
while (true) // infinite loop with four possible breaks
{
// Get X samples which satisfy the model criteria
// 随机获取样本
{
sac_model_->getSamples (iterations_, selection); // The random number generator used when choosing the samples should not be called in parallel
}
if (selection.empty ())
{
PCL_ERROR ("[pcl::RandomSampleConsensus::computeModel] No samples could be selected!\n");
break;
}
// Search for inliers in the point cloud for the current plane model M
// 计算模型参数
if (!sac_model_->computeModelCoefficients (selection, model_coefficients)) // This function has to be thread-safe
{
//++iterations_;
unsigned skipped_count_tmp;
skipped_count_tmp = ++skipped_count;
if (skipped_count_tmp < max_skip)
continue;
else
break;
}
// Select the inliers that are within threshold_ from the model
//sac_model_->selectWithinDistance (model_coefficients, threshold_, inliers);
//if (inliers.empty () && k > 1.0)
// continue;
// 计算点到平面的距离
std::size_t n_inliers_count = sac_model_->countWithinDistance (model_coefficients, threshold_); // This functions has to be thread-safe. Most work is done here
std::size_t n_best_inliers_count_tmp;
n_best_inliers_count_tmp = n_best_inliers_count;
if (n_inliers_count > n_best_inliers_count_tmp) // This condition is false most of the time, and the critical region is not entered, hopefully leading to more efficient concurrency
{
// Better match ?
if (n_inliers_count > n_best_inliers_count)
{
n_best_inliers_count = n_inliers_count; // This write and the previous read of n_best_inliers_count must be consecutive and must not be interrupted!
n_best_inliers_count_tmp = n_best_inliers_count;
// Save the current model/inlier/coefficients selection as being the best so far
model_ = selection;
model_coefficients_ = model_coefficients;
// Compute the k parameter (k=std::log(z)/std::log(1-w^n))
// 计算迭代次数 k
const double w = static_cast<double> (n_best_inliers_count) * one_over_indices;
double p_no_outliers = 1.0 - std::pow (w, static_cast<double> (selection.size ()));
p_no_outliers = (std::max) (std::numeric_limits<double>::epsilon (), p_no_outliers); // Avoid division by -Inf
p_no_outliers = (std::min) (1.0 - std::numeric_limits<double>::epsilon (), p_no_outliers); // Avoid division by 0.
k = log_probability / std::log (p_no_outliers);
}
}
int iterations_tmp;
double k_tmp;
iterations_tmp = ++iterations_;
k_tmp = k;
if (iterations_tmp > k_tmp)
break;
if (iterations_tmp > max_iterations_)
{
PCL_DEBUG ("[pcl::RandomSampleConsensus::computeModel] RANSAC reached the maximum number of trials.\n");
break;
}
} // while
if (model_.empty ())
{
PCL_ERROR ("[pcl::RandomSampleConsensus::computeModel] RANSAC found no model.\n");
inliers_.clear ();
return (false);
}
// Get the set of inliers that correspond to the best model found so far
sac_model_->selectWithinDistance (model_coefficients_, threshold_, inliers_);
return (true);
}
3. computeModelCoefficients函数
然后可以看到,computeModelCoefficients 函数,就是用于计算平面参数的,即平面法向量,和上面的理论一一对应:
template <typename PointT> bool
pcl::SampleConsensusModelPlane<PointT>::computeModelCoefficients (
const Indices &samples, Eigen::VectorXf &model_coefficients) const
{
// Need 3 samples
if (samples.size () != sample_size_)
{
PCL_ERROR ("[pcl::SampleConsensusModelPlane::computeModelCoefficients] Invalid set of samples given (%lu)!\n", samples.size ());
return (false);
}
pcl::Array4fMapConst p0 = (*input_)[samples[0]].getArray4fMap ();
pcl::Array4fMapConst p1 = (*input_)[samples[1]].getArray4fMap ();
pcl::Array4fMapConst p2 = (*input_)[samples[2]].getArray4fMap ();
// Compute the segment values (in 3d) between p1 and p0
Eigen::Array4f p1p0 = p1 - p0;
// Compute the segment values (in 3d) between p2 and p0
Eigen::Array4f p2p0 = p2 - p0;
// Avoid some crashes by checking for collinearity here
Eigen::Array4f dy1dy2 = p1p0 / p2p0;
if ( p2p0.isZero() || ((dy1dy2[0] == dy1dy2[1]) && (dy1dy2[2] == dy1dy2[1])) ) // Check for collinearity
{
return (false);
}
// Compute the plane coefficients from the 3 given points in a straightforward manner
// calculate the plane normal n = (p2-p1) x (p3-p1) = cross (p2-p1, p3-p1)
model_coefficients.resize (model_size_);
model_coefficients[0] = p1p0[1] * p2p0[2] - p1p0[2] * p2p0[1];
model_coefficients[1] = p1p0[2] * p2p0[0] - p1p0[0] * p2p0[2];
model_coefficients[2] = p1p0[0] * p2p0[1] - p1p0[1] * p2p0[0];
model_coefficients[3] = 0.0f;
// Normalize
model_coefficients.normalize ();
// ... + d = 0
model_coefficients[3] = -1.0f * (model_coefficients.template head<4>().dot (p0.matrix ()));
PCL_DEBUG ("[pcl::SampleConsensusModelPlane::computeModelCoefficients] Model is (%g,%g,%g,%g).\n",
model_coefficients[0], model_coefficients[1], model_coefficients[2], model_coefficients[3]);
return (true);
}
4. countWithinDistance函数
得到平面方程之后,需要计算点到平面的距离 countWithinDistance函数。
template <typename PointT> std::size_t
pcl::SampleConsensusModelPlane<PointT>::countWithinDistance (
const Eigen::VectorXf &model_coefficients, const double threshold) const
{
// Needs a valid set of model coefficients
if (!isModelValid (model_coefficients))
{
PCL_ERROR ("[pcl::SampleConsensusModelPlane::countWithinDistance] Given model is invalid!\n");
return (0);
}
return countWithinDistanceStandard (model_coefficients, threshold);
}
pcl::SampleConsensusModelPlane<PointT>::countWithinDistanceStandard (
const Eigen::VectorXf &model_coefficients, const double threshold, std::size_t i) const
{
std::size_t nr_p = 0;
// Iterate through the 3d points and calculate the distances from them to the plane
for (; i < indices_->size (); ++i)
{
// Calculate the distance from the point to the plane normal as the dot product
// D = (P-A).N/|N|
Eigen::Vector4f pt ((*input_)[(*indices_)[i]].x,
(*input_)[(*indices_)[i]].y,
(*input_)[(*indices_)[i]].z,
1.0f);
if (std::abs (model_coefficients.dot (pt)) < threshold)
{
nr_p++;
}
}
return (nr_p);
}
值得注意的是,这里只有dot product,而公式:
d = M 0 M 1 ⃗ ⋅ n ⃗ ∣ ∣ n ⃗ ∣ ∣ d= \frac{\vec{M_0 M_1} \cdot \vec{n} }{||\vec{n}||} d=∣∣n∣∣M0M1⋅n
是有 n ⃗ ∣ ∣ n ⃗ ∣ ∣ \frac{\vec{n}}{||\vec{n}||} ∣∣n∣∣n,而代码中没有是因为computeModelCoefficients函数中已经normalize法向量了。
Conclusion
至此,RANSAC 平面拟合的理论和相关的PCL源码学习到此了。但是RANSAC经过了那么多年的发展,已经衍生了很多优化版本。以后有机会会继续学习的。
Reference
- PCL平面分割, https://pcl.readthedocs.io/projects/tutorials/en/master/planar_segmentation.html#planar-segmentation
- 点到平面距离, https://baike.baidu.com/item/%E7%82%B9%E5%88%B0%E5%B9%B3%E9%9D%A2%E8%B7%9D%E7%A6%BB/10690055?fr=aladdin