信息检索导论 第十七章十八章知识点
层次聚类
层次聚类(hierarchical clustering或hierarchic clustering)会输出一个具有层次结构的簇集合,可以是自顶向下或自底向上的一个过程。自底向上(HAC)的算法一开始将每篇文档都看成是一个簇,然后不断地对簇进行两两合并(或称凝聚(agglomerate)),直到所有文档都聚成一类为止。而自顶向下的方法则首先将所有文档看成一个簇,然后不断利用某种方法对簇进行分裂直到每篇文档都成为一个簇为止。
下图是HAC聚类的树状图表示。聚类过程中的每次合并都表示成一条水平线,而y轴对应的是合并时两个簇的相似度,这个相似度也被称为合并后的簇的结合相似度(combination similarity),由计算两个簇相似度的不同定义,我们得到不同的层次聚类方法。

注意到 HAC 的一个基本假设是,HAC 聚类中的合并操作是单调的(monotonic)。这里的单调性意味着,每次合并的结合相似度都是目前所有簇之间结合相似度最高的,优先合并最相似的两个簇。从上图我们可以看出这个假设。
如果我们希望像扁平聚类一样得到不相交的多个簇,可以在层次结构中的某一点上进行截断(即停止聚类),截断点的确定方法则有如下多种做法。
1.在某个事先给定的相似度水平上进行截断
2.当两个连续的聚类结果的结合相似度之差最大时进行截断
3.应用公式进行截断
K = arg min K [ R s s ( K ) + λ K ] K=\arg \min _{K}\left[ Rss\left( K\right) +\lambda K\right] K=argKmin[Rss(K)+λK]
4.事先指定结果簇的数目 K,在产生 K 个簇时进行截断
四种凝聚式层次聚类算法
四种 HAC 算法中所使用了不同的簇相似度概念。
单链接聚类算法
在单连接聚类(single-link clustering或single-linkage clustering)中,两个簇之间的相似度(结合相似度) 定义为两个最相似的成员之间的相似度。单连接的合并准则是局部的 (local),即它仅仅关注两个簇互相邻近的区域,而不考虑簇中更远的区域和簇的总体结构。
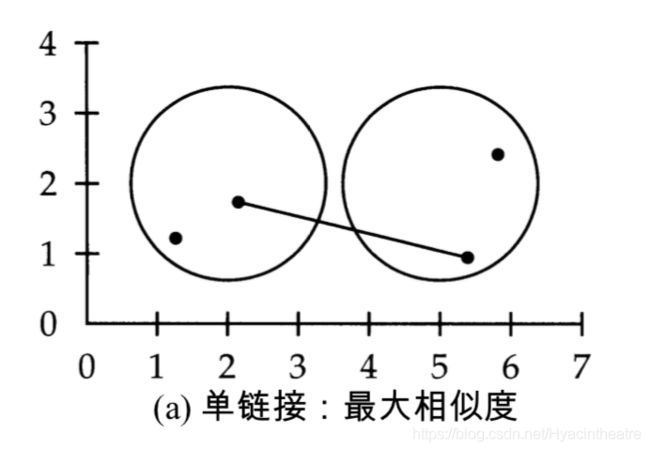
该合并准则的局部性要求非常严格,一连串的多个点有可能会合并成一个长链,而不会考虑合并后的簇的整体形状。这种效果称为链化(chaining),如下图。
全连接聚类算法
在全连接聚类(complete-link clustering 或 complete-linkage clustering)中,两个簇之间的相似度(结合相似度) 定义为两个最不相似的成员之间的相似度,这也相当于选择两个簇进行聚类,使得合并结果具有最短直径。全连接聚类准则是非局部的,聚类结果中的整体结构信息会影响合并的结果。

该方法可能会对离群点较为敏感,比如某个远离中心的文档会显著改变最后的聚类结果。下图中,我们当然认为后四个文档分到一类比较合理。

组平均凝式聚类
GAAC(Group-average Agglomerative Clustering,组平均凝式聚类)通过计算所有文档之间相似度的平均值 SIM-GA来聚类,其中也包括来自同一簇的文档。这里文档间的相似度用内积计算。求平均的做法可以避免在单连接和全连接准则中只计算一对文档相似度的缺陷。

注意到组平均凝式聚类没有使用自相关度。
质心聚类
在质心聚类中,将通过两个簇的质心相似度来定义这两个簇的相似度。
我们把括号打开,两个求和符号放在前面,会发现质心相似度等价于不同簇文档之间的平均相似度。因此,GAAC 和质心聚类的区别在于,GAAC 在计算平均相似度时考虑了所有文档之间的相似度,而质心聚类中仅仅考虑来自不同簇的文档之间的相似度。
下图表明,质心聚类有时会违反HAC的单调性假设。如果我们把距离的相反数看作相似度,我们看到第二次合并时的结合相似度大于第一次合并时的结合相似度,导致树状图中直线的交叉。

总结四种HAC聚类,如下表:

簇标签生成
在扁平聚类和层次聚类的很多应用特别是分析任务和用户界面中, 人们需要和簇进行交互。这种情况下,必须要对簇生成标签,以便让用户对簇的相关内容有所了解。
- 差别式簇标签生成(differential cluster labeling)方法
该方法通过比较某个簇和其他簇中的词项 分布情况 来对簇进行标识。比如互信息(13.5节)以及开方等方法都可以找出能够刻画本簇与其他簇差异的簇标签。
互信息衡量了一个词项对于一个类来说有多少信息,我们可以选出对于这个簇互信息高的几个词项作为簇标签。 - 基于簇内信息的标签生成(cluster-internal labeling)方法
该方法只根据簇本身计算出标签。一种做法是用最接近簇质心的文档标题作为簇标签。另一种选择簇质心中一些具有较高权重的词项作为簇标签。因为质心向量是一个簇内的文档向量求平均得到的,所以它的维度是词项的个数,每一维代表一个词。
标题比一系列词项的可读性要强,并且完整的标题也可以包含上下文信息,而这是利用 MI (互信息)选择得到的前 10 个词项所不能包含的。然而,单篇文档不可能代表簇中的所有文档。有时选出的标题具有误导性。
选择簇质心中一些具有较高权重的词项作为簇标签时,即使在差别式方法中它们不会被选出用作区分词项,但是这些高权重词项(或者短语,特别是名词短语更佳)往往比一些标题更有代表意义。当然,用户理解一系列短语所花费的时间会比理解标题更多。
总之,选择何种方法生成簇标签还需要结合实际应用来选择。
矩阵分解及隐性语义索引
词项——文档矩阵及 SVD
给定 M × N M×N M×N 的词项—文档矩阵 C C C,对矩阵 C C C进行SVD分解。
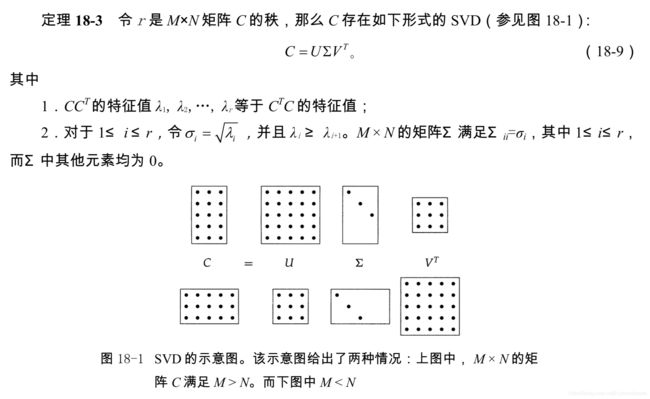
U U U 是一个 M × M M×M M×M 的矩阵,其每一列是矩阵 C C T CC^{T} CCT 的正交特征向量,而 N × N N×N N×N 矩阵 V V V 的每一列都是矩阵 C T C C^{T}C CTC 的正交特征向量。
注意到 C C T CC^{T} CCT矩阵中的第 i i i 行、第 j j j 列的元素实际上是第 i i i 个词项与第 j j j 个词项基于 文档共现次数 的一个重合度计算指标。
低秩逼近
给定 M × N M × N M×N 的矩阵及正整数 k k k,我们想寻找一个秩不高于 k k k的 M × N M × N M×N的矩阵 C k C_k Ck,使得两个矩阵的差 X = C − C k X = C − C_k X=C−Ck 的 F−范数(Frobenius Norm,弗罗宾尼其范数)最小,这是一个低秩逼近问题。
SVD 可以用于解决这样的低秩逼近问题,对于一个词项-文档矩阵的逼近问题,要进行如下三步操作:
(1) 给定 M × N M×N M×N 的词项—文档矩阵 C C C,按照公式(18-9)构造 SVD 分解,因此 C = U Σ V T C = UΣV^T C=UΣVT;
(2) 把 Σ Σ Σ 中对角线上 r − k r-k r−k 个最小奇异值置为 0,从而得到 Σ k Σ_k Σk;
(3) 计算 C k = U Σ k V T C_k = UΣ_kV^T Ck=UΣkVT 作为 C C C 的逼近。
实际上,上述过程产生了一个秩为 k k k 的矩阵,它的 F−范数误差最小。
LSI
在上一段介绍的词项-文档矩阵低秩逼近下能够为文档集中的每篇文档产生一个新的表示。同样,查询也可以映射到这个低秩表示空间,从而可以基于新的表示来进行查询和文档的相似度计算。这个过程被称为LSI。
引入LSI是为了试图解决一义多词(synonymy)和一词多义(polysemy)问题。那么能否利用词项的共现情况(比如,charge 是和 steed 还是 electron 在某篇文档中共现),来获得词项的隐性语义关联从而减轻这些问题的影响?
在 LSI 中,我们使用 SVD 分解来构造 C C C 的一个低秩逼近 C k C_k Ck,其中 k k k 取值往往在几百以内。这样,我们就可以将词项—文档矩阵中每行和每列(分别对应每个词项和每篇文档)映射到一个 k k k 维空间, C C T CC^T CCT 和 C T C C^TC CTC 的 k 个主特征向量可以定义该空间 。向量 q q q 可以通过下式变换到 LSI 空间:
q k → = Σ k − 1 U k T q → \overrightarrow {q_k}=\Sigma ^{-1}_{k}U^{T}_{k}\overrightarrow {q} qk=Σk−1UkTq
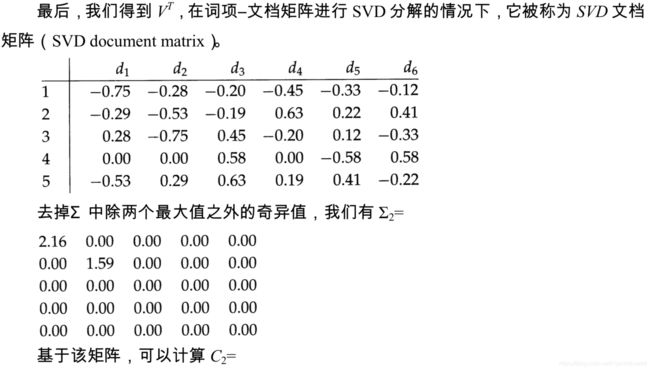
具体例子如下:
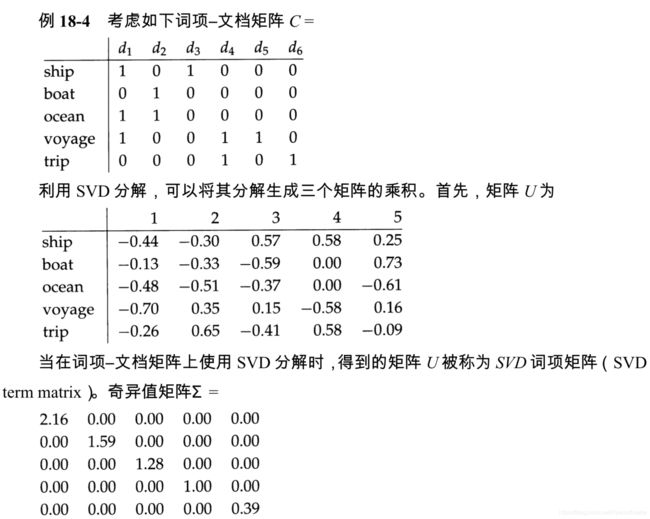
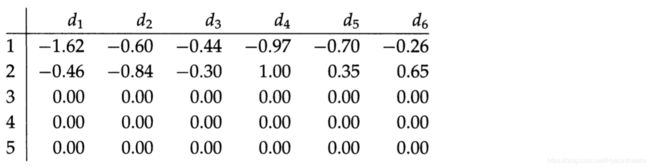
此时,截断 SVD 分解中的文档矩阵 ( V ′ ) T (V')^T (V′)T如下,这样的向量表示更加密集。

当将词项/文档表示到 k k k 维空间时,SVD 应该将共现上相似的词项合在一起。这个直觉也意味着,检索的质量不仅不太会受降维的影响,而且实际上有可能会提高。
在实验中得到的一些普遍结论有:
- SVD 的计算开销很大,成功分解超过一百万篇文档的矩阵是困难的。这也是一个阻碍 LSI 推广的主要障碍。
- 如果减低 k 值,那么如预期一样,召回率将会提高。
- 当 k 取几百之内的数目时,某些查询的正确率实际上也会得到提高。这也意味着,对于合适的 k 值,LSI 能部分解决一义多词的问题。
- 当查询和文档的重合度很低时,LSI 的效果最好。