用随机森林模型替代常用的回归和分类模型
随机森林模型有着惊人的准确性,可以替代一般线性模型(线性回归、方差分析等)和广义线性模型(逻辑斯蒂回归、泊松回归等)等等。
我2012年在人民大学组织的R语言会议上介绍了随机森林的用法(报告文件在http://cos.name/wp-content/uploads/2012/05/17-lixinhai-random-forest.pdf)。以后不时有人给我写信交流模型使用心得,索要数据和代码。我感觉当时的介绍不太充分。正巧《应用昆虫学报》的主编戈峰老师邀我写一篇统计方法的稿件,我便把随机森林的基本原理和应用案例重新细化,形成一篇文章(http://www.ent-bull.com.cn/viewmulu.aspx?qi_id=1031&mid=31191&xuhao=42)。文章的R语言代码显示效果不好(没有颜色,断行多),我便把文章和代码放到这个博客上。
文章正文(引用:李欣海. 2013. 随机森林模型在分类与回归分析中的应用. 应用昆虫学报, 50, 1190-1197)
前言
随机森林(Random Forest)是一种基于分类树(classification tree)的算法(Breiman,2001)。这个算法需要模拟和迭代,被归类为机器学习中的一种方法。经典的机器学习模型是神经网络(Hopfield,1982),有半个多世纪的历史了。神经网络预测精确,但是计算量很大。上世纪八十年代Breiman等人发明了分类和回归树(Classification and Regression Tree
简称CART)的算法(Breimanet al.,1984),通过反复二分数据进行分类或回归,计算量大大降低。2001年Breiman和Cutler借鉴贝尔实验室的Ho所提出的随机决策森林(random decision forests)(Ho,1995,1998)的方法,把分类树组合成随机森林(Breiman,2001),即在变量(列)的使用和数据(行)的使用上进行随机化,生成很多分类树,再汇总分类树的结果。后来Breiman在机器学习杂志上发表了他和Cutler设计的随机森林的算法(Breiman,2001)。这篇文章被大量引用(根据Google Scholar,该文章至2013年被引用9000多次),成为机器学习领域的一个里程碑。
随机森林在运算量没有显著提高的前提下提高了预测精度。随机森林对多元公线性不敏感,结果对缺失数据和非平衡的数据比较稳健,可以很好地预测多达几千个解释变量的作用(Breiman,2001),被誉为当前最好的算法之一(Iverson et al.,2008)。在机器学习的诸多算法中,随机森林因高效而准确而备受关注,在各行各业得到越来越多的应用(e.g Cutler et al.,2007;Genueret al.,2010)。
随机森林的算法最初以FORTRUN语言编码(Liaw,2012)。现在可以通过R语言或SAS等工具实现。R语言是一种用于统计分析和绘图的语言和操作环境(R Development Core Team,2013)。它是自由、免费、源代码开放的软件,近年来已经成为国际学术领域应用最广的统计工具。在国内,R语言也在迅速普及。本文基于R语言介绍随机森林的应用。R语言中有两个软件包可以运行随机森林,分别是randomForest(Liaw,2012)和party。本文介绍randomForest的用法。
本文面向没有或只有初步R语言基础的生态学工作者,以三个案例,通过运行案例中给出的R语言代码,读者可以运行随机森林的算法,进行分类或回归分析,得到变量的重要性、模型的误差等指标,并可以进行预测。Breiman发表随机森林后,有若干文章深入探讨其算法(Biau,2012),变量的比较(Archer and Kirnes,2008;Groemping,2009)和变量间的交互作用(Winham et al.,2012)等。本文旨在介绍随机森林的应用方法,不涉及其本身的算法,也不涉及同其他平行方法的比较。
1 随机森林的原理
同其他模型一样,随机森林可以解释若干自变量(X1、X2、...、Xk)对因变量Y的作用。如果因变量Y有n个观测值,有k个自变量与之相关;在构建分类树的时候,随机森林会随机地在原数据中重新选择n个观测值,其中有的观测值被选择多次,有的没有被选到,这是Bootstrap重新抽样的方法。同时,随机森林随机地从k个自变量选择部分变量进行分类树节点的确定。这样,每次构建的分类树都可能不一样。一般情况下,随机森林随机地生成几百个至几千个分类树,然后选择重复程度最高的树作为最终结果(Breiman,2001)。
2 随机森林的应用
随机森林可以用于分类和回归。当因变量Y是分类变量时,是分类;当因变量Y是连续变量时,是回归。自变量X可以是多个连续变量和多个分类变量的混合。在下面3个案例中,判别分析和对有无数据的分析是分类问题,对连续变量Y的解释是回归问题。
2.1 在判别分析中的应用
判别分析(discriminant analysis)是在因变量Y的几个分类水平明确的条件下,根据若干自变量判别每个观测值的类型归属问题的一种多变量统计分析方法。判别与分类在统计学概念上有所交叉,在本文中不强调两者的区别。案例1中有3种昆虫(A、B和C)形态接近,不过可以通过4个长度指标(L1、L2、L3和L4)进行种类的识别。具体数据如表1。
表1 3种昆虫及其用于分类的4个量度指标
Table 1 The four length indices for classifying threeinsect species
| 物种Species |
量度(Length) |
|||
| L1 |
L2 |
L3 |
L4 |
|
| A |
16 |
27 |
31 |
33 |
| A |
15 |
23 |
30 |
30 |
| A |
16 |
27 |
27 |
26 |
| A |
18 |
20 |
25 |
23 |
| A |
15 |
15 |
31 |
32 |
| A |
15 |
32 |
32 |
15 |
| A |
12 |
15 |
16 |
31 |
| B |
8 |
23 |
23 |
11 |
| B |
7 |
24 |
25 |
12 |
| B |
6 |
25 |
23 |
10 |
| B |
8 |
45 |
24 |
15 |
| B |
9 |
28 |
15 |
12 |
| B |
5 |
32 |
31 |
11 |
| C |
22 |
23 |
12 |
42 |
| C |
25 |
25 |
14 |
60 |
| C |
34 |
25 |
16 |
52 |
| C |
30 |
23 |
21 |
54 |
| C |
25 |
20 |
11 |
55 |
| C |
30 |
23 |
21 |
54 |
| C |
25 |
20 |
11 |
55 |
通过运行下列R语言代码,可以得到随机森林的结果RF1。R语言中的“#”表示注释,其后面的语句不被执行。当随机森林用于分类时,其结果RF1包含混淆矩阵(confusionmatrix)(表2),显示判别分析的错误率。
install.packages("randomForest") #安装随机森林程序包(每台计算机只需安装一次)
library(randomForest) #调用随机森林程序包(每次运行都要调用)
insect <- read.csv("d:/data/insects.csv", header = TRUE) #从硬盘读入数据到对象
insectRF1 <- randomForest(insect[,c('L1','L2','L3','L4')], insect[,'species'], importance=TRUE, ntree=10000) #运行随机森林模型
RF1 #显示模型结果,包括误差率和混淆矩阵(表2)
其中insect是一个包含5个变量20个记录的数据表。insect[,c('L1','L2','L3','L4')]表示昆虫的量度,是一个4乘以20的矩阵;insect[,'species']表示昆虫的物种类别,是20个物种名组成的一个向量。表2显示模型对A的判别错误率为28.6%,对B和C的判别错误率为0。
表2 随机森林(用于分类时)的混淆矩阵显示昆虫分类误差
Table2 Random Forest outputs a confusion matrix showing the classification error
| | A |
B |
C |
分类误差 Class error |
| A |
5 |
2 |
0 |
0.286 |
| B |
0 |
6 |
0 |
0 |
| C |
0 |
0 |
7 |
0 |
注:每行表示实际的类别,每列表示随机森林判定的类别。
The row indicates real classification;the column indicates predicted classification.
随机森林的结果内含判别函数,可以用下列代码根据新的量度判断昆虫的物种类别。
new.data <- data.frame(L1=20, L2=50, L3=30, L4=20) #一个新的昆虫的量度
predict(RF1, new.data, type="prob") #判别该量度的昆虫归类为A、B和C的概率
predict(RF1, new.data, type="response") #判别该量度的昆虫的类别
在该案例中,该量度判别为A、B和C的概率分别为82.4%、9.4%和8.2%。随机森林将其判别为A。
2.2 对有无数据的分析
对于有或无、生或死、发生或不发生等二分变量的分析,一般用逻辑斯蒂回归(logistic regression)的方法。逻辑斯蒂回归实质上是对因变量Y作两个分类水平的判别。逻辑斯蒂回归对自变量的多元共线性非常敏感,要求自变量之间相互独立。随机森林则完全不需要这个前提条件。Breiman在2001年发表了具有革命意义的文章,批判了当前主流的统计学方法,指出经典模型如逻辑斯蒂回归经常给出不可靠的结论,而随机森林准确而可靠。
案例2以朱鹮为例,说明该方法的具体应用。朱鹮的巢址选择受环境变量的影响(Li et al.,2006,2009;翟天庆和李欣海,2012)。假设朱鹮选择一个地方营巢的概率取决于下列自变量:土地利用类型(森林、草地、灌丛或农田等)、海拔、坡度、温度、降水、人类干扰指数等。该问题的因变量为朱鹮1981年至2008年间的532个巢(Y=1),以及在朱鹮巢区的系统选择的(等间距)2538个点(Y=0)(图3A);自变量为这3070个地点对应的8个环境变量。应用随机森林对朱鹮巢址选择进行分析的R语言代码如下:
ibis <- read.csv('d:/data/ibis.csv', header = TRUE) #从硬盘读入数据
ibis use<−as.factor(ibis use) # 定义巢址选择与否(0或1)为分类变量。这是因变量Y。
ibis landcover<−as.factor(ibis landcover) #定义土地利用类型为分类变量
RF2 <- randomForest(ibis[, c('elevation', 'footprint', 'GDP', 'landcover', 'pop', 'slope', 'prec_ann', 't_ann')],
ibis[,'use'], importance=TRUE, ntree=1000) #运行随机森林varImpPlot(RF2) #图示自变量对的巢址选择的重要性
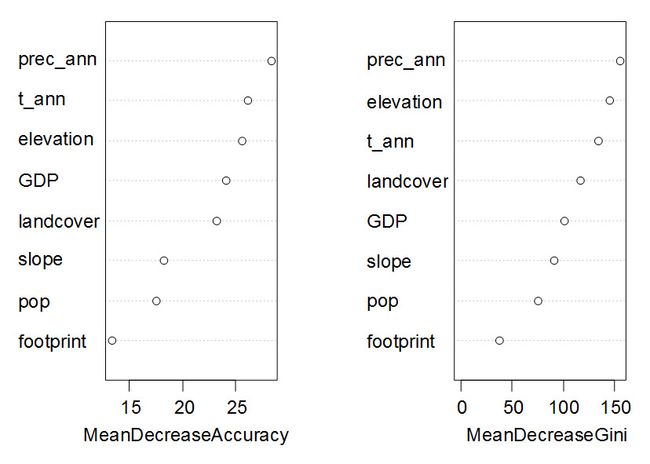
图1 随机森林对影响朱鹮巢址选择的自变量的重要性进行排序*
Fig. 1 Ranking variable importance thatassociated with nest site selection of the crested ibis by Random Forest*.
*MeanDecreaseAccuracy衡量把一个变量的取值变为随机数,随机森林预测准确性的降低程度。该值越大表示该变量的重要性越大[。MeanDecreaseGini通过基尼(Gini)指数计算每个变量对分类树每个节点上观测值的异质性的影响,从而比较变量的重要性。该值越大表示该变量的重要性越大。prec_ann是年总降水量;t_ann是年平均温度;elevation是海拔;GDP是国内生产总值;landcover是土地利用类型;slope是坡度;pop是人口密度;footprint是人类干扰指数。
从图1可以看到不同指标指示的变量重要性会略有差距,但是差距不会很大。
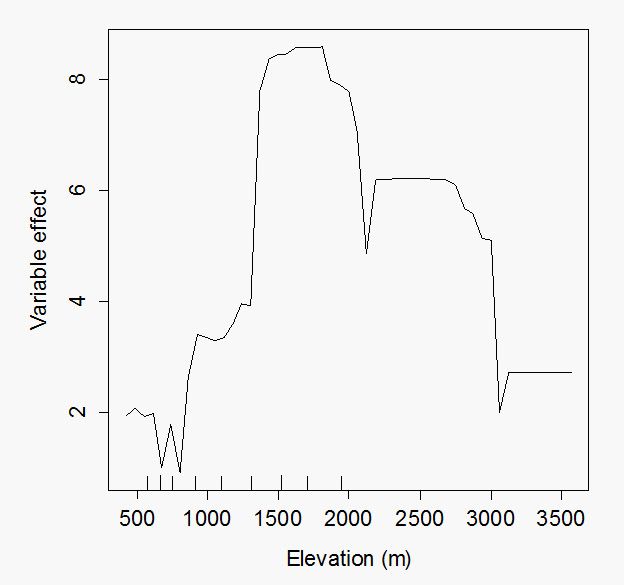
随机森林可以给出每个自变量对因变量的作用。下列R代码给出海拔对巢址选择的影响,结果在图2中,表示中等程度的海拔最适宜营巢。
partialPlot(RF2, ibis, elevation, "0", main='' , xlab='Elevation (m)', ylab="Variable effect")
图2 随机森林算出的海拔对朱鹮巢址选择的影响
Fig. 2 Partial effect of elevation onnest site selection of the crested ibis.
随机森林可以通过下列代码预测任何地点朱鹮营巢的概率(图3)
pred <- predict(RF2, ibis, type="prob")#计算原数据ibis中3070个地点被朱鹮选择营巢的概率
# 绘制图3A
plot(ibis x,ibis y, type = "n", xlab = '经度 Longitude', ylab = '纬度 Latitude') #绘制坐标轴
for (i in 1:length(ibis$x)){ #循环语句,从1到3070
if(ibis use[i]!=1)points(ibis x[i], ibis$y[i], col ="grey80", cex = .8, pch = 19) #非营巢点为灰色
if(ibis use[i]==1)points(ibis x[i], ibis$y[i], col = "black", cex = .8, pch = 19) #营巢点为黑色
}
#绘制图3B,颜色深的营巢概率高
plot(ibis x, ibis y, type = "n", xlab = '经度 Longitude', ylab = '纬度 Latitude') #绘制坐标轴
for (iin 1:length(ibis$x)){ #循环语句,从1到3070
图3 A朱鹮的巢址(黑色)和对照点(灰色);B随机森林算出的每个点朱鹮选择营巢的概率(深色概率高)
Fig.3 A. the nest site ofthe crested ibis (black dots) and the pseudo-absence points (grey dots); B. theprobability of nest site selection of the crested ibis calculated by RandomForest (dark color means higher probability)
2.3 回归分析
当因变量Y为连续变量时,随机森林通过一组自变量X对Y进行解释,类似经典的回归分析。
案例3依旧以朱鹮为例,介绍随机森林在回归分析上的应用。朱鹮是依赖湿地的鸟类,其生境可以分为一个个相邻的集水区。每个集水区内朱鹮的巢数同集水区的环境变量相关。用环境变量(包括连续变量和分类变量两个类型)解释集水区内朱鹮的巢数,可以被看作为一个回归的问题。下列代码读取数据并显示数据前6行:
sheds <- read.csv('d:/data/watersheds4.csv', header=T) #读取数据
head(sheds) #显示数据sheds的前6行,如表3所示。NA表示缺失值。
表3 朱鹮栖息地每个集水区内朱鹮的巢数以及环境变量
Table 3 The number of nests andenvironmental variables for every watershed in the habitat of the crested ibis
| Nests |
Elevation |
Footprint |
Temperature |
Rice_paddy |
Water_body |
Wetland |
Elev_SD |
| 1 |
597.83 |
44.54 |
14.02 |
0.14 |
0.52 |
0.07 |
197.54 |
| 0 |
588.74 |
32.41 |
14.09 |
0.15 |
0.08 |
0.01 |
148.32 |
| 0 |
513.84 |
NA |
14.66 |
0 |
0.16 |
0 |
28.84 |
| 5 |
609.33 |
30.2 |
14.29 |
1.17 |
1.03 |
1.21 |
184.58 |
| 0 |
NA |
35.88 |
13.32 |
0.18 |
0.17 |
0.03 |
NA |
| 2 |
651.08 |
47.62 |
14.41 |
1.11 |
0.34 |
0.38 |
121.37 |
对于缺失数据,R语言的randomForest软件包通过na.roughfix函数用中位数(对于连续变量)或众数(对于分类变量)来进行替换。
Dat.fill <- na.roughfix(sheds) #用中位数或众数替代缺失值
RF3 <-randomForest(Nests ~ Elevation + Footprint + Temperature + Rice_paddy +Water_body + Wetland + Elev_SD, data=Dat.fill,
ntree=5000, importance=TRUE,na.action=na.roughfix, mtry=3) #运行随机森林
RF3 #模型结果,显示残差的平方,以及解释变异(环境变量X对巢数Y的解释)的百分率
mtry指定分类树每个节点用来二分数据的自变量的个数。如果mtry没有被指定,随机森林用缺省值。对于分类(判别)分析(Y是分类变量),缺省值是自变量总数的平方根;如果是回归分析(Y是连续变量),缺省值是自变量总数的1/3。
3 讨论
本文以三个案例介绍了随机森林的具体应用。随机森林结构比较复杂,但是它却极端易用,需要的假设条件(如变量的独立性、正态性等)比逻辑斯蒂回归等模型要少得多。它也不需要检查变量的交互作用和非线性作用是否显著。在大多数情况下模型参数的缺省设置可以给出最优或接近最优的结果。使用者可以调节mtry的取值来检查模型的缺省值受否给出误差最小的结果。使用者也可以指定所用的分类树的数量。在计算负荷可以接受的情况下分类树的数量越大越好。图4可以帮助使用者判断最小的分类树的数量,以便节省计算时间。
目前,人们已经对多种机器学习的模型进行了比较(e.g. Li and Wang,2013;Kampichler et al.,2010),随机森林经常独占鳌头(Kampichler et al.,2010;Li et al.,2012)。随机森林通过产生大量的分类树,建立若干自
变量X和一个因变量Y的关系。随机森林的优点是:它的学习过程很快。在处理很大的数据时,它依旧非常高效。随机森林可以处理大量的多达几千个的自变量(Breiman,2001)。现有的随机森林算法评估所有变量的重要性,而不需要顾虑一般回归问题面临的多元共线性的问题。它包含估计缺失值的算法,如果有一部分的资料遗失,仍可以维持一定的准确度。随机森林中分类树的算法自然地包括了变量的交互作用(interaction)(Cutler, et al.,2007),即X1的变化导致X2对Y的作用发生改变。交互作用在其他模型中(如逻辑斯蒂回归)因其复杂性经常被忽略。随机森林对离群值不敏感,在随机干扰较多的情况下表现稳健。随机森林不易产生对数据的过度拟合(overfit)(Breiman,2001),然而这点尚有争议(Elith and Graham,2009)。
随机森林通过袋外误差(out-of-bag error)估计模型的误差。对于分类问题,误差是分类的错误率;对于回归问题,误差是残差的方差。随机森林的每棵分类树,都是对原始记录进行有放回的重抽样后生成的。每次重抽样大约1/3的记录没有被抽取(Liaw,2012)。没有被抽取的自然形成一个对照数据集。所以随机森林不需要另外预留部分数据做交叉验证,其本身的算法类似交叉验证,而且袋外误差是对预测误差的无偏估计(Breiman,2001)。
随机森林的缺点是它的算法倾向于观测值较多的类别(如果昆虫B的记录较多,而且昆虫A、B和C间的差距不大,预测值会倾向于B)。另外,随机森林中水平较多的分类属性的自变量(如土地利用类型 > 20个类别)比水平较少的分类属性的自变量(气候区类型<10个类别)对模型的影响大(Deng et al.,2011)。总之,随机森林功能强大而又简单易用,相信它会对各行各业的数据分析产生积极的推动作用。
参考文献
Breiman L. 2001. Random forests. Machine Learning, 45, 5-32
Hopfield JJ. 1982. Neural networks and physical systems withemergent collective computational abilities. Proceedings of the NationalAcademy of Sciences of the United States of America-Biological Sciences, 79,2554-2558
Breiman L, Friedman JH, Olshen RA, Stone CJ. 1984. Classificationand Regression Trees. Chapman and Hall.
Ho TK. 1995. Random Decision Forest. in Proceedings of the 3rdInternational Conference on Document Analysis and Recognition. 278-282.
Ho TK. 1998. The random subspace method for constructing decisionforests. in IEEE Transactions on Pattern Analysis and Machine Intelligence.832-844.
Breiman L. 2001. Statistical modeling: The two cultures.Statistical Science, 16, 199-215
Iverson LR, Prasad AM, Matthews SN, Peters M. 2008. Estimatingpotential habitat for 134 eastern US tree species under six climate scenarios.Forest Ecology and Management, 254, 390-406
Cutler DR, Edwards TC, Jr., Beard KH, Cutler A, Hess KT. 2007.Random forests for classification in ecology. Ecology, 88, 2783-2792
Genuer R, Poggi JM, Tuleau-Malot C. 2010. Variable selection usingrandom forests. Pattern Recognition Letters, 31, 2225-2236
Liaw A.2012. Package "randomForest".
R Development Core Team. 2013. R: A Language and Environment forStatistical Computing. R Foundation for Statistical Computing.
Biau G. 2012. Analysis of a random forests model. Journal ofMachine Learning Research, 13, 1063-1095
Archer KJ, Kirnes RV. 2008. Empirical characterization of randomforest variable importance measures. Computational Statistics & DataAnalysis, 52, 2249-2260
Groemping U. 2009. Variable importance assessment in regression:linear regression versus random forest. American Statistician, 63, 308-319
Winham S, Wang X, de Andrade M, Freimuth R, Colby C, Huebner M, BiernackaJ. 2012. Interaction detection with random forests in high-dimensional data.Genetic Epidemiology, 36, 142-142
Hosmer Jr DW, Lemeshow S. 1989. Applied Logistic Regression. JohnWiley & Sons.
Li XH, Tian HD, Li DM. 2009. Why the crested ibis declined in themiddle twentieth century. Biodiversity and Conservation, 18, 2165-2172
Li XH, Li DM, Ma ZJ, Schneider DC. 2006. Nest site use by crestedibis: dependence of a multifactor model on spatial scale. Landscape Ecology,21, 1207-1216
Zhai TQ (翟天庆),Li XH (李欣海). 2012. Climate change induced potential range shift of thecrested ibis based on ensemble models. Acta Ecologica Sinica (生态学报), 32, 2361-2370 (in Chinese)
Li XH, Wang Y. 2013. Applying various algorithms for speciesdistribution modeling. Integrative Zoology, 8, 124-135
Kampichler C, Wieland R, Calmé S, Weissenberger H, Arriaga-WeissS. 2010. Classification in conservation biology: A comparison of five machine-learningmethods. Ecological Informatics, 5, 441-450
Li XH, Tian HD, Li RQ, Song ZM, Zhang FC, Xu M, Li DM. 2012.Vulnerability of 208 endemic or endangered species in China to the effects ofclimate change Regional Environmental Change, DOI: 10.1007/s10113-10012-10344-z
Elith J, Graham CH. 2009. Do they? How do they? Why do theydiffer? On finding reasons for differing performances of species distributionmodels. Ecography, 32, 66-77
Deng H, Runger G, Tuv E. 2011. Bias of importance measures formulti-valued attributes and solutions. in Proceedings of the 21st InternationalConference on Artificial Neural Networks (ICANN).