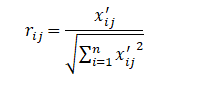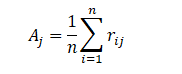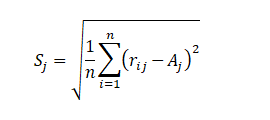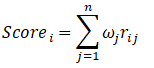权重计算方法三:变异系数法(Coefficient of Variation)
目录
1.原理简介
2.步骤详解
2.1 原始数据收集
2.2 指标数据正向化
2.3 数据标准化(消除量纲)
2.4 计算变异系数
2.5 计算权重及得分
3.案例分析
3.1 获取原始数据
3.2 指标正向化
3.3 数据标准化
3.4 计算变异系数
3.5 计算权重
4.完整代码(Java)
4.1 方法类CoV.java
4.2 主类CoVmain.java
1.原理简介
变异系数法是根据统计学方法计算得出系统各指标变化程度的方法,是直接利用各项指标所包含的信息,通过计算得到指标的权重,因此是一种客观赋权的方法。
变异系数法根据各评价指标当前值与目标值的变异程度来对各指标进行赋权,若某项指标的数值差异较大,能明确区分开各被评价对象,说明该指标的分辨信息丰富,因而应给该指标以较大的权重;反之,若各个被评价对象在某项指标上的数值差异较小,那么这项指标区分各评价对象的能力较弱,因而应给该指标较小的权重。
2.步骤详解
2.1 原始数据收集
假设一组数据中有m个指标,n条待评价样本,即一个n*m的矩阵,令其为X。其中xij表示第i行第j列的数据。
2.2 指标数据正向化
指标正向化的目的就是把所有的指标都转换为正向指标。
正向指标:又叫越大越优型指标,即该指标下的数据数值越大越好,例如成绩。
负向指标:又叫越小越优型指标,即该指标下的数据数值越小越好,例如排名。
对于正向指标:保持其原数据不变。
对于负向指标:采用如下方法。
其中k为指定的任意系数,其值可为0.1,0.2等; max|xj|表示第 j 列数据(指标)绝对值的最大值。
2.3 数据标准化(消除量纲)
由于不同的指标数据的单位不同,因此无法直接对其进行计算,而数据标准化的目的就是消除单位的影响,使所有数据都能够用同一种方法对其进行计算。令标准化后的数据矩阵为R.
2.4 计算变异系数
计算每个指标的均值:
计算每个指标的标准差(均方差):
因为标准差可以描述取值的离散程度,即某指标的方差反映了该指标的的分辨能力, 所以可用标准差定义指标的权重。
计算每个指标的变异系数:
2.5 计算权重及得分
权重:
得分:
3.案例分析
假设有以下数据,x1~x7为指标,ABC为三条待评价对象,其中x1和x4为负向指标,其余为正向指标。
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| A | 0.743 | 0.8267 | 0.8324 | 12 | 0.8637 | 0.0743 | 0.0409 |
| B | 0.7567 | 0.8033 | 0.8736 | -10 | 0.8538 | -0.0665 | 0.0716 |
| C | 0.8104 | 0.7667 | 0.8539 | 16 | 0.9038 | 0.0881 | 0.0657 |
3.1 获取原始数据
这里采用jxl包读取Excel。
//读取数据
public double[][] read(String filepath) throws IOException, BiffException,WriteException {
//创建输入流
InputStream stream = new FileInputStream(filepath);
//获取Excel文件对象
Workbook rwb = Workbook.getWorkbook(stream);
//获取文件的指定工作表 默认的第一个
Sheet sheet = rwb.getSheet("Sheet1");
rows = sheet.getRows();
cols = sheet.getColumns();
orig = new double[rows][cols];
pos = new double[rows][cols];
stand = new double[rows][cols];
//row为行
for(int i=0;i输出:
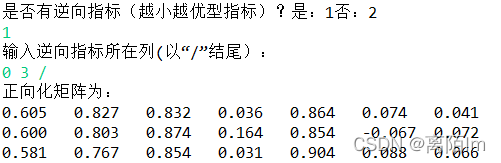
3.2 指标正向化
在此只需要对负向指标进行处理,正向指标保持原数据不变。
//指标正向化
public double[][] positive(double[][] or){
double k=0.1;
pos=or;
List neg=new ArrayList();//存储逆向指标所在列
System.out.println("是否有逆向指标(越小越优型指标)?是:1否:2");
int a=input.nextInt();
double[] max=getMax(or);
if(a==1) {
System.out.println("输入逆向指标所在列(以“/”结尾):");
while(!input.hasNext("/")) {
neg.add(Integer.valueOf(input.nextInt()));
}
for(int i=0;i 输出:
3.3 数据标准化
//数据标准化
public double[][] standar(double[][] p){
double[] sum=new double[p[0].length];
for(int i=0;i输出;
3.4 计算变异系数
//均值
double[] sum=new double[st[0].length];
for(int j=0;j输出:
3.5 计算权重
//各指标权重
double sumv=0;
for(int j=0;j输出:
4.完整代码(Java)
4.1 方法类CoV.java
/*
* 假设有m个方案,n个指标,憨憨为方案,列为指标
* 变异系数法(Coefficient of variation method)计算步骤
* 1.指标正向化:都转换为正向指标(越大越优型指标)
* 2.数据标准化:消除负数和量纲影响
* 3.计算变异系数:Aj(指标均值),Sj(指标标准差),则变异系数Vj=Sj/Aj
* 4.计算权重:Wj=Vj/sum(Vj)
*/
package CoV;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStream;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
import jxl.Cell;
import jxl.Sheet;
import jxl.Workbook;
import jxl.read.biff.BiffException;
import jxl.write.WriteException;
public class CoV {
private double[][] orig; //原始矩阵
private double[][] pos;//正向化矩阵
private double[][] stand;//标准化后的矩阵
int rows,cols;//存储Excel的行和列数
Scanner input = new Scanner(System.in);
//矩阵每列绝对值最大值
public double[] getMax(double[][] m) {
double max[] = new double[m[0].length];
for(int j=0;j < m[0].length;j++) {
max[j] = Math.abs(m[0][j]);
for(int i=0;i < m.length;i++) {
if(Math.abs(m[i][j]) >= max[j]) {
max[j] = Math.abs(m[i][j]);
}
}
}
return max;
}
//输出二维矩阵
public void matrixoutput(double[][] x) {
for(int i=0;i neg=new ArrayList();//存储逆向指标所在列
System.out.println("是否有逆向指标(越小越优型指标)?是:1否:2");
int a=input.nextInt();
double[] max=getMax(or);
if(a==1) {
System.out.println("输入逆向指标所在列(以“/”结尾):");
while(!input.hasNext("/")) {
neg.add(Integer.valueOf(input.nextInt()));
}
for(int i=0;i 4.2 主类CoVmain.java
package CoV;
import java.io.IOException;
import jxl.read.biff.BiffException;
import jxl.write.WriteException;
public class CoVmain {
public static void main(String args[]) throws BiffException, WriteException, IOException {
CoV cov=new CoV();
double[][] orig = cov.read("cov.xls");
//输出原始矩阵,行为评价对象,列为评价指标
System.out.println("原始矩阵为:");
cov.matrixoutput(orig);
double[][] pos = cov.positive(orig);
System.out.println("正向化矩阵为:");
cov.matrixoutput(pos);
double[][] stand = cov.standar(pos);
System.out.println("标准化矩阵为:");
cov.matrixoutput(stand);
double[][] W = cov.weigth(stand);
//输出每个指标的均值、标准差、变异系数和权重,依次按行排列
System.out.println("均值矩阵为:");
cov.matrixoutput1(W[0]);
System.out.println("标准差矩阵为:");
cov.matrixoutput1(W[1]);
System.out.println("变异系数矩阵为:");
cov.matrixoutput1(W[2]);
System.out.println("权重矩阵为:");
cov.matrixoutput1(W[3]);
}
}