强化学习的学习之路(十五)_2021-01-15: Sarsa和Q-learning及其Python实现
作为一个新手,写这个强化学习-基础知识专栏是想和大家分享一下自己学习强化学习的学习历程,希望对大家能有所帮助。这个系列后面会不断更新,希望自己在2021年能保证平均每日一更的更新速度,主要是介绍强化学习的基础知识,后面也会更新强化学习的论文阅读专栏。本来是想每一篇多更新一点内容的,后面发现大家上CSDN主要是来提问的,就把很多拆分开来了(而且这样每天任务量也小一点哈哈哈哈偷懒大法)。但是我还是希望知识点能成系统,所以我在目录里面都好按章节系统地写的,而且在github上写成了书籍的形式,如果大家觉得有帮助,希望从头看的话欢迎关注我的github啊,谢谢大家!另外我还会分享深度学习-基础知识专栏以及深度学习-论文阅读专栏,很早以前就和小伙伴们花了很多精力写的,如果有对深度学习感兴趣的小伙伴也欢迎大家关注啊。大家一起互相学习啊!可能会有很多错漏,希望大家批评指正!不要高估一年的努力,也不要低估十年的积累,与君共勉!
Sarsa和Q-learning及其Python实现
Sarsa
- An episode consists of an alternating sequence of states and state-action pairs:
- epsilon-greedy policy for one step, then bootstrap the action value function:
Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) ] Q\left(S_{t}, A_{t}\right) \leftarrow Q\left(S_{t}, A_{t}\right)+\alpha\left[R_{t+1}+\gamma Q\left(S_{t+1}, A_{t+1}\right)-Q\left(S_{t}, A_{t}\right)\right] Q(St,At)←Q(St,At)+α[Rt+1+γQ(St+1,At+1)−Q(St,At)]
The update is done after every transition from a nonterminal state S t TD target δ t = R t + 1 + γ Q ( S t + 1 , A t + 1 ) \begin{aligned} &\text { The update is done after every transition from a nonterminal state } S_{t}\\ &\text { TD target } \delta_{t}=R_{t+1}+\gamma Q\left(S_{t+1}, A_{t+1}\right) \end{aligned} The update is done after every transition from a nonterminal state St TD target δt=Rt+1+γQ(St+1,At+1)

Q-learning
We allow both behavior and target policies to improve
The target policy π \pi π is greedy on Q ( s , a ) Q(s, a) Q(s,a)
和SARSA不同的是,Q-learning采用不应的policy,这样收集数据的policy就可以有更多的探索。
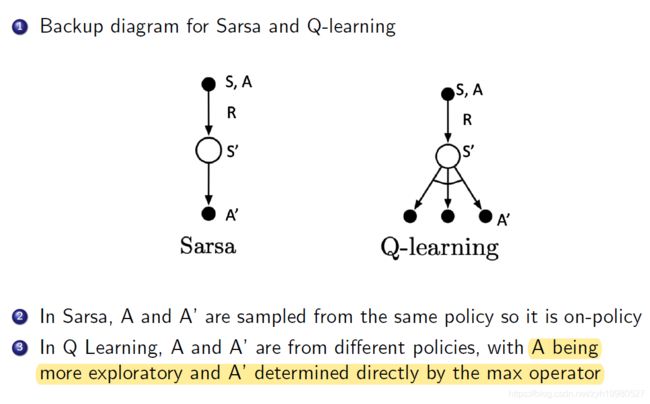
Q-learning和Sarsa的对比
on policy和off-policy
其实我觉得on-policy和off-policy之间差别就是看你优化的策略和你采数据的策略是不是同一个策略,如果是,那就是on-policy,如果不是,那就是off-policy。也就说off-policy有两个策略,一个是target policy,另一个是behavior policy。
off-policy 相对于on-policy会有一些好处:
- Learn about optimal policy while following exploratory policy
- Learn from observing humans or other agents
- Re-use experience generated from old policies π 1 , π 2 , … , π t − 1 \pi_{1}, \pi_{2}, \ldots, \pi_{t-1} π1,π2,…,πt−1
Importance sampling
重要性采样(Importance Sampling )是统计中的一种采样方法。在强化学习中经常用到这种采样方法,特别是off-policy方法当中,我们会用通过与环境交互的策略采集到的数据来去优化我们的策略。它主要用在一些难以直接采样的数据分布上。我们虽然无法从这个分布函数采样,但我们还有其他常见的、可以采样的分布,我们能不能对上面的公式进行一些变换,使用常见的分布采样呢?我们令待采样的分布为p(x ) ,另一个简单可采样且定义域与p(x)相同的概率密度函数为p(x) ,我们可以得到
E T ∼ π [ g ( T ) ] = ∫ P ( T ) g ( T ) d T = ∫ Q ( T ) P ( T ) Q ( T ) g ( T ) d T = E T ∼ μ [ P ( T ) Q ( T ) g ( T ) ] ≈ 1 n ∑ i P ( T i ) Q ( T i ) g ( T i ) \begin{aligned} \mathbb{E}_{T \sim \pi}[g(T)] &=\int P(T) g(T) d T \\ &=\int Q(T) \frac{P(T)}{Q(T)} g(T) d T \\ &=\mathbb{E}_{T \sim \mu}\left[\frac{P(T)}{Q(T)} g(T)\right] \\ & \approx \frac{1}{n} \sum_{i} \frac{P\left(T_{i}\right)}{Q\left(T_{i}\right)} g\left(T_{i}\right) \end{aligned} ET∼π[g(T)]=∫P(T)g(T)dT=∫Q(T)Q(T)P(T)g(T)dT=ET∼μ[Q(T)P(T)g(T)]≈n1i∑Q(Ti)P(Ti)g(Ti)
此时我们发现,公式变成了类似上一个方法的形式,而且我们只需要从这个简单 分布 p ~ ( x ) \tilde{p}(x) p~(x) 中采样,然后分别计算样本在两个分布中的概率和函数值,最后将三者组合起来就可以得到结果。选择一个合适的分布对重要性采样的重要d性: 要选择与原始分布尽可能接近的近似分布进行采样。如果选择不当,最终结果不会很好。
Why don’t use importance sampling on Q-Learning?
Q-learning is over the transition distribution, not over policy distribution thus no need to correct different policy distributions
Short answer: Because Q-learning does not make expected value estimates over the policy distribution. For the full answer click here
Q-learning及Sarsa的Python实现
这里我们主要是用Q-learning和Sarsa去解决Cliffwalk问题
# 作者:Yunhui
# 创建时间:2020/9/27 10:27
# IDE:PyCharm
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import hsv_to_rgb
def change_range(values, vmin=0, vmax=1):
"""
这个函数的作用是把values的值缩放到(vmin, vmax)之间,除数里面的1e-7是为了防止values里面都是0的时候造成分母为0
"""
start_zero = values - np.min(values)
return (start_zero / (np.max(start_zero) + 1e-7)) * (vmax - vmin) + vmin
class GridWorld:
# 这一块其实没懂地形的颜色是怎么用的
terrain_color = dict(normal=[127 / 360, 0, 96 / 100],
objective=[26 / 360, 100 / 100, 100 / 100],
cliff=[247 / 360, 92 / 100, 70 / 100],
player=[344 / 360, 93 / 100, 100 / 100])
def __init__(self):
self.player = None
self._create_grid()
self._draw_grid()
self.num_steps = 0
'''
(1)、以单下划线开头,表示这是一个保护成员,只有类对象和子类对象自己能访问到这些变量。以单下划线开头的变量和函数被默认当作是内部函数,
使用from module import *时不会被获取,但是使用import module可以获取
(2)、以单下划线结尾仅仅是为了区别该名称与关键词
(3)、双下划线开头,表示为私有成员,只允许类本身访问,子类也不行。在文本上被替换为_class__method
(4)、双下划线开头,双下划线结尾。一种约定,Python内部的名字,用来区别其他用户自定义的命名,以防冲突。是一些 Python 的“魔术”对象
,表示这是一个特殊成员,例如:定义类的时候,若是添加__init__方法,那么在创建类的实例的时候,实例会自动调用这个方法,一般用来对实
例的属性进行初使化,Python不建议将自己命名的方法写为这种形式。
'''
def _create_grid(self, initial_grid=None):
self.grid = self.terrain_color['normal'] * np.ones((4, 12, 3)) # 这里的(4,12)应该表示的是格子数,3表示的是RGB三个通道???
self._add_objectives(self.grid)
def _add_objectives(self, grid):
grid[-1, 1:11] = self.terrain_color['cliff'] # 整个Clifwalk的左上角是坐标(0,0),最下面一行的第1个到第10个格子是cliff陷阱
grid[-1, -1] = self.terrain_color['objective'] # 最下面一行的第11个格子是目标
def _draw_grid(self):
self.fig, self.ax = plt.subplots(figsize=(12, 4))
self.ax.grid(which='minor')
self.q_texts = [self.ax.text(*self._id_to_position(i)[::-1], '0',
fontsize=11, verticalalignment='center',
horizontalalignment='center') for i in range(12 * 4)]
self.im = self.ax.imshow(hsv_to_rgb(self.grid), cmap='terrain',
interpolation='nearest', vmin=0, vmax=1)
self.ax.set_xticks(np.arange(12))
self.ax.set_xticks(np.arange(12) - 0.5, minor=True)
self.ax.set_yticks(np.arange(4))
self.ax.set_yticks(np.arange(4) - 0.5, minor=True)
def reset(self): # 位置复原到坐标(3,0)
self.player = (3, 0)
self.num_steps = 0
return self._position_to_id(self.player)
# 下面的这两个函数是将二维坐标与一维数字进行相互转换,从左上角的0(0,0)到右下角的47(3,11),//表示除之后取整
def _position_to_id(self, pos):
""" Maps a position in x,y coordinates to a unique ID """
return pos[0] * 12 + pos[1]
def _id_to_position(self, idx):
return (idx // 12), (idx % 12)
# 动作0,1,2,3分别表示上、下、右、左,掉入cliff奖励为-100,结束;普通的格子奖励为-1,不结束;objective奖励为0,结束;
def step(self, action):
# Possible actions
if action == 0 and self.player[0] > 0:
self.player = (self.player[0] - 1, self.player[1])
if action == 1 and self.player[0] < 3:
self.player = (self.player[0] + 1, self.player[1])
if action == 2 and self.player[1] < 11:
self.player = (self.player[0], self.player[1] + 1)
if action == 3 and self.player[1] > 0:
self.player = (self.player[0], self.player[1] - 1)
self.num_steps = self.num_steps + 1
# Rules
if all(self.grid[self.player] == self.terrain_color['cliff']):
reward = -100
done = True
elif all(self.grid[self.player] == self.terrain_color['objective']):
reward = 0
done = True
else:
reward = -1
done = False
return self._position_to_id(self.player), reward, done
def render(self, q_values=None, action=None, max_q=False, colorize_q=False):
assert self.player is not None, 'You first need to call .reset()'
if colorize_q:
assert q_values is not None, 'q_values must not be None for using colorize_q'
grid = self.terrain_color['normal'] * np.ones((4, 12, 3))
values = change_range(np.max(q_values, -1)).reshape(4, 12)
grid[:, :, 1] = values
self._add_objectives(grid)
else:
grid = self.grid.copy()
grid[self.player] = self.terrain_color['player']
self.im.set_data(hsv_to_rgb(grid))
if q_values is not None:
xs = np.repeat(np.arange(12), 4)
ys = np.tile(np.arange(4), 12)
for i, text in enumerate(self.q_texts):
if max_q:
q = max(q_values[i])
txt = '{:.2f}'.format(q)
text.set_text(txt)
else:
actions = ['U', 'D', 'R', 'L']
txt = '\n'.join(['{}: {:.2f}'.format(k, q) for k, q in zip(actions, q_values[i])])
text.set_text(txt)
if action is not None:
self.ax.set_title(action, color='r', weight='bold', fontsize=32)
plt.pause(0.01)
def egreedy_policy(q_values, state, epsilon=0.1):
"""
Choose an action based on a epsilon greedy policy.
A random action is selected with epsilon probability, else select the best action.
"""
if np.random.random() < epsilon:
return np.random.choice(4)
else:
return np.argmax(q_values[state])
def q_learning(env, num_episodes=500, render=True, exploration=0.1, learning_rate=0.5, gamma=0.9):
q_values = np.zeros((num_states, num_actions))
ep_rewards = []
for i in range(num_episodes):
state = env.reset()
done = False
reward_sum = 0
while not done:
action = egreedy_policy(q_values, state, exploration)
next_state, reward, done = env.step(action)
reward_sum += reward
# 更新q表
td_target = reward + gamma * np.max(q_values[next_state])
td_error = td_target - q_values[state][action]
q_values[state][action] += learning_rate * td_error
state = next_state
if render:
env.render(q_values, action=actions[action], colorize_q=True)
if done:
print("第%d个epsiode已经结束" % i)
ep_rewards.append(reward_sum)
return ep_rewards, q_values
def sarsa(env, num_episodes=500, render=True, exploration_rate=0.1, learning_rate=0.5, gamma=0.9):
q_values_sarsa = np.zeros((num_states, num_actions))
ep_rewards = []
for _ in range(num_episodes):
state = env.reset()
done = False
reward_sum = 0
action = egreedy_policy(q_values_sarsa, state, exploration_rate) # 这里是和q_learning不一样的地方
while not done:
next_state, reward, done = env.step(action)
reward_sum += reward
# 选择动作
next_action = egreedy_policy(q_values_sarsa, next_state, exploration_rate)
td_target = reward + gamma * (q_values[next_state][next_action])
td_error = td_target - q_values_sarsa[state][action]
q_values_sarsa[state][action] += learning_rate * td_error
state = next_state
action = next_action
if render:
env.render(q_values, action=action[action], colorize=True)
ep_rewards.append(reward_sum)
return ep_rewards, q_values_sarsa
def play(q_values):
env = GridWorld()
state, done = env.reset()
while not done:
action = egreedy_policy(q_values, state, 0.0)
next_state, reward, done = env.step(action)
state = next_state
env.render(q_values=q_values, action=actions[action], colorize_q=True)
UP = 0
DOWN = 1
RIGHT = 2
LEFT = 3
actions = ['UP', 'DOWN', 'RIGHT', 'LEFT']
env = GridWorld()
num_states = 4 * 12 # The number of states in simply the number of "squares" in our grid world, in this case 4 * 12
num_actions = 4 # We have 4 possible actions, up, down, right and left
q_learning_rewards, q_values = q_learning(env, gamma=0.9, learning_rate=1, render=False)
print("q_learning_rewards:", q_learning_rewards)
print("q_values:", q_values)
env.render(q_values, colorize_q=True)
# 下面的这个zip其实相当于是要把10次试验的每个epsiode的reward取平均然后去画图,先得到的是一个10*5000的矩阵
q_learning_rewards, _ = zip(*[q_learning(env, render=True, exploration=0.1,
learning_rate=1) for _ in range(10)])
# 得到avg_reward其实就可以画图,就mean_reward主要是为了画平均reward的参考线以及打印出平均reward
avg_rewards = np.mean(q_learning_rewards, axis=0)
mean_reward = [np.mean(avg_rewards)] * len(avg_rewards)
fig, ax = plt.subplots()
ax.set_xlabel('Episodes using Q-learning')
ax.set_ylabel('Rewards')
ax.plot(avg_rewards)
ax.plot(mean_reward, 'g--')
print('Mean Reward using Q-Learning: {}'.format(mean_reward[0]))
# Sarsa learning for cliff walk
sarsa_rewards, q_values_sarsa = sarsa(env, render=False, learning_rate=0.5, gamma=0.99)
sarsa_rewards, _ = zip(*[sarsa(env, render=False, exploration_rate=0.2) for _ in range(10)])
avg_rewards = np.mean(sarsa_rewards, axis=0)
mean_reward = [np.mean(avg_rewards)] * len(avg_rewards)
fig, ax = plt.subplots()
ax.set_xlabel('Episodes using Sarsa')
ax.set_ylabel('Rewards')
ax.plot(avg_rewards)
ax.plot(mean_reward, 'g--')
print('Mean Reward using Sarsa: {}'.format(mean_reward[0]))
# visualize the episode in inference for Q-learing and Sarsa-learning
play(q_values)
play(q_values_sarsa)
Qlearning解决Frozenlake和Mountaincar的Python代码放在github上了。
上一篇:强化学习的学习之路(十四)_2021-01-14 :动态规划(DP)、蒙特卡罗(MC)、时间差分(TD)
下一篇:强化学习的学习之路(十六)_2021-01-16:价值函数近似(Value function approximation)