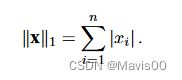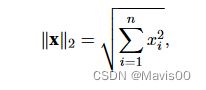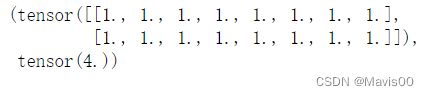《动手深度学习》2.3线性代数

基本运算

哈达玛积Hadamard product

指 两个矩阵的按元素乘法：数学符号⊙；
python运算：A*B

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()
A,B,A*B

降维&非降维

降维操作

• 降维的手段有很多，比如：求和A.sum(),求均值…
• 默认情况下，调用求和函数会沿所有的轴降低张量的维度，使它变为一个标量。
• 可以指定张量沿哪一 个轴来通过求和降低维度: A.sum(axis=0)表示对所有行求和，A.sum(axis=1)表示对所有列求和

A_sum_axis0 = A.sum(axis = 0)
A_sum_axis0, A_sum_axis0.shape

按axis = 0降维后，轴0消失，只剩下轴1的维数(即列数4)

A_sum_axis1 = A.sum(axis = 1)
A_sum_axis1, A_sum_axis1.shape

按axis = 1降维后，轴1消失，只剩下轴0的维数(即行数5)

• 平均值降维

A.mean(), A.sum() / A.numel()

• 对所有行求平均值降维，注意行数用A.shape[0]得到

A.mean(axis = 0),A.sum(axis = 0)/A.shape[0]

非降维求和，保持轴数不变

• 利用keepdims = True保持求和结果仍为二维矩阵，但是变成了5x1，列的dim变成了1

A.sum(axis=1, keepdims=True)

cumsum累加求和，各轴维度也不变

• cumsum函数：沿某个轴计算矩阵元素的累积总和，比如axis=0（按行计算累积和）。如此，不仅轴数不变，各轴的维度dim也保持不变。

A.cumsum(axis = 0)

乘法操作

点积

两种方法：

• torch.dot(x, y)

x = torch.arange(4, dtype=torch.float32) 
y = torch.ones(4, dtype=torch.float32)
x,y,torch.dot(x,y)

• 先执行按元素乘法，再求和来计算点积

torch.sum(x*y), (x*y).sum()

矩阵-向量乘法

• 前提：矩阵A的列数=向量x的维数
• python命令：torch.mv(A, x)
  

A.shape, x.shape, torch.mv(A, x)

矩阵-矩阵乘法

• 前提：A的列数 = B的行数
• python命令：torch.mm(A,B)
  

B = torch.ones(4, 3)
A.shape, B.shape, torch.mm(A, B)

向量范数 norm

L1范数

对各个元素的绝对值求和

u = torch.tensor([3.0, -4.0])
L1 = torch.abs(u).sum()
L1

L2范数，即默认的norm()函数

u = torch.tensor([3.0, -4.0])
L2 = torch.norm(u)
L2

Lp范数

矩阵范数——Frobenius范数

矩阵元素平方和的平方根，类似于向量的L2范数，直接用torch.norm(矩阵)。

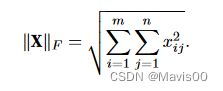
K = torch.ones((2, 8))
K, torch.norm(K)

范数和目标

在深度学习中，解决优化问题时，目标函数，通常被表达为范数。比如：

• 最大化分配给观测数据的概率;
• 最小化预测和真实观测之间的距离;
• 用向量表示物品（如单词、产品或新闻文章），以便最小化相似项目之间的距离，最大化不同项目之间 的距离。

2.3.13 练习

7.考虑一个具有形状(2, 3, 4)的张量，在轴0、1、2上的求和输出是什么形状?

• axis = 0

X = torch.randint(1,10,(2,3,4))
Y = torch.sum(X,axis = 0)
X,Y, Y.shape 

按第一个维度进行加法运算，运算后第一个维度被消除，得到3x4的矩阵

• axis = 1

X = torch.randint(1,10,(2,3,4))
Y = torch.sum(X,axis = 1)
X,Y, Y.shape 

对两个矩阵分别对所有行求和，每个矩阵被压缩为一个1x4的向量。
4+7+1=12,8+3+9=20,6+9+1=16,2+5+5=12
所以有行向量[12,20,16,12]

• axis = 2

Y = torch.sum(X,axis = 2,)
X,Y, Y.shape 

4+8+6+2=20；
7+3+9+5=24；
1+9+1+5=16；所以得到[20,24,16]

axis = 2且保持轴数不变的话：

8. 为linalg.norm函数提供3个或更多轴的张量，并观察其输出。对于任意形状的张量这个函数计算得到什么

X = torch.ones(2,3,6)
L2 = torch.norm(X)
X,L2