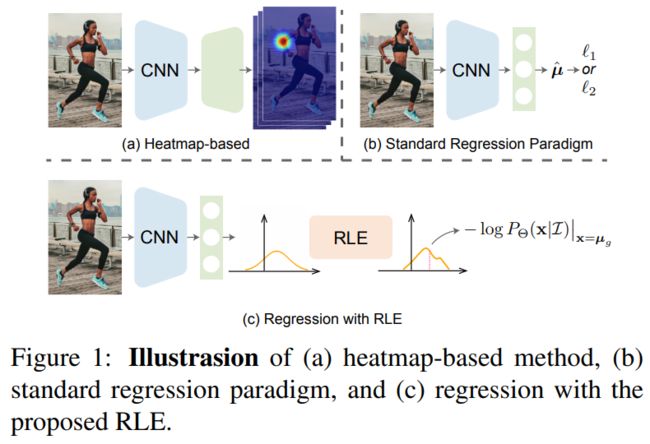
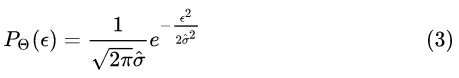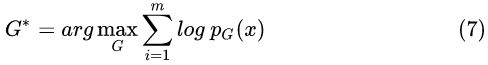姿态估计之2D人体姿态估计 - Human Pose Regression with Residual Log-likelihood Estimation(RLE)

【参考】重点看第四篇

2. 
   [ICCV2021 Oral] 学习潜在的误差分布——Human Pose Regression with Residual Log-likelihood Estimation(RLE) 论文笔记 - 知乎
3. RLE重铸回归方法的荣光后，回归和热图的异同究竟在何方？| 姿态估计ICCV2021 读后实验 - 知乎
4. 零基础看懂RLE（Residual Log-likelihood Estimation）|姿态估计ICCV 2021 Oral - 知乎
5. 基于流的生成模型-Flow based generative models - 知乎   李宏毅老师 笔记

将训练中的误差作为样本，利用MLE极大似然估计和 Flow-based 生成模型学习潜在的误差分布

这是ICCV2021 Oral的一篇论文，在跟进姿态估计的最新论文时偶然间看到的。论文的核心思想就是上方引用中的内容，虽然这篇论文针对的是人体姿态估计，但是其学习误差分布的思想可以扩展到任何任务。

工作的核心在于，通过flow方法，估计出模型输出关节的分布概率密度。一旦估计出令人满意的先验分布函数，就能动态优化损失函数loss，从而促进模型的回归训练。结果上讲，该论文也交出了一份令人满意的答卷：有史以来第一次，回归关节坐标的方法比高斯热图方法取得了更好的效果，而且，回归方法还能保持更快、更轻。

1. 从高斯热图说起

众所周知，姿态估计分为坐标回归和热图回归两派，我一开始接触的就是热图回归。而热图回归中的热图一直以来都使用手工设计  的二维独立高斯分布。例如假设输出热图  分辨率为64×64，则  为2，热图上某一位置  的值则为

 

其中  是该输入图片中该关键点的真实坐标点。

为什么使用高斯分布呢？直到看了这篇论文清楚了高斯分布热图的合理性。

2. 坐标误差分布

MSE "Mean Square Error" 

 便于理解，可以先从坐标回归的  损失函数看起。坐标回归直接预测特征点坐标  （有的也会同时预测  ，代表误差分布的方差），而  损失函数为：

                                                          (2)

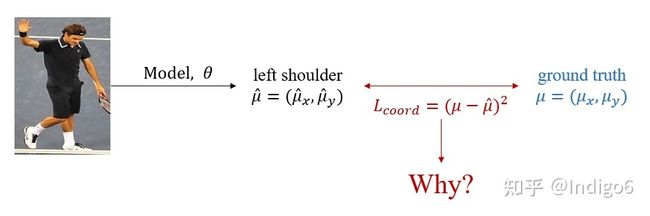
这里我们只先关注某一个关键点，如左肩膀。这个损失函数十分直观，即让预测的坐标点接近真实坐标点，它可以由极大似然估计推导出来。

2.1 极大似然估计

[极大似然估计(Maximum likelihood estimation)]

设样本服从正态分布，则似然函数为

  我们假设误差  符合期望为0、方差为  的高斯分布：

至于为什么可以这么假设，可以参见下面这个回答的最后部分，大致是中心极限定理。

最小二乘法的本质是什么？ - 马同学的回答 - 知乎  最小二乘法的本质是什么？ - 知乎

不同于最小二乘法的是，我们这里预测了 ，代表对于不同特征点/人体，误差分布的方差不同。

Output density

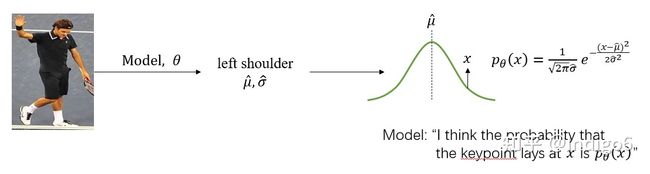
从另一个角度理解（原论文的角度），我们可以认为坐标回归预测了一个高斯分布，高斯分布的期望为  、方差为 ，即预测真实特征点的坐标在某一点X  的概率满足该分布：

  

 这里就解释了为什么热图回归中的热图采用高斯分布。而实际上我们观察到的样本为  ，那么采用极大似然估计法，我们则需要最大化  ：

 如果我们假设  是常数，就可以从 (5) 式得到 (1) 式。

2.2 真的是高斯分布吗？（论文的动机）

论文中提到之前有其它工作指出，使用拉普拉斯分布假设可以获得更好的性能，对应着  损失函数。一个更接近真实误差分布的分布假设，应该能够有更好的性能。因此作者提出使用 flow-based generativate model 来学习潜在的误差分布。

3. 核心思想

3.1 Flow-based generativate model

Flow-based generativate model，来源：李宏毅老师课件

首先简单介绍一下 Flow-based generativate model（以下简称Flow），其目标是训练一个生成器 G ，将一个简单分布  中的样本转换成复杂分布  中的样本：

对于复杂分布  我们观察到的样本是（比如动漫头像生成任务中真实动漫头像），因此根据极大似然估计，我们需要最大化这些样本出现的概率：

 

 而根据图片右上角的公式，可得：

 这里不需要清楚为什么，只需要知道生成器 G 被设计成很容易求逆函数  。整个训练过程就是将所有观察到的复杂分布的样本  求逆并最大化其概率。

接下来的问题就是将简单分布转换到怎样的复杂分布（变量是什么，  还是  等），这就引出原论文中的三种设计。
 

3.2 Basic Design

直接学习把预测的期望为 、方差为  的高斯分布转换到特征点坐标  的潜在分布，因此训练时以每一个  为观察到的样本。

Basic design

这种设计有什么问题呢？原文中写到：

Therefore, ϕ will learn to fit the distribution of   across all images. Nevertheless, the distribution that we want to learn is about how the output deviates from the ground truth conditioning on the input image, not the distribution of the ground truth itself across all images

个人认为这种设计不好的原因可能是几乎每一次训练的简单分布都不同，每个人体的每一个特征点坐标的复杂分布也都不同。某一个复杂分布刚利用一个样本训练了从这种简单分布到自己的映射，结果下一次又换了一个简单分布，训练样本被分散了。

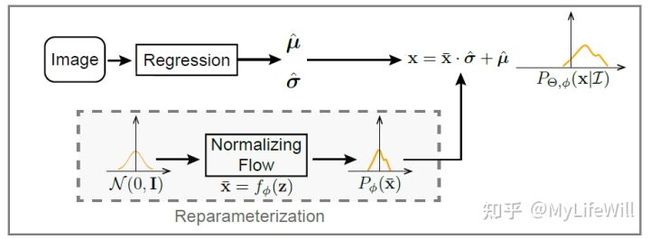
3.3 Reparameterization

学习把标准正态分布转换到误差  的潜在分布，相当于利用重参数化技巧巧妙地实现 Basic Design 的目标，同时避开了 Basic Design 中训练样本被分散的问题。

Direct likelihood estimation with reparameterization

这种设计相当于将训练过程中的所有误差作为样本，但是一开始坐标预测误差很大、Flow也刚开始训练，很可能Flow学到了错误的误差分布，而 Regressor 又采用了这种错误的误差分布（损失函数）作为指导，无法互相促进。

这种设计相当于将训练过程中的所有误差作为样本，但是一开始坐标预测误差很大、Flow也刚开始训练，很可能Flow学到了错误的误差分布，而 Regressor 又采用了这种错误的误差分布（损失函数）作为指导，无法互相促进。

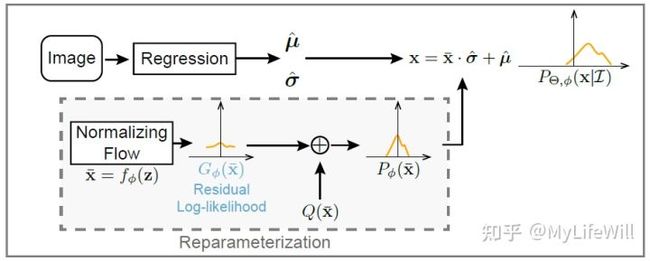
3.4 Residual Log-likelihood Estimation

学习把标准正态分布转换到误差  的潜在分布与高斯分布的商 (Residual)，主要是为了解决上一设计提到的冷启动问题（应该可以这么说？ ）。

Residual log-likelihood estimation with reparameterization

从损失函数角度来看，其实就是加入了手工设计的  损失函数项 ：

其中  是标准正态分布。

4. 其它

5. 参考资料：

1. 李宏毅老师的课程 Flow-based Generative Model
2. 基于流的生成模型-Flow based generative models - 知乎(文字版本)
3. 李宏毅-Flow-based Generative Model_哔哩哔哩_bilibili
4. 论文地址 https://arxiv.org/pdf/2107.11291.pdf
5. 代码地址 https://github.com/Jeff-sjtu/res-loglikelihood-regression