2021-Lite-HRNet: A Lightweight High-Resolution Network

1. Title

Lite-HRNet: A Lightweight High-Resolution Network

2. Summary

本文是想制作一个高性能的轻量化HRNet网络，我个人实际使用中会发现，Small HRNet的性能一般会比同量级的UNet要差一些，个人理解是多尺度信息交互不够充分的原因，毕竟原来的交互方式很简单（带步长的卷积进行下采样，双线性插值进行上采样），因此简单对HRNet进行放缩是不能取得较好的trade-off的。
作者首先是在HRNet中引入Shuffle Block，得到了Naive Lite-HRNet，并且在性能和复杂度上取得了不错的tradeoff。通过进一步分析，作者认为Shuffle Block中的1*1 Conv成为了性能瓶颈，因此想解决这个问题。
在HRNet中多个branch独立使用1*1 Conv计算复杂度会比较高，因此，作者想到了首先把多个branch的特征聚合起来，增强后，然后再作为权重分发回原branch，聚合过程中通过Pooling的方法降低feature map的大小，以此来降低整体计算复杂度，分发过程中再重新上采样回原始分辨率。这样一来一方面可以降低计算复杂度，另一方面还能将独立的各个分支的信息聚合起来，引入多尺度交互，以弥补spatial信息的损失。
个人认为，采用类似的思路，在HRNet多尺度特征交互方面再做些文章是可以进一步提升精度。

3. Problem Statement

Human pose estimation一般比较依赖于高分辨率的特征表示以获得较好的性能，但是目前的网络计算量较大，不能称之为一个高效的网络结构，因此，本文想解决的问题就是如何在计算资源受到约束的情况下部署一个高效的高分辨率模型。
通过简单地将ShuffleNet中的Shuffle Block应用于HRNet，即可得到一个轻量级的HRNet，并且可以获得超越MobileNet、ShuffleNet以及Small HRNet的性能，但是Shuffle Blocks中大量使用的1*1 Conv成为了计算瓶颈，因此，如何能替换掉成本较高的1*1 Conv并且保持甚至取得超越其性能是本文要解决的核心问题。

4. Method(s)

4.1 Naive Lite-HRNet

（1）Shuffle Blocks

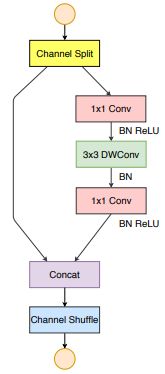
Shuffle Block会将通道首先分为两个部分，其中的一部分会送入一个1*1 Conv 3*3 DepthWise Conv和1*1 Conv中进行增强，处理完后会和另一部分拼接起来，最终会把通道重新shuffle。

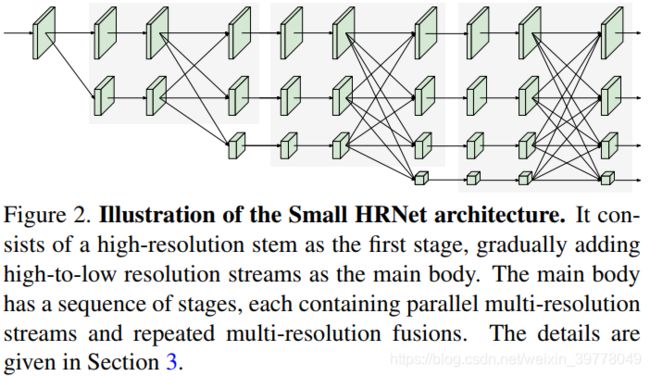
（2）HRNet

HRNet有两大优点：

1. 通过全程保持高分辨率的特征，有利于位置信息的保留，对于位置敏感的任务例如语义分割、目标检测、人体姿态估计等都具有良好的作用。
2. 另外通过充分地多尺度特征融合，HRNet有利于多尺度信息的挖掘，对于目标的尺度变化不敏感。

（3）Simple Combination

通过简单将Stem中的第2个3*3 Conv以及所有的Residual Block替换为Shuffle Block，并且将所有multi-resolution fusion中的Conv替换为Separable Conv，即可得到 Naive Lite-HRNet。
下面是官方代码中Stem的部分的实现，部分需要说明或者注意的地方，已经加上了中文注释：

class Stem(nn.Module):
    def __init__(self,
                 in_channels,
                 stem_channels,
                 out_channels,
                 expand_ratio,
                 conv_cfg=None,
                 norm_cfg=dict(type='BN'),
                 # 是否使用torch.utils.checkpoint用于降低显存使用，与模型实现没有关系，可以忽略
                 # 可参考博客：https://blog.csdn.net/ONE_SIX_MIX/article/details/93937091
                 with_cp=False):  
        super().__init__()
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.conv_cfg = conv_cfg
        self.norm_cfg = norm_cfg
        self.with_cp = with_cp
		
		# Stem中的第一个卷积不使用shuffle block
		# ConvModule是MMCV中的一个基本卷积模块：conv/norm/activation
        self.conv1 = ConvModule(
            in_channels=in_channels,
            out_channels=stem_channels,
            kernel_size=3,
            stride=2,
            padding=1,
            conv_cfg=self.conv_cfg,
            norm_cfg=self.norm_cfg,
            act_cfg=dict(type='ReLU'))
		
        mid_channels = int(round(stem_channels * expand_ratio))
        branch_channels = stem_channels // 2
        if stem_channels == self.out_channels:
            inc_channels = self.out_channels - branch_channels
        else:
            inc_channels = self.out_channels - stem_channels
		
		# Shuffle Block中左侧不做增强的分支
        self.branch1 = nn.Sequential(
            ConvModule(
                branch_channels,
                branch_channels,
                kernel_size=3,
                stride=2,
                padding=1,
                groups=branch_channels,
                conv_cfg=conv_cfg,
                norm_cfg=norm_cfg,
                act_cfg=None),
            ConvModule(
                branch_channels,
                inc_channels,
                kernel_size=1,
                stride=1,
                padding=0,
                conv_cfg=conv_cfg,
                norm_cfg=norm_cfg,
                act_cfg=dict(type='ReLU')),
        )
		
		# Shuffle Block中右侧增强分支
        self.expand_conv = ConvModule(
            branch_channels,
            mid_channels,
            kernel_size=1,
            stride=1,
            padding=0,
            conv_cfg=conv_cfg,
            norm_cfg=norm_cfg,
            act_cfg=dict(type='ReLU'))
        self.depthwise_conv = ConvModule(
            mid_channels,
            mid_channels,
            kernel_size=3,
            stride=2,
            padding=1,
            groups=mid_channels,  # groups=in_channels 深度可分离卷积
            conv_cfg=conv_cfg,
            norm_cfg=norm_cfg,
            act_cfg=None)
        self.linear_conv = ConvModule(
            mid_channels,
            branch_channels
            if stem_channels == self.out_channels else stem_channels,
            kernel_size=1,
            stride=1,
            padding=0,
            conv_cfg=conv_cfg,
            norm_cfg=norm_cfg,
            act_cfg=dict(type='ReLU'))

    def forward(self, x):

        def _inner_forward(x):
            x = self.conv1(x)
            x1, x2 = x.chunk(2, dim=1)

            x2 = self.expand_conv(x2)
            x2 = self.depthwise_conv(x2)
            x2 = self.linear_conv(x2)

            out = torch.cat((self.branch1(x1), x2), dim=1)

            out = channel_shuffle(out, 2)  # shuffle channel

            return out

        if self.with_cp and x.requires_grad:
            out = cp.checkpoint(_inner_forward, x)
        else:
            out = _inner_forward(x)

        return out

4.2 Lite-HRNet

（1）1*1 Convolution is Costly

1*1 Conv的计算复杂度为$\Theta \left(C^2\right)$，3*3 DepthWiseConv的计算复杂度为$\Theta (9C)$，其中C为通道数目，具体推导参见后文的5. Conclusion部分。
在Shuffle Block中，当$C>5$时，两个1*1卷积的计算复杂度就会超过一个depthwise conv的计算复杂度。

（2）Conditional Channel Weighting

为了降低计算复杂度，本文则是提出使用Element-wise weighting operation去代替1*1 Conv。
$${\mathrm{Y}}_s={\mathrm{W}}_s\odot {\mathrm{X}}_s$$
其中$W_s$是一个3d的tensor，大小为$W_s\ast H_s\ast C_s$，$\odot$是点乘符号。
比较不同的一点是，这个权重会从不同分辨率的feature map中计算得到，可以起到一个跨通道、跨分辨率的特征交互的作用。

（3）Cross-Resolution Weight Computation

对于第$s$个stage来说，其具有$s$个平行分支，每个分支的分辨率各不相同，相应地其也会有$s$个weight maps：$W_1,W_2,\dots ,W_s$。这$s$个weight map将由s个分辨率特征图计算而来：
$$\left({\mathrm{W}}_1,{\mathrm{W}}_2,\dots ,{\mathrm{W}}_s\right)={\mathcal{H}}_s\left({\mathrm{X}}_1,{\mathrm{X}}_2,\dots ,{\mathrm{X}}_s\right)$$
其中$\left\{{\mathrm{X}}_1,\dots ,{\mathrm{X}}_s\right\}$是$s$个不同resolution的输入，$X_1$表示最大的分辨率，$X_s$则是第$s$个分辨率feature map。
${\mathcal{H}}_s$操作具体为：
$$\begin{array}{rl}\left({\mathrm{X}}_1^{\prime },{\mathrm{X}}_2^{\prime },\dots ,{\mathrm{X}}_s\right)& \to \text{ Conv. }\to \mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}\to \text{ Conv. }\to \text{ sigmoid }\to \left({\mathrm{W}}_1^{\prime },{\mathrm{W}}_2^{\prime },\dots ,{\mathrm{W}}_s^{\prime }\right)\end{array}$$
其中${\mathrm{X}}_1^{\prime }=\mathrm{A}\mathrm{A}\mathrm{P}\left({\mathrm{X}}_1\right)$，AAP表示Adaptive Average Pooling，${\mathrm{X}}_i^{\prime }$维度均为$W_s\ast H_s$，实际上是对空间域进行了压缩。

这一部分对应的官方代码为：

class CrossResolutionWeighting(nn.Module):
    def __init__(self,
                 channels,
                 ratio=16,
                 conv_cfg=None,
                 norm_cfg=None,
                 act_cfg=(dict(type='ReLU'), dict(type='Sigmoid'))):
        super().__init__()
        if isinstance(act_cfg, dict):
            act_cfg = (act_cfg, act_cfg)
        assert len(act_cfg) == 2
        assert mmcv.is_tuple_of(act_cfg, dict)
        self.channels = channels
        total_channel = sum(channels)
        self.conv1 = ConvModule(
            in_channels=total_channel,
            out_channels=int(total_channel / ratio),
            kernel_size=1,
            stride=1,
            conv_cfg=conv_cfg,
            norm_cfg=norm_cfg,
            act_cfg=act_cfg[0])
        self.conv2 = ConvModule(
            in_channels=int(total_channel / ratio),
            out_channels=total_channel,
            kernel_size=1,
            stride=1,
            conv_cfg=conv_cfg,
            norm_cfg=norm_cfg,
            act_cfg=act_cfg[1])

    def forward(self, x):
    	# mini_size即为当前stage中最小分辨率的shape：H_s, W_s
        mini_size = x[-1].size()[-2:]  # H_s, W_s
        # 将所有stage的input均压缩至最小分辨率，由于最小的一个stage的分辨率已经是最小的了
        # 因此不需要进行压缩
        out = [F.adaptive_avg_pool2d(s, mini_size) for s in x[:-1]] + [x[-1]]
        out = torch.cat(out, dim=1)
        out = self.conv1(out)  # ReLu激活
        out = self.conv2(out)  # sigmoid激活
        out = torch.split(out, self.channels, dim=1)
        out = [
        	# s为原输入
        	# a为权重，并通过最近邻插值还原回原输入尺度
            s * F.interpolate(a, size=s.size()[-2:], mode='nearest')
            for s, a in zip(x, out)
        ]
        return out

（4）Spatial Weight Computation

在引入跨分辨率信息后，本文还引入了一个单分辨率内部空间域的增强操作：
$${\mathbf{w}}_s={\mathcal{F}}_s\left({\mathrm{X}}_s\right)$$
其中${\mathcal{F}}_s(\cdot )$的具体实现为：
$$\begin{array}{r}{\mathrm{X}}_s\to \mathrm{G}\mathrm{A}\mathrm{P}\to \mathrm{F}\mathrm{C}\to \mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}\to \mathrm{F}\mathrm{C}\to \text{ sigmoid }\to {\mathrm{w}}_s\end{array}$$
官方代码中的具体实现为：

class SpatialWeighting(nn.Module):
    def __init__(self,
                 channels,
                 ratio=16,
                 conv_cfg=None,
                 act_cfg=(dict(type='ReLU'), dict(type='Sigmoid'))):
        super().__init__()
        if isinstance(act_cfg, dict):
            act_cfg = (act_cfg, act_cfg)
        assert len(act_cfg) == 2
        assert mmcv.is_tuple_of(act_cfg, dict)
        self.global_avgpool = nn.AdaptiveAvgPool2d(1)
        self.conv1 = ConvModule(
            in_channels=channels,
            out_channels=int(channels / ratio),
            kernel_size=1,
            stride=1,
            conv_cfg=conv_cfg,
            act_cfg=act_cfg[0])
        self.conv2 = ConvModule(
            in_channels=int(channels / ratio),
            out_channels=channels,
            kernel_size=1,
            stride=1,
            conv_cfg=conv_cfg,
            act_cfg=act_cfg[1])

    def forward(self, x):
        out = self.global_avgpool(x)
        out = self.conv1(out)
        out = self.conv2(out)
        return x * out

（5）Instantiation

5. Evaluation

（1）计算复杂度对比

首先作者给出了各个操作的计算复杂度对比：

具体推导可参加下图：

其复杂度的降低主要来源于两个Pooling的操作，将空间尺度压缩了很多。

（2）Pose Estimation

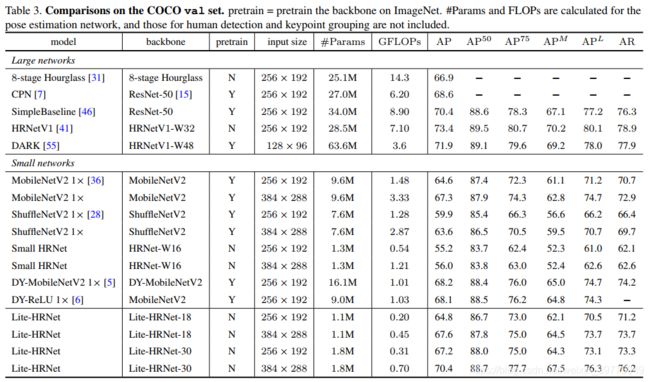
可以看出，效果还是很不错的，在一众小网络中取得了不错的精度平衡。

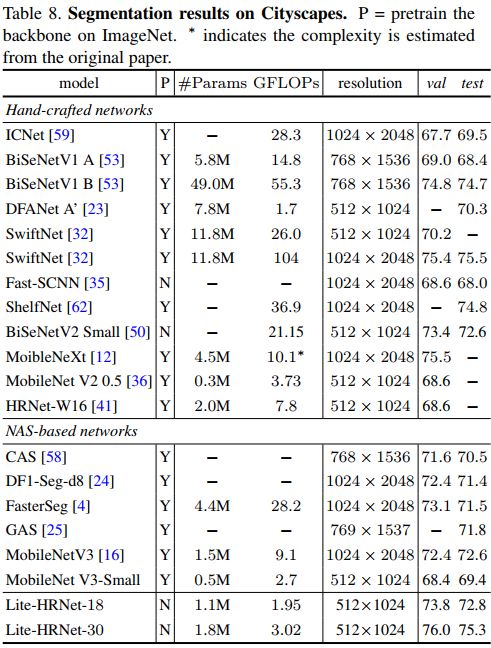
（3）Semantic Segmentation

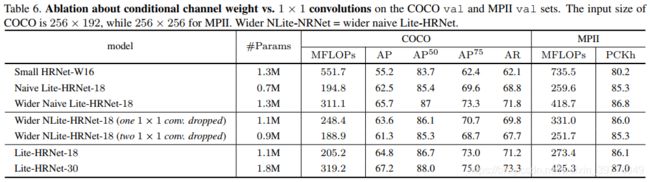
（4）消融实验

6. Conclusion

本文主要是在做一个高分辨率的轻量化网络，将Shuffle Block迁移进来，并且基于HRNet多尺度信息丰富的特性，加入了多尺度信息交互，并通过pooling的方法，降低了计算复杂度，同时也获得了较好的性能。