数字图像处理:空间滤波基础
空间滤波机理
使用空间域模板进行的图像处理,称为空域滤波。模板本身被称为空域滤波器。输出图像中的每一点为输入图像中某个相关区域像素集的映射。
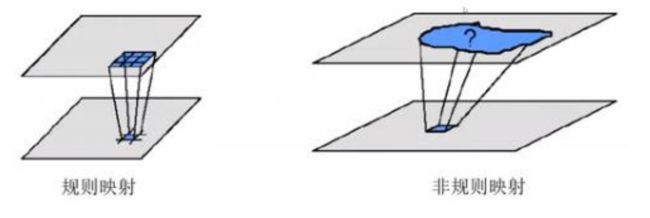
空间滤波相关概念及理解
- 空间滤波是图像处理领域广泛应用的主要工具之一;
- “滤波”一次借用于频域处理,其本意是指接受或拒绝一定的频率分量;
- 空间滤波器作用于图像,可以完成平滑、锐化等类似操作;
- 空间滤波器又称作掩模、掩膜、核、模板或窗口;
- 通过掩模操作实现一种邻域运算,待处理像素点的结果由邻域的图像像素以及相应的与邻域有相同维数的子图像得到;
- 模板的形式并没有必要限制为矩形,矩形只是在数学上易于描述而已;
- 掩模子图像中的值是系数值/权重值,不是灰度值。
步骤
建立模板,在待处理的图像中逐点移动模板,对每个像素点按照滤波器算法进行计算。
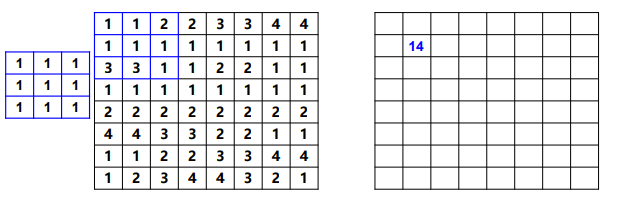
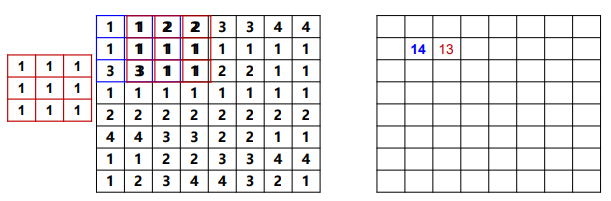
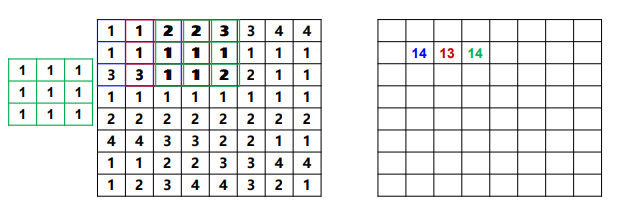
示例
比如,在 M ∗ N M*N M∗N的图像 f f f上,使用 m ∗ n m*n m∗n的滤波器:
g ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x + s , y + t ) g(x,y)=\sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x+s,y+t) g(x,y)=s=−a∑at=−b∑bw(s,t)f(x+s,y+t)
其中, m = 2 a + 1 , n = 2 b + 1 m=2a+1,n=2b+1 m=2a+1,n=2b+1, w ( s , t ) w(s,t) w(s,t)是滤波器系数, f ( x , y ) f(x,y) f(x,y)是图像像素值。
图示:

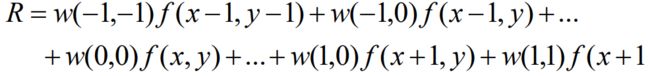
空间相关与卷积
已知:图像 f ( x , y ) f(x,y) f(x,y), m ∗ n m*n m∗n滤波器 w ( x , y ) w(x,y) w(x,y),其中, m = 2 a + 1 , n = 2 b + 1 m=2a+1,n=2b+1 m=2a+1,n=2b+1.
相关操作:
书中的运算符号是一个空心星星,这里我用一个空心菱形。
w ( x , y ) ⋄ f ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x + s , y + t ) w(x,y)\diamond f(x,y)=\sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x+s,y+t) w(x,y)⋄f(x,y)=s=−a∑at=−b∑bw(s,t)f(x+s,y+t)
卷积操作:
w ( x , y ) ⋆ f ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x − s , y − t ) w(x,y)\star f(x,y)=\sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x-s,y-t) w(x,y)⋆f(x,y)=s=−a∑at=−b∑bw(s,t)f(x−s,y−t)
实际上,卷积操作实际上是滤波器旋转180°的相关操作。(如果理解有误,请大佬指正)
卷积的具体示例可以参考书中例子。