数字图像处理课程作业0-骨架图像增强
写在最前
这是我大学课程的数字图像处理的实验报告,可以直接运行。内容比较详细,但是希望大家能够先理解一下思路再使用,学习图像处理的思路最重要。
1.实验目的
掌握各种灰度变换技术,加深对灰度变换的理解;掌握在空域中进行图像噪声消除、图像平滑和图像锐化等各种改善图像质量的方法;通过联合应用实验,提高同学门灵活运用知识的能力。
2.实验要求
将下列图,运用综合的图像的空间域增强进行增强,以方便医生观察骨骼情况。
3.实验分析
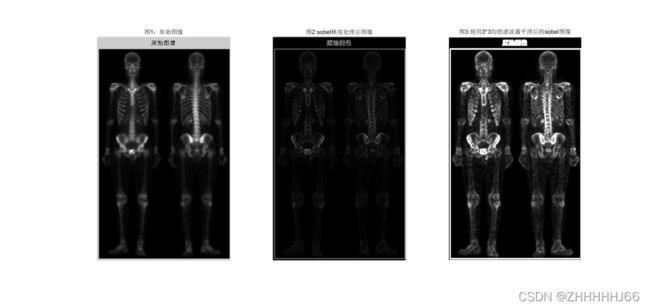
①原图骨架轮廓边缘不够清洗,需要使用边缘算子进行处理,可以使用Sobel梯度算子去除慢变化背景
②对Sobel梯度算子处理后的图片进行3*3的均值滤波
③原图的低灰度区对比度差,窄带高灰度区(亮)需展宽,因此选γ<1的幂次变换
4.实验图像处理技术
4.1 Sobel梯度操作
Sobel算子根据像素点上下、左右邻点灰度加权差,在边缘处达到极值这一现象检测边缘。对噪声具有平滑作用,提供较为精确的边缘方向信息,边缘定位精度不够高。当对精度要求不是很高时,是一种较为常用的边缘检测方法
4.2 均值滤波器
均值滤波是典型的线性滤波算法,它是指在图像上对目标像素给一个模板,该模板包括了其周围的临近像素(以目标像素为中心的周围8个像素,构成一个滤波模板,即包括目标像素本身),再用模板中的全体像素的平均值来代替原来像素值
4.3 幂律变换
伽马变换可以很好地拉伸图像的对比度,扩展灰度级。由图可知,当图像的整体灰度偏暗时,选择y<1,可以使图像
增亮;当图像整体灰度偏亮时,选择y>1,可以使图像变暗,提高图像的对比度,凸显细节。
5.实验代码实现
5.1 读取原图并对原图进行双精度和二维灰度化处理
- 实现代码:
% 读取图片
im=imread('C:\Users\zh006\Desktop\数字图像处理\img\guge.py.png');
% 将图像转换为双精度值
im=im2double(im);
%---原始图像
subplot(1,3,1);
imshow(im);
title('图1:原始图像');
5.2 对原图像试用Sobel梯度操作
- 实现代码:
%---图2,对原图像试用Sobel梯度操作,分量gx为[-1,-2,-1;0,0,0;1,2,1],而分量gy为[-1,0,1;-2,0,2;-1,0,1]的模板。
subplot(1,3,2);
hx=[-1,-2,-1;0,0,0;1,2,1];%生产sobel垂直梯度模板
hy=[-1,0,1;-2,0,2;-1,0,1];%生产sobel水平梯度模板
gradx=filter2(hx,im,'same');
gradx=abs(gradx);%计算图像的sobel垂直梯度
grady=filter2(hy,im,'same');
grady=abs(grady);%计算图像的sobel水平梯度
im3=gradx+grady;%得到图像的sobel梯度
imshow(im3,[]);
title('图2:sobel梯度处理后图像');
- 处理效果:
- 处理分析:
对原图Sobel梯度处理后可以看到骨骼的边缘被锐化了,但是由于暗区的灰度值较小,因此骨骼轮廓不怎么明显
5.3 使用大小为3*3的一个均值滤波器得到平滑后的Sobel梯度图像。
- 实现代码:
%---图3,使用大小为3*3的一个均值滤波器得到平滑后的Sobel梯度图像。
subplot(1,3,3);
h1=fspecial('average',3);
im4=imfilter(im3,h1);
imshow(im4);
title('图3:使用3*3均值滤波器平滑后的sobel图像');
- 处理效果:
- 处理分析:
对Sobel梯度图像进行3*3的均值滤波平滑后我们可以看到骨骼的轮廓明显了,不过骨骼与周围图像的对比还是不够明显
5.4 我们希望扩展灰度范围,对图5进行幂率变换处理,r=0.5,c=1.1,然后即可对图像进行幂率变换
- 实现代码
subplot(1,4,4);
gamma=0.5;
c=1.2;
im7=c.*im4.^gamma;
imshow(im7);
title('图4:图3进行幂率变换后的图像');
- 处理效果:
- 处理分析:
对3*3平滑后的图像进行幂律变换暗区灰度延伸后,我们可以看到处理后的图像和原图比起来,骨骼轮廓清晰了许多,里面的细节也较为明显
-
完整代码
%%%%骨骼图像处理
% 读取图片
im=imread('C:\Users\zh006\Desktop\数字图像处理\img\guge.py.png');
% 将图像转换为双精度值
im=im2double(im);
%---原始图像
subplot(1,4,1);
imshow(im);
title('图1:原始图像');
% conv2函数和filter2函数是用于二维卷积的
%读取图像后,紧接着需要用rgb2gray函数将图像转换为二维的灰度值,否则会报错
im = rgb2gray(im);
%---图4,对原图像试用Sobel梯度操作,分量gx为[-1,-2,-1;0,0,0;1,2,1],而分量gy为[-1,0,1;-2,0,2;-1,0,1]的模板。
subplot(1,4,2);
hx=[-1,-2,-1;0,0,0;1,2,1];%生产sobel垂直梯度模板
hy=[-1,0,1;-2,0,2;-1,0,1];%生产sobel水平梯度模板
gradx=filter2(hx,im,'same');
gradx=abs(gradx);%计算图像的sobel垂直梯度
grady=filter2(hy,im,'same');
grady=abs(grady);%计算图像的sobel水平梯度
im3=gradx+grady;%得到图像的sobel梯度
imshow(im3,[]);
title('图2:sobel梯度处理后图像');
%---图5,使用大小为3*3的一个均值滤波器得到平滑后的Sobel梯度图像。
subplot(1,4,3);
h1=fspecial('average',3);
im4=imfilter(im3,h1);
imshow(im4);
title('图3:使用3*3均值滤波器平滑后的sobel图像');
%--我们希望扩展灰度范围,对图5进行幂率变换处理,r=0.5,c=1,然后即可对图像进行幂率变换
subplot(1,4,4);
gamma=0.5;
c=1.2;
im7=c.*im4.^gamma;
imshow(im7);
title('图4:图3进行幂率变换后的图像');
6.实验收获和结语
完成这次实验后我发现在面对一个有缺陷的图像时我们应该先学会分析,根据它的不完美特点来对症下药,运用各种基础的图像变换组合就可以得到很好的效果。在实验过程中我也遇到了许多问题,例如conv2函数和filter2函数是用于二维卷积的读取图像后,直接运用原图会报错,因此rgb2gray函数将图像转换为二维的灰度值才将问题解决,均值滤波器选择也是尝试许多次才选择了3*3均值滤波器效果才更好。
写在最后
如果觉得写的不错的小伙伴记得给个赞哦!欢迎评论与我交流!