注意力机制 Attention
注意力机制
-
- 前沿
- 注意力
-
- 认知神经学中的注意力
- 人工神经网络中的注意力机制
- HAN(Hierarchical Attention Networks)
- Bi-LSTM + Attention + tensorflow
- 参考文献
前沿
智慧的艺术是知道该忽视什么。 — 威廉·詹姆斯
根据通用近似定理,前馈网络和循环网络都有很强的能力。但由于优化算法和计算能力的限制,在实践中很难达到通用近似的能力。特别是在处理复杂任务时,比如需要处理大量的输入信息或者复杂的计算流程时,目前计算机的计算能力依然是限制神经网络发展的瓶颈。
为了减少计算复杂度,通过部分借鉴生物神经网络的一些机制,我们引入了局部连接、权重共享以及汇聚操作来简化神经网络结构。虽然这些机制可以有效缓解模型的复杂度和表达能力之间的矛盾,但是我们依然希望在不“过度”增加模型复杂度(主要是模型参数)的情况下来提高模型的表达能力。以阅读理解任务为例,给定的背景文章(Background Document)一般比较长,如果用循环神经网络来将其转换为向量表示,那么这个编码向量很难反映出背景文章的所有语义。在比较简单的任务(比如文本分类)中,只需要编码一些对分类有用的信息,因此用一个向量来表示文本语义是可行的。但是在阅读理解任务中,编码时还不知道可能会接收到什么样的问句。这些问句可能会涉及到背景文章的所有信息点,因此丢失任何信息都可能导致无法正确回答问题。
神经网络中可以存储的信息量称为网络容量(Network Capacity)。一般来讲,利用一组神经元来存储信息时,其存储容量和神经元的数量以及网络的复杂度成正比。如果要存储越多的信息,神经元数量就要越多或者网络要越复杂,进而导致神经网络的参数成倍地增加。
我们人脑的生物神经网络同样存在网络容量问题,人脑中的工作记忆大概只有几秒钟的时间,类似于循环神经网络中的隐状态。而人脑每个时刻接收的外界输入信息非常多,包括来自于视觉、听觉、触觉的各种各样的信息。但就视觉来说,眼睛每秒钟都会发送千万比特的信息给视觉神经系统。人脑在有限的资源下,并不能同时处理这些过载的输入信息。大脑神经系统有两个重要机制可以解决信息过载问题:注意力和记忆机制。
我们可以借鉴人脑解决信息过载的机制,从两方面来提高神经网络处理信息的能力。一方面是注意力,通过自上而下的信息选择机制来过滤掉大量的无关信息;另一方面是引入额外的外部记忆,优化神经网络的记忆结构来提高神经网络存储信息的容量。
注意力
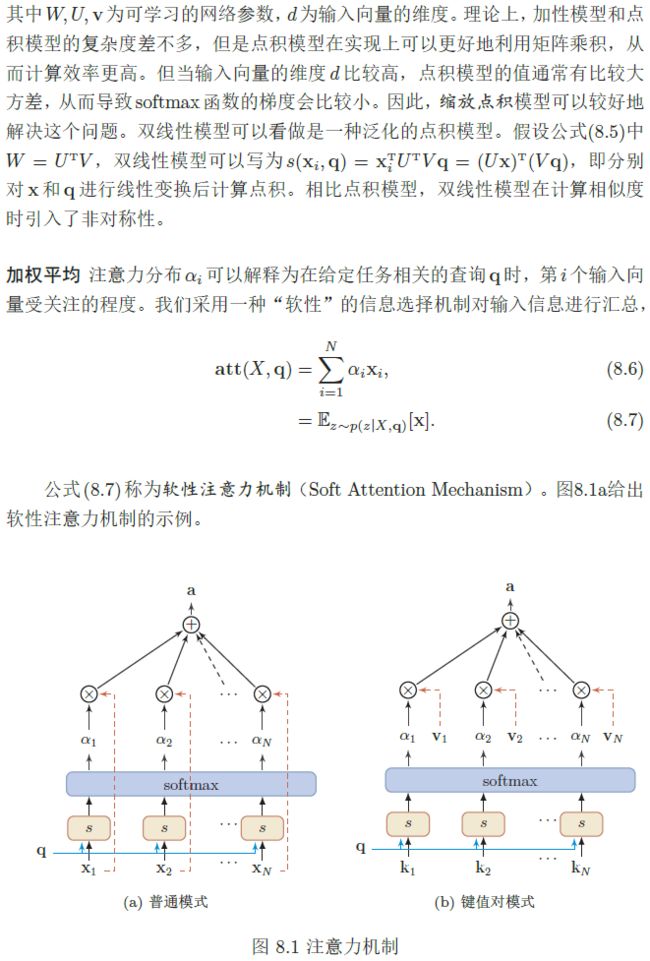
在计算能力有限情况下,注意力机制(Attention Mechanism)作为一种资源分配方案,将计算资源分配给更重要的任务,是解决信息超载问题的主要手段。
认知神经学中的注意力
人工神经网络中的注意力机制
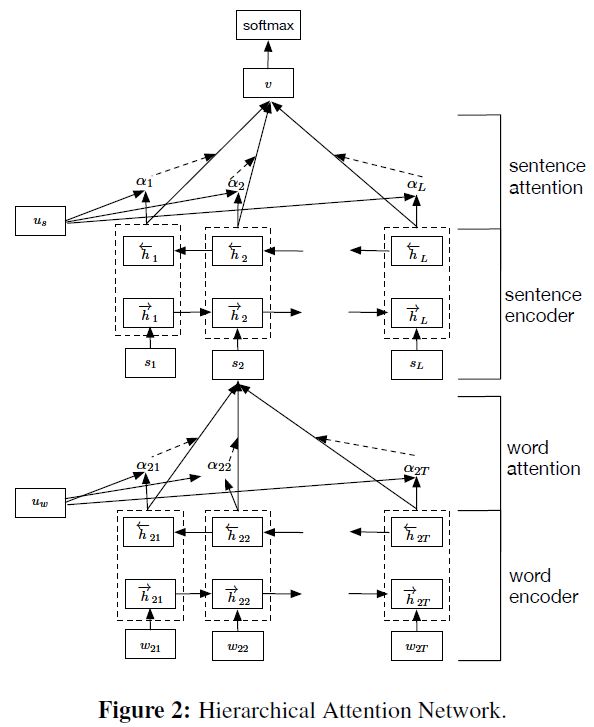
HAN(Hierarchical Attention Networks)
Bi-LSTM + Attention + tensorflow
class BiLSTMAttention(object):
"""
Bi-LSTM + Attention 用于文本分类
"""
def __init__(self, config, wordEmbedding):
# 定义模型的输入
self.inputX = tf.placeholder(tf.int32, [None, config.sequenceLength], name="inputX")
self.inputY = tf.placeholder(tf.float32, [None, 1], name="inputY")
self.dropoutKeepProb = tf.placeholder(tf.float32, name="dropoutKeepProb")
# 定义l2损失
l2Loss = tf.constant(0.0)
# 词嵌入层
with tf.name_scope("embedding"):
# 利用预训练的词向量初始化词嵌入矩阵
self.W = tf.Variable(tf.cast(wordEmbedding, dtype=tf.float32, name="word2vec") ,name="W")
# 利用词嵌入矩阵将输入的数据中的词转换成词向量,维度[batch_size, sequence_length, embedding_size]
self.embeddedWords = tf.nn.embedding_lookup(self.W, self.inputX)
# 定义两层双向LSTM的模型结构
with tf.name_scope("Bi-LSTM"):
for idx, hiddenSize in enumerate(config.model.hiddenSizes):
with tf.name_scope("Bi-LSTM" + str(idx)):
# 定义前向LSTM结构
lstmFwCell = tf.nn.rnn_cell.DropoutWrapper(tf.nn.rnn_cell.LSTMCell(num_units=hiddenSize, state_is_tuple=True),
output_keep_prob=self.dropoutKeepProb)
# 定义反向LSTM结构
lstmBwCell = tf.nn.rnn_cell.DropoutWrapper(tf.nn.rnn_cell.LSTMCell(num_units=hiddenSize, state_is_tuple=True),
output_keep_prob=self.dropoutKeepProb)
# 采用动态rnn,可以动态的输入序列的长度,若没有输入,则取序列的全长
# outputs是一个元组(output_fw, output_bw),其中两个元素的维度都是[batch_size, max_time, hidden_size],fw和bw的hidden_size一样
# self.current_state 是最终的状态,二元组(state_fw, state_bw),state_fw=[batch_size, s],s是一个元祖(h, c)
outputs_, self.current_state = tf.nn.bidirectional_dynamic_rnn(lstmFwCell, lstmBwCell,
self.embeddedWords, dtype=tf.float32,
scope="bi-lstm" + str(idx))
# 对outputs中的fw和bw的结果拼接 [batch_size, time_step, hidden_size * 2], 传入到下一层Bi-LSTM中
self.embeddedWords = tf.concat(outputs_, 2)
# 将最后一层Bi-LSTM输出的结果分割成前向和后向的输出
outputs = tf.split(self.embeddedWords, 2, -1)
# 在Bi-LSTM+Attention的论文中,将前向和后向的输出相加
with tf.name_scope("Attention"):
H = outputs[0] + outputs[1]
# 得到Attention的输出
output = self.attention(H)
outputSize = config.model.hiddenSizes[-1]
# 全连接层的输出
with tf.name_scope("output"):
outputW = tf.get_variable(
"outputW",
shape=[outputSize, 1],
initializer=tf.contrib.layers.xavier_initializer())
outputB= tf.Variable(tf.constant(0.1, shape=[1]), name="outputB")
l2Loss += tf.nn.l2_loss(outputW)
l2Loss += tf.nn.l2_loss(outputB)
self.predictions = tf.nn.xw_plus_b(output, outputW, outputB, name="predictions")
self.binaryPreds = tf.cast(tf.greater_equal(self.predictions, 0.5), tf.float32, name="binaryPreds")
# 计算二元交叉熵损失
with tf.name_scope("loss"):
losses = tf.nn.sigmoid_cross_entropy_with_logits(logits=self.predictions, labels=self.inputY)
self.loss = tf.reduce_mean(losses) + config.model.l2RegLambda * l2Loss
def attention(self, H):
"""
利用Attention机制得到句子的向量表示
"""
# 获得最后一层LSTM的神经元数量
hiddenSize = config.model.hiddenSizes[-1]
# 初始化一个权重向量,是可训练的参数
W = tf.Variable(tf.random_normal([hiddenSize], stddev=0.1))
# 对Bi-LSTM的输出用激活函数做非线性转换
M = tf.tanh(H)
# 对W和M做矩阵运算,W=[batch_size, time_step, hidden_size],计算前做维度转换成[batch_size * time_step, hidden_size]
# newM = [batch_size, time_step, 1],每一个时间步的输出由向量转换成一个数字
newM = tf.matmul(tf.reshape(M, [-1, hiddenSize]), tf.reshape(W, [-1, 1]))
# 对newM做维度转换成[batch_size, time_step]
restoreM = tf.reshape(newM, [-1, config.sequenceLength])
# 用softmax做归一化处理[batch_size, time_step]
self.alpha = tf.nn.softmax(restoreM)
# 利用求得的alpha的值对H进行加权求和,用矩阵运算直接操作
r = tf.matmul(tf.transpose(H, [0, 2, 1]), tf.reshape(self.alpha, [-1, config.sequenceLength, 1]))
# 将三维压缩成二维sequeezeR=[batch_size, hidden_size]
sequeezeR = tf.squeeze(r)
sentenceRepren = tf.tanh(sequeezeR)
# 对Attention的输出可以做dropout处理
output = tf.nn.dropout(sentenceRepren, self.dropoutKeepProb)
return output
参考文献
《神经网络与深度学习》
《Hierarchical Attention Networks for Document Classification》
《Attention-Based Bidirectional Long Short-Term Memory Networks for Relation Classification》