MATLAB实现蚁群算法
直接上代码演示了,运行时记得传参
贪心算法实现,有兴趣可以对比一下:MATLAB实现贪心算法
代码:
%matlab实现ACO
%clc
%clear
%alpha = 1 ; %信息素指数
%beta = 5; %启发指数 表示蚂蚁对其他蚂蚁路径的依赖性
%rho = 0.1 ; %挥发系数 表示蚂蚁对其他蚂蚁路径的依赖性
%n = 20 ; %经过点数
%k = 20 ; %迭代次数
%m = n - 1 ; %蚂蚁只数,这里取比城市数目少一的蚂蚁只数
%Q = 100 ; %默认起始信息素强度为100,收敛速度
function [] = executeACO(alpha,beta,rho,n,k,Q)
%ACO 输入信息素指数,启发指数,挥发指数,经过点数,信息强度
%得到经过算法处理的最优路径图
clc
m = n - 1 ; %蚂蚁只数,这里取比城市数目少一的蚂蚁只数
bestr = inf ; %默认最优路径为无穷大
x = zeros(1,n) ; %产生一个与经过点数相同的行向量
y = zeros(1,n) ;
for i = 1 : (n) %生成20个随机数
x(i) = rand * 20 ;
y(i) = rand * 20 ;
end
d = zeros(n) ;
for i = 1 : n
for j = 1 : n
d(i,j) = sqrt( ( x(i) - x(j) ) ^ 2 + ( y(i) - y(j) ) ^ 2) ; %距离矩阵
end
end
tau = ones(n) ; %信息素矩阵
for i = 1 : k
visited = zeros(m,n) ; %用visited矩阵来储存所有蚂蚁经过的城市
visited(:,1) = (randperm(n,m))'; %将m只蚂蚁随机放在n座城市 即产生一列1到n的随机数进行第一列数据的更新,将visited第一列替换为该列向量
for b = 2 : n %所有蚂蚁都走到第b个城市
current = visited(:,(b-1)) ; %所有蚂蚁现在所在城市
allow = zeros(m,(n - b + 1)) ; %生成一个记录剩下点数的矩阵
for a = 1 : m %依次得到每只蚂蚁剩下的城市,并记录在allow矩阵中
j = 1 ;
for s = 1 : n
if length(find(visited(a,:) == s)) == 0
allow(a,j) = s ;
j = j + 1 ;
end
end
end
l = n-b+1 ; %剩下的城市数量
for a = 1 : m %分析第a只蚂蚁将要前往的下一个点
p = zeros(1,l) ; %产生一个1*l行向量记录要前往的点概率
for j = 1 : l %根据下式来选择下一个城市,用于计算要经过的点的概率
p(j) = ( ( tau( current(a,1) , allow(a,j) ) ) ^ alpha ) * ( ( 1 / d( current(a,1) , allow(a,j) ) ) ^ beta ) ;
end
p = cumsum(p ./ sum(p)) ; %得到经过各个点的概率并进行了累加
pick = rand ; %产生一个用于判断的随机数
for c = 1 : l
if pick < p(c)
visited(a,b) = allow(a,c) ; %将符合的点记录在visited矩阵中
break ;
end
end
end
end
L = zeros(1,m) ;
for a = 1 : m
t = d(visited(a,n),visited(a,1)) ;
for b = 1 : (n - 1)
t = t + d(visited(a,b),visited(a,(b + 1)));
end
L(a) = t ; %记录每只蚂蚁经过所有点的距离
end
[newbestr,newbestant] = min(L) ; %寻本次迭代最短路径及其相应蚂蚁
if newbestr < bestr %如果得到的最优路径比之前的最优路径短则保存位当前最优路径
bestr = newbestr ;
bestroad = visited(newbestant,:) ; %按顺序储存最优路径的坐标值
end
%更新信息素矩阵
for a = 1 : m
tau(visited(a,n),visited(a,1)) = tau(visited(a,n),visited(a,1)) * (1 - rho) ; %信息素挥发
tau(visited(newbestant,n),visited(newbestant,1)) = tau(visited(newbestant,n),visited(newbestant,1)) + Q / L(newbestant) ; %信息素加强
for b = 1 : (n - 1)
tau(visited(a,b),visited(a,(b + 1))) = tau(visited(a,b),visited(a,(b + 1))) * (1 - rho) ;
tau(visited(newbestant,b),visited(newbestant,(b + 1))) = tau(visited(newbestant,b),visited(newbestant,(b + 1))) + Q / L(newbestant) ;
end
end
end
bestx = zeros(1,n) ; %两个1*n阶矩阵按顺序储存坐标点
besty = zeros(1,n) ;
for i = 1 : n
bestx(i) = x(bestroad(i)) ; %将点集坐标保存在两个矩阵中
besty(i) = y(bestroad(i)) ;
end
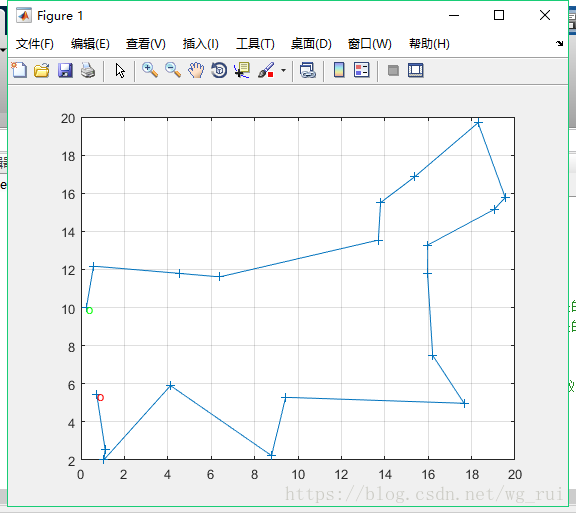
plot(bestx,besty,'-+') ; %用'+'标记出随机点并用实线连接得到最优路径
grid on
text(bestx(n),besty(n),'o','color','r'); %终点为红色圆圈
text(bestx(1),besty(1),'o','color','g'); %起点为绿色圆圈
end
运行结果: