games101——作业8

安装依赖

本次作业需要预先安装 OpenGL, Freetype 还有 RandR 这三个库。可以通过以下命令进行安装：

$ sudo apt install libglu1-mesa-dev freeglut3-dev mesa-common-dev

$ sudo apt install xorg-dev #会自动安装 libfreetype6-det

连接绳子的约束

在 rope.cpp 中, 实现 Rope 类的构造函数。这个构造函数应该可以创建一个新的绳子(Rope) 对象，该对象从 start 开始，end 结束，包含 num_nodes 个节点。也就是如下图所示：
每个结点都有质量，称为质点；质点之间的线段是一个弹簧。通过创建一系列的
质点和弹簧，你就可以创建一个像弹簧一样运动的物体。
pinned_nodes 设置结点的索引。这些索引对应结点的固定属性 (pinned attribute) 应该设置为真（他们是静止的）。对于每一个结点，你应该构造一个 Mass 对象，并在 Mass 对象的构造函数里设置质量和固定属性。（请仔细阅读代码，确定传递给构造函数的参数）。你应该在连续的两个结点之间创建一个弹簧，设置弹簧两端的结点索引和弹簧系数 k，请检查构造函数的签名以确定传入的参数。

 Rope::Rope(Vector2D start, Vector2D end, int num_nodes, float node_mass, float k, vector<int> pinned_nodes)
    {
        // TODO (Part 1): Create a rope starting at `start`, ending at `end`, and containing `num_nodes` nodes.
        for(int i=0; i<num_nodes; ++i) {
            Vector2D pos = start + (end - start) * ((double)i / ((double)num_nodes - 1.0));          
            masses.push_back(new Mass(pos, node_mass, false));
            // masses[i]->forces = Vector2D(0, 0);
        }

        for(int i=0; i<num_nodes-1; ++i) {
            springs.push_back(new Spring(masses[i], masses[i+1], k));
        }

//        Comment-in this part when you implement the constructor
       for (auto &i : pinned_nodes) {
           masses[i]->pinned = true;
       }
    }

运行 ./ropesim。你应该可以看到屏幕上画出绳子，但它不发生运动。

---

显式/半隐式欧拉法

胡克定律表示弹簧连接的两个质点之间的力和他们之间的距离成比例。也就是：

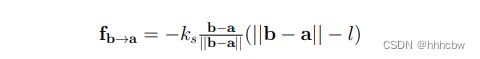
在 Rope::simulateEuler 中, 首先实现胡克定律。遍历所有的弹簧，对弹簧两端的质点施加正确的弹簧力。保证力的方向是正确的！对每个质点，累加所有的弹簧力。

		for (auto &s : springs)
        {
            // TODO (Part 2): Use Hooke's law to calculate the force on a node
            auto len = (s->m1->position - s->m2->position).norm();
            s->m1->forces += -s->k * (s->m1->position - s->m2->position) / len * (len - s->rest_length);
            s->m2->forces += -s->k * (s->m2->position - s->m1->position) / len * (len - s->rest_length); 
        }

一旦计算出所有的弹簧力，对每个质点应用物理定律：

显示欧拉法

下一个位置用当前速度计算得到

            if (!m->pinned)
            {
                // TODO (Part 2): Add the force due to gravity, then compute the new velocity and position
                auto a = m->forces / m->mass + gravity;
                m->position += m->velocity * delta_t; // For explicit method
                m->velocity += a * delta_t; 

                // TODO (Part 2): Add global damping
        	}

显式欧拉运行之后，会发现绳子飞了，因为显式欧拉不收敛或者不稳定

半隐式欧拉

半隐式欧拉使用下一时间的速度计算下一时间的位置

			if (!m->pinned)
            {
                // TODO (Part 2): Add the force due to gravity, then compute the new velocity and position
                auto a = m->forces / m->mass + gravity;                
                m->velocity += a * delta_t; 
                m->position += m->velocity * delta_t; // For semi-implicit method
                // TODO (Part 2): Add global damping
            }

运行 ./ropesim。结果如下

只有 3 个结点，看起来不够多。在 application.cpp 文件的最上方，你应该可以看到欧拉绳子和 Verlet 绳子的定义。改变两个绳子结点个数（默认为 3 个），比如 16 或者更多。这里使用 16 个结点，结果如下：

我们也可以使用 ./ropesim -s 32 来设置仿真中每帧的仿真步数为 32，默认是 64，我们发现小的步数，会更不容易趋于稳定(在后面加入摩擦力之后可以更容易看出)，使用更大的步数，会更容易趋于稳定。

---

显式 Verlet

Verlet 是另一种精确求解所有约束的方法。这种方法的优点是只处理仿真中顶点的位置并且保证四阶精度。和欧拉法不同，Verlet积分按如下的方式来更新
下一步位置：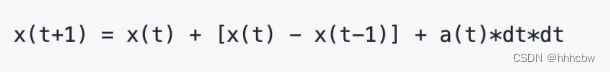

 void Rope::simulateVerlet(float delta_t, Vector2D gravity)
    {
        for (auto &s : springs)
        {
            // TODO (Part 3): Simulate one timestep of the rope using explicit Verlet （solving constraints)
            auto len = (s->m1->position - s->m2->position).norm();
            s->m1->forces += -s->k * (s->m1->position - s->m2->position) / len * (len - s->rest_length);
            s->m2->forces += -s->k * (s->m2->position - s->m1->position) / len * (len - s->rest_length);
        }

        for (auto &m : masses)
        {
            if (!m->pinned)
            {
                Vector2D temp_position = m->position;
                auto a = m->forces / m->mass + gravity;
                // TODO (Part 3.1): Set the new position of the rope mass
                m->position = temp_position + (temp_position - m->last_position) + a * delta_t * delta_t;
                m->last_position = temp_position;
            }
            m->forces = Vector2D(0, 0);
        }
    }
}

运行结果如下
除此之外，我们可以仿真弹簧系数无限大的弹簧。不用再考虑弹簧力，而是用解
约束的方法来更新质点位置：只要简单的移动每个质点的位置使得弹簧的长度保
持原长。修正向量应该和两个质点之间的位移成比例，方向为一个质点指向另一
质点。每个质点应该移动位移的一半。

只要对每个弹簧执行这样的操作，我们就可以得到稳定的仿真。为了使运动更加
平滑，每一帧可能需要更多的仿真次数。

---

阻尼

向显示 Verlet 方法积分的胡克定律中加入阻尼。现实中的弹簧不会永远跳动-因为动能会因摩擦而减小。阻尼系数设置为 0.00005, 加入阻尼之后质点位置更新如下：

for (auto &m : masses)
        {
            if (!m->pinned)
            {
                Vector2D temp_position = m->position;
                auto a = m->forces / m->mass + gravity;
                double damping_factor = 0.00005;
                // TODO (Part 4): Add global Verlet damping
                m->position = temp_position + (1 - damping_factor) * (temp_position - m->last_position) + a * delta_t * delta_t; 

                m->last_position = temp_position;
            }
            m->forces = Vector2D(0, 0);
        }
    }

./ropesim 会发现绳子最后趋于静止，由于能量损失
运行 ./ropesim -s 256 会发现静止的更快了
而向欧拉方法中加入阻尼，参考助教关于作业8的一些解答，直接使用 $-k_{d}v$ 作为阻尼，而不是相对速度

float kd = 0.005; // damping coefficient
if (!m->pinned)
            {
                // TODO (Part 2): Add the force due to gravity, then compute the new velocity and position

                // TODO (Part 2): Add global damping
                auto a = m->forces / m->mass + gravity - kd * m->velocity / m->mass;
                m->velocity += a * delta_t;
                m->position += m->velocity * delta_t;
            }

运行 ./ropesim 结果如下