初识神经网络和反向传播算法

今天来看一下西瓜书第五章——神经网络。

以下介绍的是人工神经网络，是模拟生物神经网络进行信息处理的一种数学模型。

定义

神经网络最基本的成分是神经元模型，生物中如果某神经元的电位超过某个阈值，那么它就会被激活，向其他神经元发送化学物质。

以下是 M-P 神经元模型，由输入的信号 $x_i$ 赋予权重 $w_i$ 之后，对应相乘求和，通过阈值 $\theta$ 比较，最后通过激活函数输出 0/1 一个新的神经元。

常用的激活函数有以下 4 种：

感知机与多层网络

感知机接收多个信号，输出一个信号。

$$y=\{\begin{array}{l}0,{\sum }_{i=1}^n{w}_i{x}_i\le \theta \\ \\ 1,{\sum }_{i=1}^n{w}_i{x}_i>\theta \end{array}$$

感知机的学习规则：

对训练样例 $(x,y)$，若当前的感知机输出为 $\hat{y}$，则感知机权重调整如下：

• $w_i\leftarrow w_i+\Delta w_i$，$\Delta w_i=\eta (y-\hat{y})x_i$
• 其中 $\eta \in (0,1)$ 称为学习率，学习率越高，梯度下降的越快。

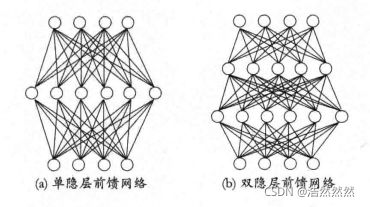
多层网络，即输入层和输出层还有多层神经元，称为隐含层。隐含层和输出层的神经元都需要通过激活函数生成。

更一般的，若每层神经元没有同层连接，也没有跨层连接，我们称该网络为多层前馈神经网络，当然，前馈并不意味着网络信号不能向后传，只是没有环或回路即可。例子如下图：

误差逆传播算法

误差逆传播算法简称 BP 算法，该算法不仅能训练多层前馈神经网络，也能训练递归神经网络。

给定训练集 $D=\left\{(x_1,y_1),\cdots ,(x_m,y_m)\right\}$，其中 $x_i\in R^d$，$y_i\in R^l$，分别为 $d$ 维和 $l$ 维的实数域。

为了方便描述，假定网络只有一个隐含层。

• 不妨设输入层有 $d$ 个神经元，隐含层有 $q$ 个神经元，输出层有 $l$ 个神经元。
• 隐含层第 $h$ 个神经元阈值为 ${\gamma }_h$
• 输出层第 $j$ 个神经元阈值为 ${\theta }_j$
• 输入层第 $i$ 和隐含层第 $h$ 个神经元的权值为 $v_{ih}$
• 隐含层第 $h$ 和输出层第 $j$ 个神经元的权值为 $w_{hj}$。
• 隐含层第 $h$ 个神经元的输入为 ${\alpha }_h={\sum }_{i=1}^d{v}_{ih}{x}_i$
• 输出层第 $j$ 个神经元的输入为 ${\beta }_j={\sum }_{h=1}^q{w}_{hj}{b}_h$

其中 $b_h$ 为隐含层第 $h$ 个神经元的输出值，即 $b_h=Sigmoid({\alpha }_h-{\gamma }_h)$

那么，对样本 $(x_k,y_k)$ 来说，若输出为 ${\hat{y}}_k=({\hat{y}}_1^k,\cdots ,{\hat{y}}_l^k)$，那么就会有

$${\hat{y}}_j^k=Sigmoid({\beta }_j-{\theta }_j)$$

其 $MSE$ 为

$$E_k=\frac{1}{l}\sum _{j=1}^l({\hat{y}}_j^k-y_j^k{)}^2$$

同样的，在训练的每一轮中，用感知机学习规则对参数进行更新，对任意参数 $\xi$ 的更新如下表达式：

$$\xi \leftarrow \xi +\Delta \xi$$

由于 $BP$ 神经网络是基于梯度下降寻最优参数，我们给定一个学习率 $\eta$，以负梯度方向对参数进行调整。

我们的目的是更新如下参数：

$$\xi \in \left\{w_{hj}、{\theta }_j、v_{ih}、{\gamma }_h\right\}$$

即我们要求得：

$$\Delta \xi =\{\begin{array}{l}\Delta w_{hj}=-\eta \frac{\partial E_k}{\partial w_{hj}}\\ \\ \Delta {\theta }_j=-\eta \frac{\partial E_k}{\partial {\theta }_j}\\ \\ \Delta v_{ih}=-\eta \frac{\partial E_k}{\partial v_{ih}}\\ \\ \Delta {\gamma }_h=-\eta \frac{\partial E_k}{\partial {\gamma }_h}\end{array}$$

现在，我们来推导参数的更新。

我们先将 $E_k$ 的公式改写如下：

$$\begin{array}{rl}{E}_k& =\frac{1}{l}\sum _{j=1}^l({\hat{y}}_j^k-y_j^k{)}^2\\ & \\ & =\frac{1}{l}\sum _{j=1}^l(Sigmoid({\beta }_j-{\theta }_j)-y_j^k{)}^2\\ & \\ & =\frac{1}{l}\sum _{j=1}^l(Sigmoid(\sum _{h=1}^q{w}_{hj}{b}_h-{\theta }_j)-y_j^k{)}^2\\ & \\ & =\frac{1}{l}\sum _{j=1}^l(Sigmoid(\sum _{h=1}^q{w}_{hj}Sigmoid(\sum _{i=1}^d{v}_{ih}{x}_i-{\gamma }_h)-{\theta }_j)-y_j^k{)}^2\end{array}$$

注意到 $Sigmoi{d}^{\prime }(x)=Sigmoid(x)(1-Sigmoid(x))$，可以方便我们求导。

于是，容易求得上述参数，如下：

$$\Delta \xi =\{\begin{array}{l}\Delta w_{hj}=-\eta \frac{\partial E_k}{\partial w_{hj}}=\frac{2}{l}\eta {\hat{y}}_j^k(1-{\hat{y}}_j^k)(y_j^k-{\hat{y}}_j^k)b_h\\ \\ \Delta {\theta }_j=-\eta \frac{\partial E_k}{\partial {\theta }_j}=-\frac{2}{l}\eta {\hat{y}}_j^k(1-{\hat{y}}_j^k)(y_j^k-{\hat{y}}_j^k)\\ \\ \Delta v_{ih}=-\eta \frac{\partial E_k}{\partial v_{ih}}=\frac{2}{l}\eta {\sum }_{j=1}^l{w}_{hj}{b}_h(1-b_h){\hat{y}}_j^k(1-{\hat{y}}_j^k)(y_j^k-{\hat{y}}_j^k)x_i\\ \\ \Delta {\gamma }_h=-\eta \frac{\partial E_k}{\partial {\gamma }_h}=-\frac{2}{l}\eta {\sum }_{j=1}^l{w}_{hj}{b}_h(1-b_h){\hat{y}}_j^k(1-{\hat{y}}_j^k)(y_j^k-{\hat{y}}_j^k)\end{array}$$

需要注意的是，$BP$ 神经网络目标是使得 $MSE$ 最小，即求 $min(E=\frac{1}{m}{\sum }_{k=1}^m{E}_k)$

以上是标准的 $BP$ 算法，每次对一个样本进行更新权值和阈值。若推导基于累计误差最小化的更新规则，就有累积 $BP$ 算法。

全剧最小与局部最小

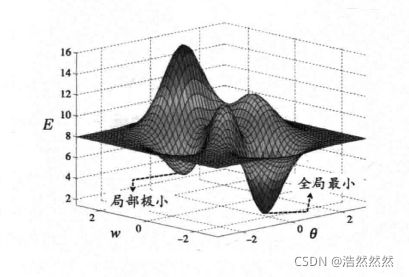
神经网络在迭代求解权值和阈值的过程中，是一个寻优的过程，如果说误差函数有多个极小值，最后找到的结果不一定是最优解，如下图：

因此，我们常采用以下方法进行求解。

• 用多组不同参数值初始化多个神经网络。训练完，取误差最小的解作为参数。
• 用遗传算法寻优。
• 用随机梯度下降寻优。

参考资料

[1] 周志华.机器学习[M].北京:清华大学出版社,2020.