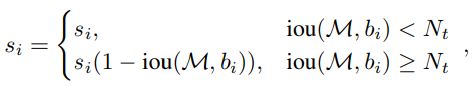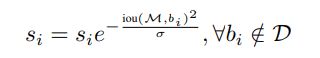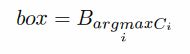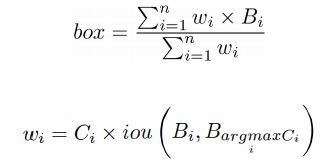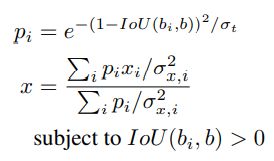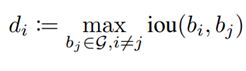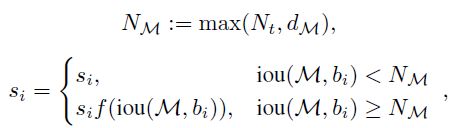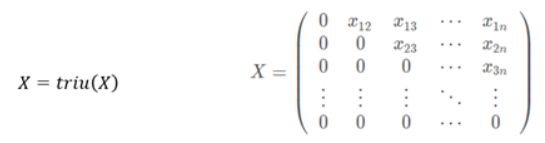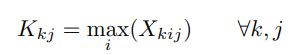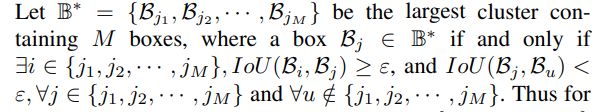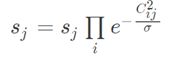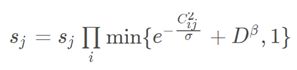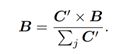目标检测之—非极大抑制(NMS)综述

    非极大值抑制（Non-Maximum Suppression，NMS），顾名思义就是抑制不是极大值的元素。它在目标检测中起着非常关键的作用。

     目标检测一般分为两个过程：训练过程+检测（推理）过程。

     在训练过程中，目标检测算法会根据给定的ground truth调整深度学习网络参数来拟合数据集的目标特征，训练完成后，神经网络的参数固定，因而能够直接对新的图像进行目标预测。      

     然而，在实际的目标预测中，一般的目标检测算法（R-CNN,YOLO等等）都会产生非常多的目标框，其中有很多重复的框定位到同一个目标，NMS作为目标检测的最后一步，用来去除这些重复的框，获得真正的目标框。

     在两阶段目标检测算法中，以Faster-RCNN为例，有两处使用NMS，第一处是在训练的时候，利用ProposalCreator来生成proposal的时候，因为只需要一部分proposal，所以利用NMS进行筛选。第二处使用是在预测的时候，当得到300个分类与坐标偏移结果的时候，需要对每个类别逐一进行非极大值抑制。那为什么对于每个类别不直接取置信度最高的那一个作为最终的预测呢？因为一张图中某个类别可能不止一个，例如一张图中有多个人，直接取最高置信度的只能预测其中的一个人，而通过NMS理想情况下可以使得每个人（每类中的每个个体）都会有且仅有一个bbox框。

     在一阶段目标检测算法中，以YOLOv5为例，输入一张640*640的图像，NMS之前会产生（80*80+40*40+20*20）*3=25200个目标框，这些框都有相应的分类置信度，当置信度满足正样本条件时（比如100个框，这些框密集的分布在目标周围），被送入NMS，NMS后会产生个数位个目标框（比如7个），如下图所示。

      NMS作为计算机视觉中检测的一个组成部分，已经有50年的历史[1]。它首先被应用于边缘检测技术，随后被应用于特征点检测、Face 检测和目标检测中。在边缘检测中，NMS进行边的细化移走伪响应。在特征点检测中，NMS在进行局部阈值以得到独一无二的特征点检测中非常有效。在Face检测中，NMS使用交叠标准划分边界框到不关联的子集。 

     近年来，NMS仍然被应用在现代目标检测器中。也有个别基于学习的方法被提出作为Greedy NMS的替代。在[2]中，首先计算每一对检测框的交叠，然后进行仿射推理聚类，为每个代表最终检测框的类选择一个样例。在[3]中，多类的版本被提出，这里每张图像上所有类的实例被同时评估。  

     本文介绍现代的NMS基本算法及改进算法，具体为：

• 传统的NMS

• 带权的NMS(soft NMS,Weighted NMS,Softer NMS )

• 考虑定位的NMS

• Adaptive NMS

• 并行的NMS(Fast NMS, Cluster NMS)

1  NMS基本算法

     NMS基本算法的具体步骤如下：

          1）依据框的分数（即目标的概率）将所有预测框排序；

          2）选择最大分数的检测框M，将其他与M框重叠度大（IoU超过阈值Nt）的框抑制；

          3）迭代这一过程直到所有框被检测完成。

   

   在NMS中，使用小的阈值Nt（如0.3），将会更多的抑制附近的检测框，从而增加了错失率；而使用大的Nt（如0.7）将会增加假正的情况。当目标个数远远小于RoI个数时，假正的增加将会大于真阳的增加，因此高的NMS不是最优的。

2.  带权的NMS

带权的NMS包含三种算法：Soft—NMS[4], Weighted NMS[5], Softer-NMS[6]

A. Soft-NMS

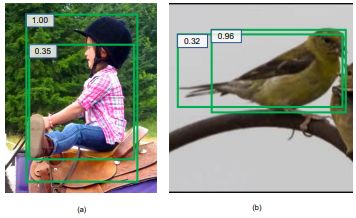
背景：根据传统NMS算法的设计，如果一个真实的目标框的分数满足阈值范围，它就会被抑制掉，如下图所示。

       

解决方案：提出Soft-NMS，降低检测的分数，构成与M重叠度的连续函数，而不是直接删除目标。

Soft-NMS分析：如果检测框M附近的一个检测框b真的包含一个没有被M覆盖的物体，它在低的检测阈值下不会导致错失这个物体；如果检测框b不包含任何物体，那么即使降低了它的分数，它仍然排在真实检测的前面，会产生一个假正的检测。因此NMS考虑了下面的条件。

• 邻域检测的评分应该降低到使假阳性率上升的可能性很小，但高于检测列表中明显的假阳性。

• 用一个低NMS阈值移走相邻的检测框将是次最佳的，它会在用高的重叠率评估时（如[email protected]）增加错失率；

• 当NMS阈值过高时，在重叠范围内测量的平均精度（mAP）将会降低。

Rescoring 函数

       当邻居检测框b与当前框M有大的IoU时，它更应该被抑制，因此分数更低。而远处的框不受影响。

为什么可以这样呢？细想一下，如果gt之间存在overlap的情况，则我们的目的是抑制那些overlap更大的。比如有三个结果ABC,分数分别为0.9,0.8,0.7，其中AC是正确结果，A和B的overlap大于A和C的，这样经过一轮NMS后BC的分数可能就变了0.6，0.5，从而将B抑制了。

然而，上面的公式不是一个连续函数，在Nt处会有一个突然的惩罚。连续的高斯罚函数如下：

      算法伪代码如下：

Soft-NMS是NMS的更通用形式，NMS是Soft-NMS的一种特例。

B. Weighted NMS

  背景：NMS方法在一组候选框中选择分数最大的框作为最终的目标框。然而，非极大的检测结果保存了特征的最大值，因此忽略非极大的检测检测结果是不合适的。

  解决方法：假定所有的Box来自相同的物体，通过考虑非极大结果充分考虑了目标的信息，提出了如下的非极大权重（Non-Maximum Weighting）：

其中n为box的个数，Ci是boxi的置信度。

C. Softer-NMS

     背景：在目标检测数据集中，一些Ground-truth框往往有模糊性（不准确的标注、遮挡、边框模糊）。

       

         (a)两个候选框坐标都不准确 （b）高准确率的框左边界不准确

解决方法：边界框参数化（预测一个分布替代唯一的定位）；训练时边框回归时采取KL损失；一个新的NMS方法提高定位准确性（下图）。

当选择了最大分数的b之后，它的新位置根据它自身和邻居框计算。受Soft-NMS启发，离得越近，不确定性越低，会分配更高的权重。新的坐标计算如下：

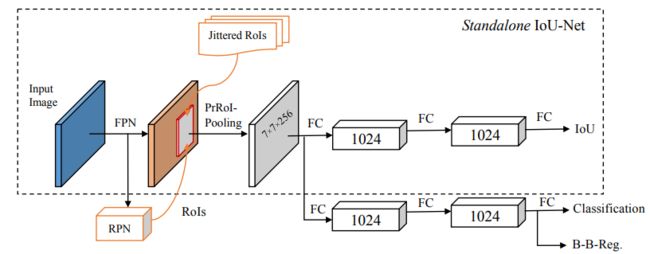
3.  考虑定位的NMS（ IoU-guided NMS）[7]

     背景：当前的目标检测器依赖于边界框的回归和NMS定位目标，分类的概率反映了分类置信度，但定位置信度缺乏，使得定位的准确性降低。以下是目标定位的两个缺点：1.  分类准确率和定位准确率的误匹配；2. 边界框回归的非单调性。

1. 误匹配问题

        黄色：Groud-truth   绿色：位置置信度高  红色：分类置信度高

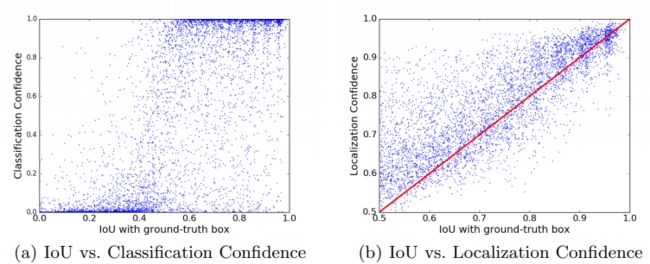
  下图为IoU与分类置信度，定位置信度的相关性示意图。可以看出，IoU与定位置信度高度相关（0.617），而与分类置信度几乎无关（0.217）。

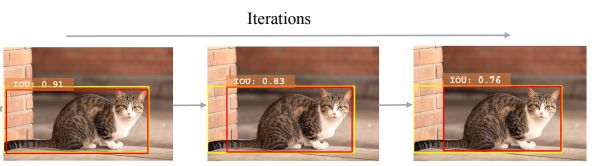
   2. 回归的非单调性

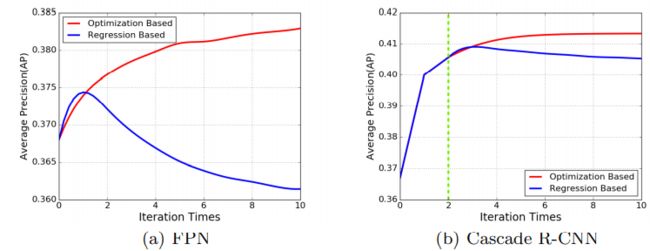
     基于回归的边界框改进，迭代的过程，定位准确率却在降低。

  

      解决方案：提出 IoU-guided NMS，在一般检测的框架中，增加了一个额外的分支用来预测每个框的定位置信度(该框与GT的IoU,下图），然后用预测的IoU代替分类置信度作为NMS排序的关键，消除误导性分类置信度引起的抑制失效。

     

 IoU-guided NMS解耦了定位置信度和分类置信度。利用定位置信度排序检测到的检测框，并基于类似聚类的方法更新分类置信度（当框 i 消除框 j 时，通过 si = max(si , sj ) 更新框 i 的分类置信度 si。这个过程也可以解释为置信聚类：对于一组匹配相同ground-truth的边界框，我们对类别标签进行最有信心的预测）。伪代码如下：

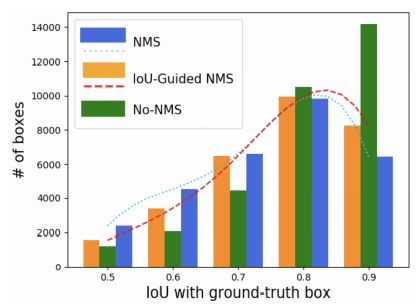
效果：从下图可以看出，传统的NMS（蓝色）中，很多高IoU的被抑制了，而保留了很多低IoU的框， IoU-guided NMS保留了更多准确的定位框。

关于box的迭代回归，下图显示了新方法的单调性。

疑问：既然以前NMS都是采用分类进行排序，说明分类对于NMS是非常有用的，可否将分类和定位准确率统一起来考虑？

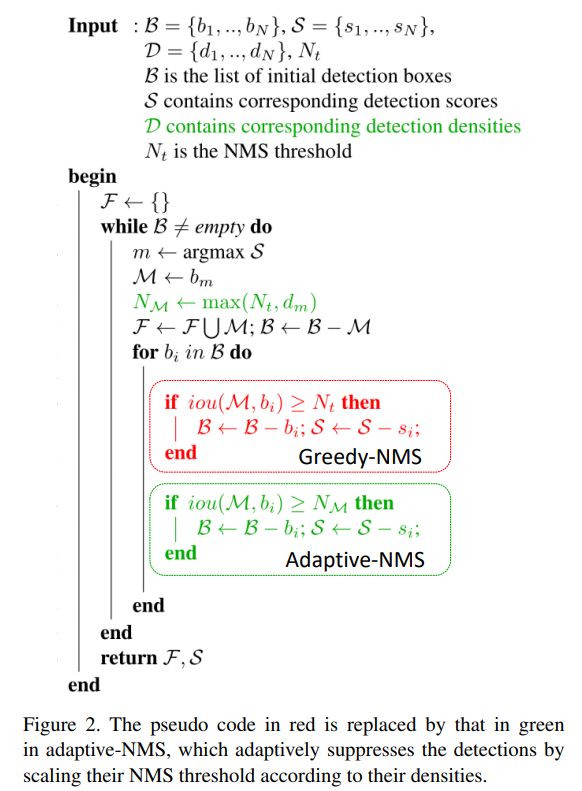
4. Adaptive NMS[8]

背景：使用单一阈值的NMS会面临这种困境：较低的阈值会导致丢失高度重叠的对象（图中蓝框是未检测出来的目标），而较高的阈值会导致更多的误报（红框是检测错误的目标）。这在密集场景下，如行人检测中，会导致较低的准确率。

 

解决方案：Adaptive NMS应用了动态抑制策略，其中阈值随着目标聚集和相互遮挡（密度）而上升，并在目标单独出现时衰减。并设了一个自网络用于学习密度的分数。

具体分析：

• 对于远离M的检测框，它们被误报的可能性较小，因此应该保留它们。

• 对于高度重叠的相邻检测，抑制策略不仅取决于与M的重叠，还取决于M是否位于拥挤区域。如果M位于拥挤的区域，其高度重叠的相邻框很可能是真正的正例，应该分配较轻的惩罚或保留。但是对于稀疏区域中的实例，惩罚应该更高以修剪误报。

首先定义目标密度：对于每个目标的密度，定义如下：

where the density of the object i is defined as the max bounding box IoU with other objects in the ground truth set G. The density of objects indicates the level of crowd occlusion. 

       疑问：这个定义文中给的特别模糊，other objects指的是什么？是完全按照ground truth的密度进行的？还是同属于一个ground truth 的框的集合中，与这个框最大的iou？

依据这个定义，则更新策略为：

其中 NM 表示 M 的Adaptive NMS 阈值，dM 是目标 M 覆盖的密度。

可以看出，这个抑制措施具有三个属性： 

• 当相邻box远离M时，即 IoU(M,bi)

• 如果M位于拥挤区域, 即dM > Nt,则NMS的阈值为M的密度dM。因此，相邻的边框被保留，既然它们非常可能定位到M周围的其他目标。 

• 如果目标在稀疏区域，即 dM<= Nt,  则 NMS的阈值为Nt。 

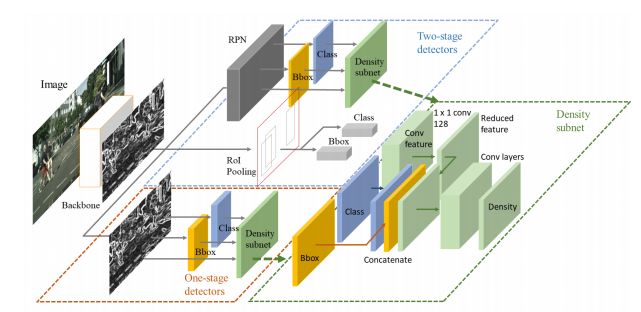
    文中将密度估计看作一个回归问题，使用如下的三层的卷积子网络进行预测,采用Smooth L1 损失。

     因为检测器的输出特征只包含目标本身的信息，也就是语义特征和位置，难以直接进行目标密度的预测，因为密度信息除了需要目标本身的特征图外，还需要周围目标的信息。论文首先使用1*1卷积层降维，然后concatenate降维后的特征与objectness和bounding boxes，作为Density-subnet的输入。而且，在最后一层应用5*5的大卷积核将周围的信息考虑进去。

        疑问：这里，密度网络中将Bbox和class及特征图concate在一起输入给密度网络的物理含义不是很明确。

      Adaptive NMS的伪代码如下，与基本NMS算法相比仅替换了阈值。

 

  5. 并行的NMS 

NMS是检测精度和推理速率的关键瓶颈。基本的NMS由于其顺序迭代的抑制方式以及IoU的逐个计算方式，速度难以提升。因此，将两者并行化是关键。

      得益于GPU的并行计算能力，所有IoU计算可以一次性并行完成。定义IoU矩阵为：

其中B1,…,Bn已按照得分降序排列。

      基于IoU矩阵，有两种对框进行抑制的操作方法：Fast NMS[9]和Cluster NMS[10]。

A. Fast NMS

背景：IoU计算实现了并行化后，NMS的实施也可以通过并行化来大幅提升速度。

解决方法：如果某个框与更高分框的IoU大于阈值，就将其删除。Fast NMS可以并行的决定每个框的去留。为做到这一点，该方法允许已经被删除的框去抑制别的框。具体步骤如下：

• 首先，对每个类别的前n个得分计算大小为

  

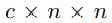
  的 IOU矩阵X（对角矩阵），其中c为类别，并且对每个类别的框进行降序排列。

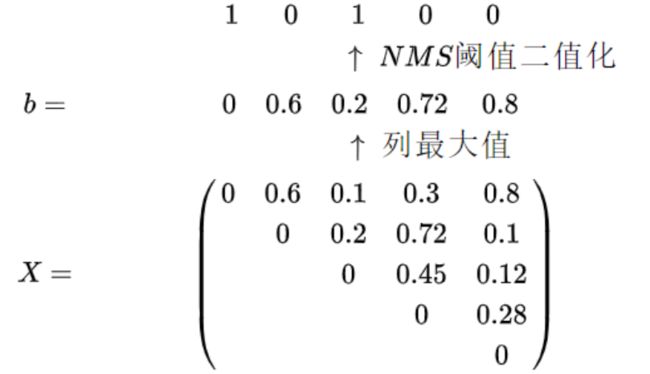
• 然后，将IOU大于阈值的框移走。在实现上，将X的下三角和对角线设置为0（

  

  ）.

  

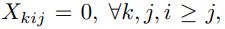
• 然后逐列求最大值得到向量b。

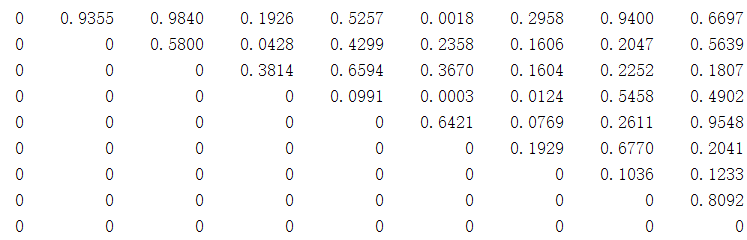
• 最后，利用阈值t（论文取0.5）来处理矩阵，对每个类别保留最优的检测框。这里，NMS的阈值二值化中，1表示保留，0表示抑制。上面图中第一个0保留，只因为它的分值最高（预测框已经按得分降序排列好了），并且每一个元素都是行号小于列号，元素大于阈值就代表着这一列对应的框与比它置信度高的框过于重叠（见下段解释）。

       这个方法非常巧妙，假设有三组不相交的框集合，每组内的框IOU都比较大，组间的IOU非常小。Fast-NMS将会为三组框的每组保留一个框。 这是通过上三角矩阵的设计完成的。假如{{x1 x2 x3}；{x4 x5 x6}；{x7 x8 x9}} 为三组，IOU矩阵按照数字大小排列（这里假如数字越小，得分越高），则因此第四列的IOU只有x4和{x1 x2 x3}三个框的IOU,三个值均很小，因此x4被保留，同样x7也会被保留。

       因此可以说Fast NMS有一定的分组功能，不相交（相交很少）的框集合中的每个集合都会保留一个框。但对于靠近的框集合，Fast NMS则会抑制掉更多的框。

        我们知道NMS的思想是：当一个框是冗余框，被抑制后，将不会对其他框产生任何影响。但在Fast NMS中，如果一个框 Bi的得分比 Bj 高，且Bj 被抑制了，矩阵 X 的第 i 行正是Bi 与得分低于它的所有框的IoU，如果xij 这个元素≥NMS阈值的话，那么在取列最大值这个操作时， b 的第j 个元素必然≥NMS阈值，于是很不幸地 Bj 就被抑制掉了。也就是在前面的例子中，由于第二个框 B2 被抑制（与第一个框相交太多），那么第二行第四列的0.72（box 2和box 4的IoU）就不应该存在，可是Fast NMS允许冗余框去抑制其他框，导致了第四个框 B4 被错误地抑制了。

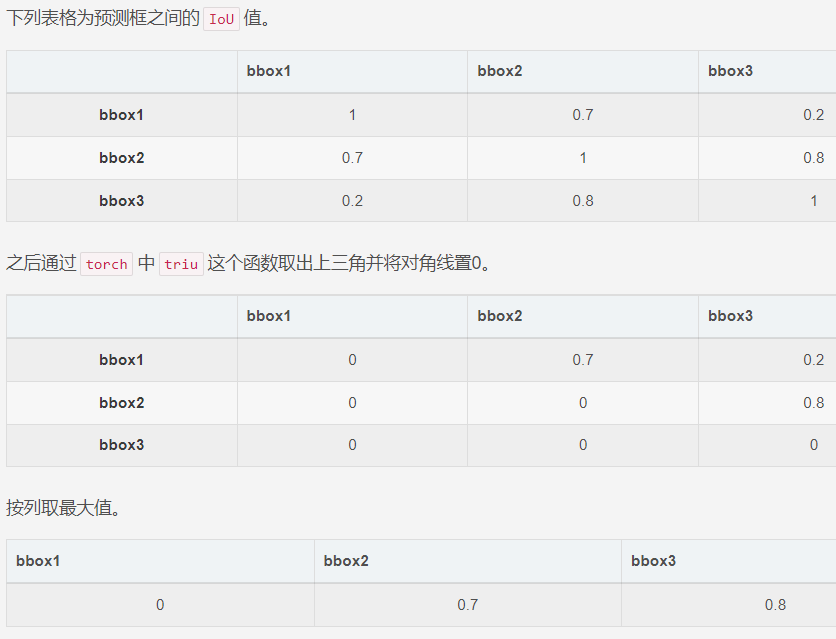
      再看一个简单的实例：

     假设阈值为0.5，那么该类中bbox2和bbox3都要被舍弃，只留下了bbox1。但是如果按照传统的NMS方法，bbox2会被排除，bbox3会被保留。所以Fast NMS会抑制更多的框，故这种做法会造成精度的降低。

B. Cluster-NMS

背景：Fast NMS确实高效，但是抑制了太多框。如果某个框Bi已经被抑制，即使与它的IoU大于阈值（即xij>e），在制定抑制Bj的规则时也应该排除Bi。但是在Fast NMS中，实际上考虑了Bi，这就造成了过度的抑制。

解决方法：引入了一种迭代策略，使得被抑制的框不会再抑制别的框，迭代结束后的结果与传统NMS结果相同。同时由于NMS被并行地执行在隐式的clusters中，Cluster通常只需要更少的迭代次数。

Cluster-NMS中的Cluster是一个框集合，若某一个框A属于这个cluster，则必有cluster中的框与A的IoU≥NMS阈值，且A不会与除这个cluster之外的框有IoU≥NMS阈值。定义如下：

举个简单的例子：

    上图中的黑红蓝橙四个框构成一个cluster，而绿色的两个框构成一个cluster，虽然两个cluster之间有相交，但都没有超过NMS阈值，于是这两个框集合不能合并成一个cluster。

然后我们看一下Cluster NMS是怎么做的？

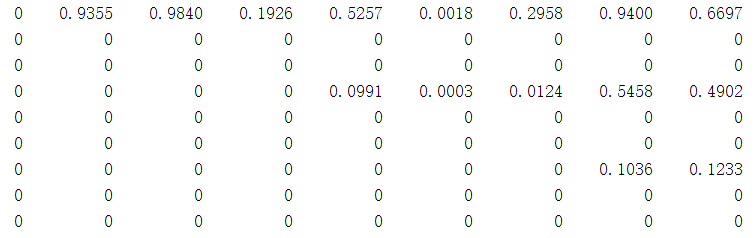
其实就是一个迭代式的Fast NMS。前面的过程与Fast NMS一模一样，都是B 按得分降序排列，计算IoU矩阵，上三角化。然后按列取最大值，经过NMS阈值二值化得到一维张量 b 。但不同于Fast NMS直接输出了 b ，Cluster NMS而是利用b ，将它展开成一个对角矩阵 E 。也就是这个对角矩阵E 的对角线元素与b 相同。然后用 E 去左乘IoU矩阵 X 。然后在再按列取最大值，二值化得到新的b，重复利用b，直到出现某两次迭代后， b 保持不变，那么谁该保留谁该抑制也就确定了。

下面是一个例子：

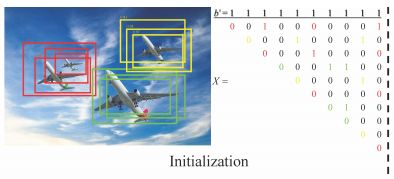
初始化的检测框（其中10个检测到的盒子隐式地分组到3个集群中）

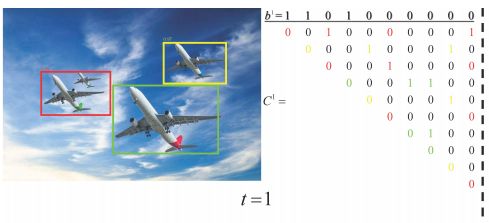
第一次迭代，左边的小飞机目标丢失(Cluster-NMS等价于Fast NMS,其中框被过度抑制)

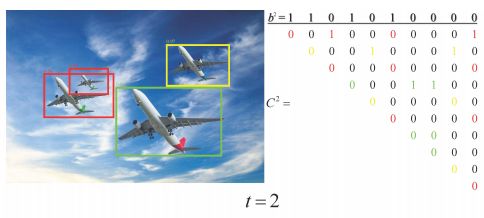
第二次迭代，左边的小飞机目标找回

理论上，Cluster-NMS将最多迭代4次，因为最大的集群(红框)有4个框。而经过2次迭代后的b正是原始NMS的最终结果，说明Cluster-NMS通常需要更少的迭代。

下面再看一个例子。假设的IoU矩阵的下三角矩阵为

    对应的列最大值NMS阈值二值化为   

     可以看出，被抑制的框为{2,3，5,6，8,9}，为了消除被抑制的框再去抑制其他的框，用二值化数列的对角化矩阵左乘X就可以做到。左乘后的下三角矩阵为，被抑制后的框所对应的行全为0.

     该矩阵对应的列最大值NMS阈值二值化为   

 1     0     0     1     1     1     1     0     0

 可以看到被抑制框减少为{2,3，8,9}，其中{5,6}被找回来了。

在继续迭代，发现b不再发生变化，迭代终止。

这种思路特别巧妙，通过较少的迭代次数可将Fast NMS多抑制的框找回。

除此之外，Cluster-NMS能够与多种改进NMS相结合，产生三种变体以提升性能，分别是：1）得分惩罚机制SPM（Score Penalty Mechanism）；2）考虑两框间中心点距离；3）坐标加权。

1）得分惩罚机制SPM

受Soft-NMS的启发，每个框的得分要进行“更新”，使用矩阵C中该列的元素进行惩罚：

2）考虑两框间中心点距离

首先将IoU矩阵X更换为DIoU[11]矩阵；其次，在SPM中的惩罚项中引入归一化中心点距离：

其中D，为归一化中心点距离，b用来控制惩罚程度，同时避免了惩罚因子大于1。

3）坐标加权

受Weighted NMS的启发，所有框按照一定的权重融合在一起，形成新的框。加权方式如下：

其中，我们使用得分向量s = [s1, s2, · · · , sN ]T逐个将C的每一列相乘，得到的C’包含分类分数和IoU。

 

 总结

    NMS在目标检测中的作用非常重要。以上工作考虑了阈值的动态改变（Adaptive NMS），非最大框的辅助作用（带权NMS），以及考虑框的定位信息作为NMS的指导（IoU-guided NMS）。

思考：NMS本身是一个聚类问题。

参考文献

[1]  A. Rosenfeld and M. Thurston. Edge and curve detection for visual scene analysis. IEEE Transactions on computers, 100(5):562–569, 1971. 

[2] R. Rothe, M. Guillaumin, and L. Van Gool. Non-maximum suppression for object detection by passing messages between windows. In Asian Conference on Computer Vision, pages 290–306. Springer, 2014.

[3] D. Mrowca, M. Rohrbach, J. Hoffman, R. Hu, K. Saenko, and T. Darrell. Spatial semantic regularisation for large scale object detection. In Proceedings of the IEEE international conference on computer vision, pages 2003–2011, 2015. 

[4]     Soft-NMS --Improving Object Detection With One Line of Code  https://arxiv.org/abs/1704.04503 

[5]   Inception Single Shot MultiBox Detector for object detection https://ieeexplore.ieee.org/document/8026312/

[6]   Bounding Box Regression with Uncertainty for Accurate Object Detection https://arxiv.org/abs/1809.08545 

[7]   Acquisition of Localization Confidence for Accurate Object Detection https://arxiv.org/abs/1807.11590

[8] Adaptive NMS: Refining Pedestrian Detection in a Crowd https://arxiv.org/abs/1904.03629 

[9] YOLACT: Real-time Instance Segmentation https://arxiv.org/abs/1904.02689 

[10]     Enhancing Geometric Factors in Model Learning and Inference for Object Detection and Instance Segmentation https://arxiv.org/abs/2005.03572 

[11]     Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression https://arxiv.org/abs/1911.08287 

[12] Confluence: A Robust Non-IoU Alternative to Non-Maxima Suppression in Object Detection 2005.03572.pdf (arxiv.org)

[13] 一文打尽目标检测NMS——效率提升篇 - 知乎 (zhihu.com)