数学建模学习笔记（二）:非线性规划模型例题与灵敏度分析

---

前言

数学建模解决问题的过程一般分为五个步骤，称为五步方法，五个步骤如下：
（1）提出问题
（2）选择建模方法
（3）推导模型的数学表达式
（4）求解模型
（5）回答问题

---

一、一个简单的非线性规划模型

我们先来看如下的问题:
一家彩电制造商计划推出两种新产品:一种为19英寸液晶平板电视机，制造商建议零售价为339美元；另一种为21英寸液晶平板电视机，零售价为399美元。公司付出的成本为19英寸彩电每台195美元，21英寸彩电每台 225美元，还要加上400000美元的固定成本。在竞争的销售市场中，每年售出的彩电数量会影响彩电的平均售价。据统计，对每种类型的彩电，每多售出一台，平均销售价格会下降1美分。而且19英寸彩电的销售会影响21英寸彩电的销售，反之亦然。据估计，每售出一台21英寸彩电，19英寸彩电的平均售价会下降0.3美分，而每售出一台19英寸彩电，21英寸彩电的平均售价会下降0.4美分。问每种彩电应该生产各生产多少台。

二、问题的求解

1、模型的建立与求解

第一步，我们可以根据题目所给的信息列出一张变量表，然后写出这些变量间的关系及其他假设。最后采用符号语言将问题用数学公式表达。（表1）
$$\begin{array}{cl}& x_1=19英寸彩电每年的售出数量/台\\ & x_2=21英寸彩电每年的售出数理/台\\ & p_1=19英寸彩电的销售价格/美元\\ 变量& p_2=21英寸彩电的销售价格/美元\\ & c=生产彩电的成本/（美元/年）\\ & r=彩电销售的收入/（美元/年）\\ & f=彩电销售的利润/（美元/年）\\ & p_1=339-0.01x_1-0.03x_2\\ & p_2=399-0.004x_1-0.01x_2\\ 假设& c=400000+195x_1+225x_2\\ & r=p_1{x}_1+p_2{x}_2\\ & f=r-c\\ & x_1,x_2\ge 0\\ 目标& 求f的最大值\end{array}$$

第二步选择建模方法，我们可将上述问题视为无约束的多变量最优化问题。

第三步，根据第二步中选择的建模方法推导模型的公式。
$$\begin{array}{rl}f& =r-c\\ & =p_1{x}_1+p_2{x}_2-(400000+195x_1+225x_2)\\ & =(339-0.01x_1-0.003x_2)x_1+(399-0.004x_1-0.01x_2)x_2-(400000+195x_1+225x_2)\\ & =-0.01x_1^2-0.007x_1{x}_2-0.01x_2^2+144x_1+174x_2-400000\end{array}$$

令$y=f$为求最大值的目标函数，$x_1,x_2$为决策变量。
则问题转化为在区域
$$S=\{(x_1,x_2):x_1\ge 0,x_2\ge 0\}$$
求出
$$\begin{array}{r}y=f(x_1,x_2)=-0.01x_1^2-0.007x_1{x}_2-0.01x_2^2+144x_1+174x_2-400000\end{array}$$
的最大值。

第四步，求解模型。即对函数$f(x_1,x_2)$在(1)式定义的区域$S$上求最大时。下面我们给出函数$f$的三维图形,

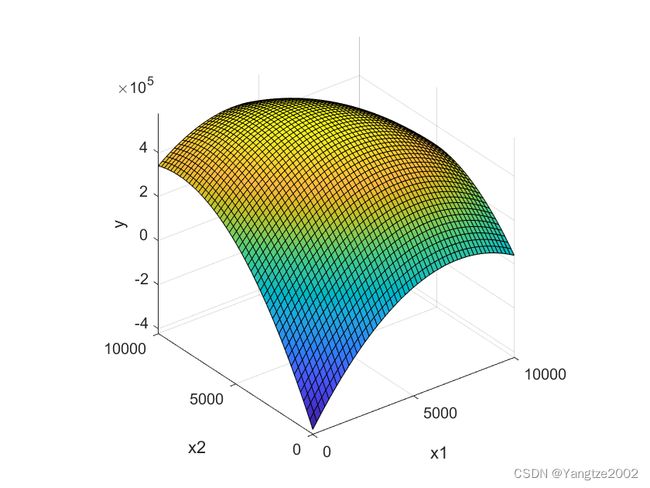
上图显示$f(x_1,x_2)$在S的内部达到最大值，下面是Matlab代码：

clc;clear;close all;
[x1,x2]=meshgrid(0:200:10000);%快速生成网格线
y=-0.01.*x1.^2-0.007.*x1.*x2-0.01.*x2.^2+144.*x1+174.*x2-400000;%定义函数
surf(x1,x2,y)%绘制曲面
xlabel('x1');ylabel('x2');zlabel('y');%加上坐标轴标签
axis vis3d%冻结屏幕高宽比

上图给出了$f(x_1,x_2)$的水平图集，从中可以估计出$f(x_1,x_2)$的最大值出现在$x_1=5000,x_2=7000$附近。下面是Matlab代码：

contourf(x1,x2,y,'ShowText','on')%作出彩色的等高线图，并显示数值
xlabel('x1');ylabel('x2');

函数$f$为抛物面，为求其最大值点，令$▽f=0$,得到方程组
$$\{\begin{array}{l}\frac{\partial f}{\partial x_1}=144-0.02x_1-0.007x_2=0\\ \frac{\partial f}{\partial x_2}=174-0.007x_1-0.02x_2=0\end{array}$$
求解上面方程组可以得到最优解$x_1=4735,x_2=7043$;目标函数的最大值$f=553641.025$

2、得出结论

经过上述分析，我们可以得出如下结论：这家公司可以通过生产4735台19英寸彩电和7043台21英寸彩电来获得最大利润。此时，每台19英寸的平均售价为270.52元，每台21英寸彩电的平均售价为309.63元。生产的总支出为2908000元，相应的利润率为19%。我们建议这家公司应该实行推出新产品的计划。

三、灵敏度分析

上面所得出的结论是以表1中所作的假设为基础的。实际中的生产过程会有一定的变化，因此我们可以对上述假设进行灵敏度分析，以保证结果具有稳定性。
我们主要关心的是决策变量$x_1和x_2$的值，不妨对19英寸彩电的价格弹性系数a的灵敏度进行分析。在模型中假设a=0.01美元/台。
将其带入前面的公式中，得出（式3-1）
$$y=f(x_1,x_2)=-a{x}_1^2-0.007x_1{x}_2-0.01x_2^2+144x_1+174x_2-400000$$
求偏导数并令其为零，
$$\{\begin{array}{l}\frac{\partial f}{\partial x_1}=144-2a{x}_1-0.007x_2=0\\ \frac{\partial f}{\partial x_2}=174-0.007x_1-0.02x_2=0\end{array}$$
求出其最优解（式3-2）
$$x_1=\frac{1662000}{40000a-49},x_2=\frac{48000(7250a-21)}{40000a-49}$$
下面分别给出$x_1,x_2$关于价格弹性系数a的曲线图,

附：

clc;clear;close all;
a=0:0.001:0.02;
x1=1662000./(40000.*a-49);
figure
plot(a,x1)
xlabel('a');
ylabel('x1');
xlim([0.002 0.02])%限制x轴显示范围

上图显示，19英寸彩电的价格弹性系数a的提高，会导致19英寸彩电的最有生产量$x_1$的下降，及21英寸彩电的最优生产量$x_2$的提高，且$x_1$比$x_2$对于a更敏感。这些都是合理的。
将灵敏性数据表示乘相对该变量或百分比改变的形式，如果$a$改变了$△a$,导致$x_1$有$△x_1$的改变量，则相对该变量的比值为$△x_1/x_1$与$△a/a$的比值。令$△a\to 0，$按照导数的定义，有
$$\frac{△x_1/x_1}{△a/a}\to \frac{\mathrm{d}{x}_1}{\mathrm{d}a}\cdot \frac{a}{x_1},$$
这个极限值称为$x_1$对$a$的灵敏性，记为$S(x_1,a)$。为得到这些灵敏性的具体数值，计算在$a=0.01$时，有
$${\frac{\mathrm{d}{x}_1}{\mathrm{d}a}|}_{a=0.01}=-539606,$$
因此
$$S(x_1,a)=\frac{\mathrm{d}{x}_1}{\mathrm{d}a}\cdot \frac{a}{x_1}=-539606\times \frac{0.01}{4735}\approx -1.1,$$
类似地可以计算出
$$S(x_2,a)=\frac{\mathrm{d}{x}_2}{\mathrm{d}a}\cdot \frac{a}{x_2}\approx 0.27$$
如果19英寸彩电的价格弹性系数a提高10%,即当a=0.011时，则应该将19英寸彩电的生产量缩小11%,将21英寸彩电的生产力扩大2.7%。
下面讨论y对于a的灵敏性。为得到y关于a的表达式，将式3-2代入y关于$x_1，x_2$的表达式中
$$y=f(a)=\frac{356900a^3+414.795a^2-2.6229669375a+0.00193460575}{(a-0.001225{)}^3}$$
下面给出y关于a的曲线图(如图)，可以看出，19英寸彩电的价格系数a的提高会导致利润的下降。

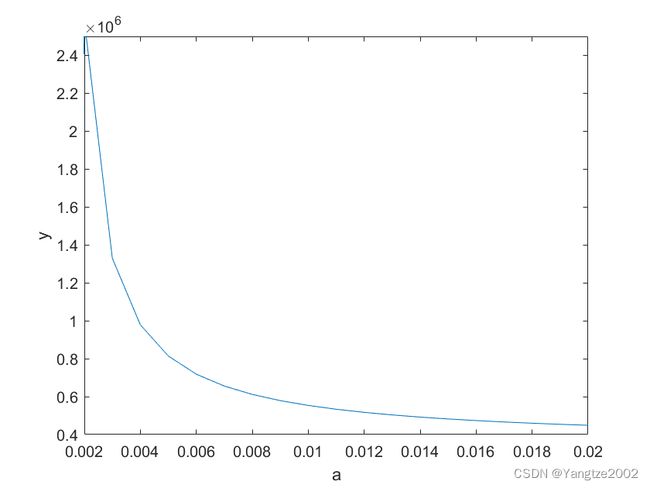
附：

clc;clear;close all;
a=0:0.001:0.02;
y=(356900.*a.^3+414.795.*a.^2-2.6229669375.*a+0.00193460575)./(a-0.001225).^3;
figure
plot(a,y)
xlabel('a');
ylabel('y');
xlim([0.002 0.02])
ylim([0.4*10^6 2.5*10^6])

为计算利润y关于a的灵敏性$S(y,a)$,要求出$\frac{\mathrm{d}y}{\mathrm{d}a}$，可以利用多变量函数的链式法则（式3-3）
$$\frac{\mathrm{d}y}{\mathrm{d}a}=\frac{\partial y}{\partial x_1}\cdot \frac{\mathrm{d}{x}_1}{\mathrm{d}a}+\frac{\partial y}{\partial x_2}\cdot \frac{\mathrm{d}{x}_2}{\mathrm{d}a}+\frac{\partial y}{\partial a}$$
由于在极值点$\frac{\partial y}{\partial x_1}$与$\frac{\partial y}{\partial x_2}$都为零，因此有
$$\frac{\mathrm{d}y}{\mathrm{d}a}=\frac{\partial y}{\partial a}=-x_1^2$$
由式3-1可直接得到
$$S(y,a)=\frac{\mathrm{d}y}{\mathrm{d}a}\cdot \frac{a}{y}=-x_1^2\frac{a}{y}=-4735^2\times \frac{0.01}{553641}\approx -0.40$$
因此，如果19英寸彩电的价格弹性系数a提高10%，会使利润下降4%。
式3-3中
$$\frac{\partial y}{\partial x_1}\cdot \frac{\mathrm{d}{x}_1}{\mathrm{d}a}+\frac{\partial y}{\partial x_2}\cdot \frac{\mathrm{d}{x}_2}{\mathrm{d}a}=0$$
导数$\frac{\mathrm{d}y}{\mathrm{d}a}$代表了最优生产量$x_1$和$x_2$的变化对利润的影响，其和为零说明了生产量的微小变化（至少在线性近似时）对利润没有影响。从几何上看，由于$y=f(x_1,x_2)$在极值点是平的，所以$x_1$和$x_2$的微笑变化对$y$几乎没有什么影响。由于19英寸彩电的价格弹性系数a提高10%而导致的最优利润的下降几乎全部是由售价的改变引起的，因此我们给出的生产量几乎最优的。
例如，设a=0.01,但假设实际的价格弹性系数比它高出了10%。用式3-2确定最优生产量，这意味着a=0.011时给出的最优解与原最优解相比，会多生产10%的19英寸彩电，少生产约3%的21英寸彩电，而且，利润也会比最优值低4%。但如果采用原模型的结果，a=0.011时仍按$x_1=4735,x_2=7043$确定生产量，会得到利润值为531221美元。而最优利润为533514美元。
因此，采用该模型的结果，虽然现在的生产量与最优的生产量有相当大的差距，但获得的利润仅仅比可能的最优利润损失了0.43%。在这一意义下，该模型显示了非常好的稳定性。

总结

以上就是关于该问题的模型求解及灵敏度分析的过程，由于博主仍在学习写作阶段，如有错误请大家指正，不胜感激！

参考书目

司守奎 孙玺菁《数学建模算法与应用》第3版