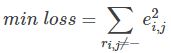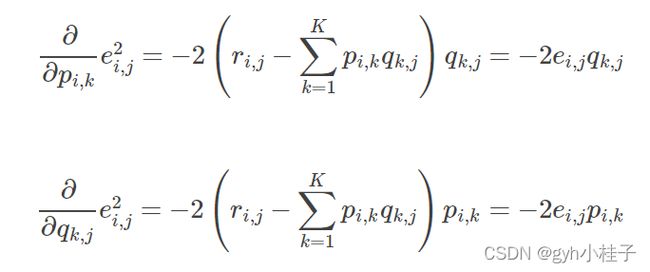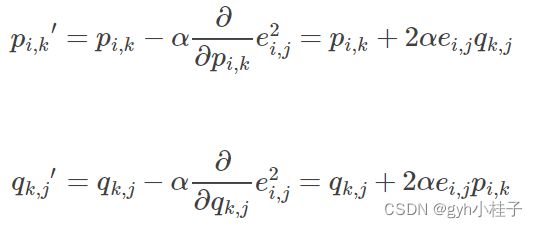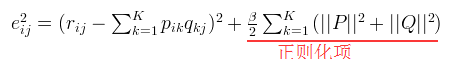矩阵分解及其代码实现

目录

1.问题引入

2.矩阵运算：

2.1矩阵相乘：

2.2矩阵转置 

2.3矩阵分解：

2.4 预测矩阵的表示：

3.损失函数：

 3.1. 首先

3.2如何构造损失函数

3.损失函数求解：

4.正则化：

5.python代码实现：

---

1.问题引入

     个人认为学习这个内容需要掌握四大块：1.掌握矩阵的一些运算，2.了解损失函数的意思，3.了解正则化，4，最后看懂代码，进行一定程度上的代码实现。 

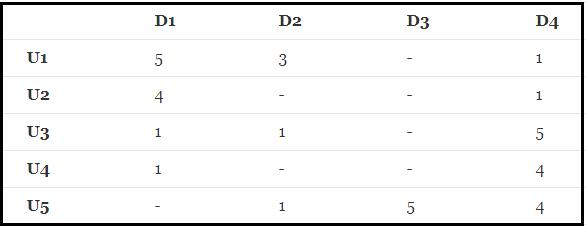
下面对矩阵分解的学习会用上面的图片 ，Ui代表不同的用户，Di代表不同的物品，下面的数字代表每个用户对每个物品的评分(假设满分为5分)。

2.矩阵运算：

2.1矩阵相乘：

 矩阵相乘的特点： 
（1）当矩阵A的列数等于矩阵B的行数时，A与B才可以相乘。 
（2）乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。 
（3）矩阵C的行数等于矩阵A的行数，C的列数等于B的列数

  若有一个矩阵R，矩阵R可以近似表示为P和Q的乘积，即：R（n,m）≈ P(n,K)*Q(K,m)

2.2矩阵转置 

把矩阵A的行换成同序数的列得到的新矩阵，叫做A的转置矩阵(Transpose of a Matrix)，记作ATAT。

因此，转置矩阵的特点： 
（1）转置矩阵的行数是原矩阵的列数，转置矩阵的列数是原矩阵的行数； 
（2）转置矩阵下标（i，j）的元素对应于原矩阵下标（j，i）的元素

2.3矩阵分解：

           矩阵分解的过程中，将原始矩阵

分解成两个矩阵

和

                                                                        

的乘积： 

2.4 预测矩阵的表示：

 在这个例子中我们将会用到矩阵分解和矩阵相乘

3.损失函数：

损失函数对我们来说并不陌生，我在线性回归的里面写到过这个内容，现在在写一遍：

损失函数定义:

    损失函数是机器学习里最基础也是最为关键的一个要素，通过对损失函数的定义、优化，就可以衍生到我们现在常用的机器学习等算法中。

  损失函数的作用：衡量模型模型预测的好坏。再简单一点说就是：损失函数就是用来表现预测与实际数据的差距程度。损失函数越小越好。

 3.1. 首先

3.2如何构造损失函数

我认为就是求出原来的值与预测的值的差，然后再进行平方。

 以上面的评分为例来说明：使用原有的评分矩阵Rm×n与重新构建的评分矩阵R^m×n进行相减求的误差的平方作为损失函数，即为

最后需要求的所有非负项的损失函数的最小值，在运用梯度下降算法时，也会用损失函数的值作为迭代的一个限制条件，还有一个限制条件就是迭代的次数(cnt)

3.损失函数求解：

对于损失函数求解我们可以利用梯度下降进行求导，对不同的变量进行求导，梯度下降法的核心步骤是：

• 求解损失函数的负梯度

因为e=

 所以：

• 根据负梯度的方向更新变量：

通过不断迭代，不断更新值,和,可以通过迭代次数和阈值作为限制条件

4.正则化：

    为了防止过拟合，增加正则化项。

加入正则化的损失函数求解：

4.1.第一步和没有使用正则化是一样的

4.2. 加入正则化后的损失函数为：

即：

4.3.使用梯度下降法获得修正的p和q分量：

• 　　求解损失函数的负梯度：

• 　　根据负梯度的方向更新变量：

然后就通过不断迭代以此来不断更新值，直到遇到限制条件。

预测

5.python代码实现：

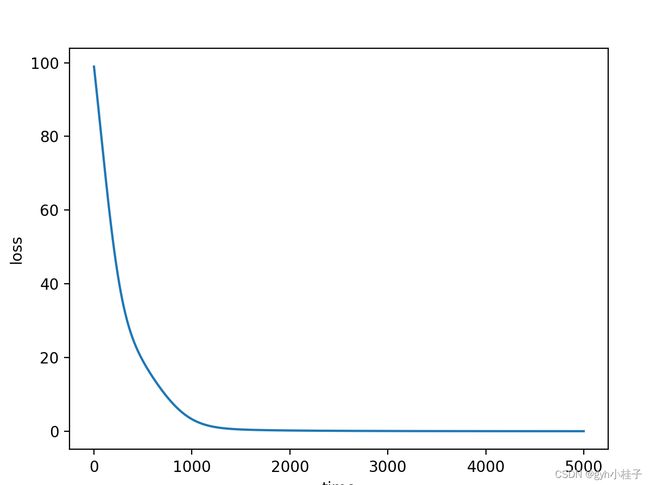
   加正则化：      其中矩阵Q是新生成的一个M行K列矩阵，矩阵P是N行K列的矩阵，之后传入函数defmatrix_factorization(R,P,Q,K,steps=5000,alpha=0.0002,beta=0.02):中，在函数里面，Q=Q.T是为了得到转置，这样Q就变成了K行M列，这样就可以与P进行相乘得到最后的预测结果。

from math import *
import numpy as np
import matplotlib.pyplot as plt
def matrix_factorization(R,P,Q,K,steps=5000,alpha=0.0002,beta=0.02): #矩阵因子分解函数，steps：梯度下降次数；alpha：步长；beta：β。
    Q=Q.T#新生成的Q的转置矩阵               # .T操作表示矩阵的转置
    result=[]#用于储存加入正则化后的损失函数求和后的值
    for step in range(steps): #梯度下降，steps迭代次数
        for i in range(len(R)):#len(R)代表矩阵的行数
            for j in range(len(R[i])):#取每一行的列数
                    eij=R[i][j]-np.dot(P[i,:],Q[:,j])       # .DOT表示矩阵相乘
                    for k in range(K):
                      if R[i][j]>0:        #限制评分大于零
                        P[i][k]=P[i][k]+alpha*(2*eij*Q[k][j]-beta*P[i][k])   #增加正则化，并对损失函数求导，然后更新变量P
                        Q[k][j]=Q[k][j]+alpha*(2*eij*P[i][k]-beta*Q[k][j])   #增加正则化，并对损失函数求导，然后更新变量Q
        eR=np.dot(P,Q)
        e=0#用来保存损失函数求和后的值
        for i in range(len(R)):#每一行循环
            for j in range(len(R[i])):#每一列循环
              if R[i][j]>0:
                    e=e+pow(R[i][j]-np.dot(P[i,:],Q[:,j]),2)      #损失函数求和
                    for k in range(K):
                        e=e+(beta/2)*(pow(P[i][k],2)+pow(Q[k][j],2)) #加入正则化后的损失函数求和
        result.append(e)
        if e<0.001:           #判断是否收敛，0.001为阈值
            break
    return P,Q.T,result

if __name__ == '__main__':   #主函数
    R=[                 #原始矩阵
        [5,3,0,1],
        [4,0,0,1],
        [1,1,0,5],
        [1,0,0,4],
        [0,1,5,4]
    ]
    R=np.array(R)
    N=len(R)    #原矩阵R的行数
    M=len(R[0]) #原矩阵R的列数
    K=3    #K值可根据需求改变
    P=np.random.rand(N,K) #随机生成一个 N行 K列的矩阵
    Q=np.random.rand(M,K) #随机生成一个 M行 K列的矩阵
    nP,nQ,result=matrix_factorization(R,P,Q,K)#nP=P，nQ=nQ.T,result=result
    print("输出原矩阵：")
    print(R)         #输出原矩阵
    R_MF=np.dot(nP,nQ.T)#矩阵的乘积
    print("输出新矩阵：")
    print(R_MF)      #输出新矩阵
    #画图
    plt.plot(range(len(result)),result)
    plt.xlabel("time")
    plt.ylabel("loss")
    plt.show()

输出结果：

输出原矩阵：
[[5 3 0 1]
 [4 0 0 1]
 [1 1 0 5]
 [1 0 0 4]
 [0 1 5 4]]
输出新矩阵：
[[4.98067845 2.9761162  2.84953808 1.00359896]
 [3.97858746 1.78290637 3.12381968 1.00229724]
 [1.00184528 0.9931711  2.78202187 4.97058181]
 [0.99909932 0.85761773 2.38753953 3.98254216]
 [3.32404613 1.00984832 4.98333193 3.98733355]]

 python画图：

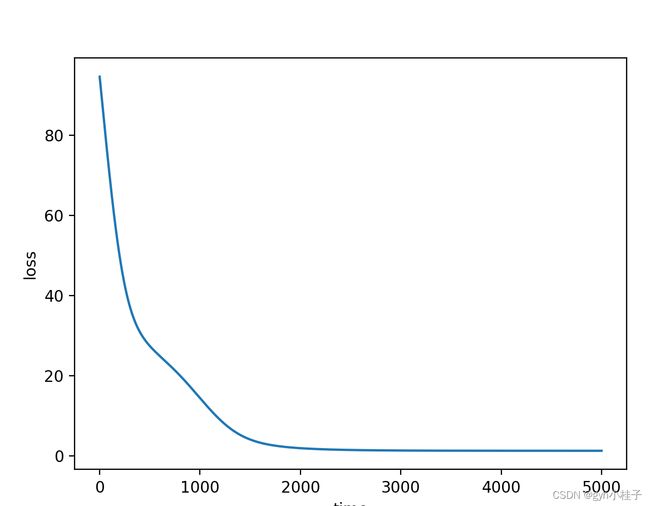
无正则化：在上面的基础上，通过修改写出未加入正则化的python代码：

from math import *
import numpy as np
import matplotlib.pyplot as plt
def matrix_factorization(R,P,Q,steps=5000,alpha=0.0002,beta=0.02): #矩阵因子分解函数，steps：梯度下降次数；alpha：步长；beta：β。
    Q=Q.T#新生成的Q的转置矩阵               # .T操作表示矩阵的转置
    result=[]#用于储存加入正则化后的损失函数求和后的值
    for step in range(steps): #梯度下降，steps迭代次数
        for i in range(len(R)):#len(R)代表矩阵的行数
            for j in range(len(R[i])):#取每一行的列数
                    eij=R[i][j]-np.dot(P[i,:],Q[:,j])       # .DOT表示矩阵相乘
                    for k in range(K):
                      if R[i][j]>0:        #限制评分大于零
                        P[i][k]=P[i][k]+alpha*2*eij*Q[k][j]  #没加入正则化，并对损失函数求导，然后更新变量P
                        Q[k][j]=Q[k][j]+alpha*2*eij*P[i][k]  #没加入正则化，并对损失函数求导，然后更新变量Q
        eR=np.dot(P,Q)
        e=0#用来保存损失函数求和后的值
        for i in range(len(R)):#每一行循环
            for j in range(len(R[i])):#每一列循环
              if R[i][j]>0:
                    e=e+pow(R[i][j]-np.dot(P[i,:],Q[:,j]),2)      #损失函数求和
        result.append(e)
        if e<0.001:           #判断是否收敛，0.001为阈值
            break
    return P,Q.T,result

if __name__ == '__main__':   #主函数
    R=[                 #原始矩阵
        [5,3,0,1],
        [4,0,0,1],
        [1,1,0,5],
        [1,0,0,4],
        [0,1,5,4]
    ]
    R=np.array(R)
    N=len(R)    #原矩阵R的行数
    M=len(R[0]) #原矩阵R的列数,在这里求列数和行数，是为了P和Q相乘后与原矩阵具有相同的行和列
    K=3
    P=np.random.rand(N,K) #随机生成一个 N行 K列的矩阵
    Q=np.random.rand(M,K) #随机生成一个 M行 K列的矩阵
    nP,nQ,result=matrix_factorization(R,P,Q)#nP=P，nQ=nQ.T,result=result
    print("输出原矩阵：")
    print(R)         #输出原矩阵
    R_MF=np.dot(nP,nQ.T)#矩阵的乘积
    print("输出新矩阵：")
    print(R_MF)      #输出新矩阵
    #画图
    plt.plot(range(len(result)),result)
    plt.xlabel("time")
    plt.ylabel("loss")
    plt.show()

 结果代码：

输出原矩阵：
[[5 3 0 1]
 [4 0 0 1]
 [1 1 0 5]
 [1 0 0 4]
 [0 1 5 4]]
输出新矩阵：
[[5.05012796 2.85469134 5.80052834 0.99533487]
 [3.95534029 2.22271651 4.66029473 0.99616947]
 [1.10372258 0.7124859  3.8909487  4.99555685]
 [0.94579615 0.6751661  3.18376022 3.99414936]
 [2.57938868 1.39377654 4.8865643  4.03595907]]

图示：