数据降维和特征选择

数据降维和特征选择

博主言：本文作为理论和概念整理，不做公式推导和详解计算过程，如需了解相关概念的计算公式和过程，在文后的参考链接中有详细的公式，计算过程和实例。

特征工程概述

特征工程的定义

特征工程是将原始数据转化为特征，更好表示预测模型处理的实际问题，提升对于未知数据的准确性。它是用目标问题所在的特定领域知识或者自动化的方法来生成、提取、删减或者组合变化得到特征。

特征工程的意义

1、数据特征会直接影响预测模型和实现的预测结果。
2、优质特征的灵活性可以让你使用简单的模型运算得更快，更容易理解，更容易维护。
3、优质的特征可以在使用不是最优的模型参数的情况下得到不错的预测结果。

迭代过程

1、 问题分析，观察数据
2、 特征设计
3、 特征选择
4、 评估模型

数据特征会直接影响预测模型和实现的预测结果。准备和选择的特征越好，则实现的结果越好。大多数模型都可以通过数据中良好的结构很好的学习，即使不是最优的模型，优质的特征也可以得到不错的效果。优质特征的灵活性可以让你使用简单的模型运算的更快，更容易理解，更容易维护。优质的特征可以在使用不是最优的模型参数的情况下得到不错的预测结果，这样你就不必费力去选择最适合的模型和最优的参数了。

数据降维之PCA

算法原理

通过协方差矩阵的特征值分解得到数据的主成分，发现特征之间的线性关系，并去除。通过协方差矩阵的特征值分解能够得到数据的主成分，以二维特征为例，两个特征之间可能存在线性关系（例如运动的时速和秒速度），这样就造成了第二维信息是冗余的。PCA的目标是发现这种特征之间的线性关系，并去除。

分类假设（只用于降维可以不考虑）

1. 数据结构都是线性的
2. 数据的概率分布满足高斯分布或指数型的概率分布

算法流程

1. 特征归一化
2. 计算协方差矩阵
3. 奇异值分解求特征值和特征向量
4. 选取降维个数

综述

1. 线性降维方法

2. 不建议使用PCA解决过拟合问题
   PCA是一种无监督学习，其存在的假设是：方差越大信息量越多。但是信息（方差）小的特征并不代表表对于分类没有意义，可能正是某些方差小的特征直接决定了分类结果，而PCA在降维过程中完全不考虑目标变量的做法会导致一些关键但方差小的分类信息被过滤掉。

3. PCA只应用到训练数据集
   直接使用所有的样本进行训练， 这样实际上相当于作弊的， 这样的话降维矩阵是在包含训练样本和测试样本的情况下训练得到的， 在进行测试的时候， 测试样本会存在很大的优越性， 因为它已经知道了要降维到的空间情况。

4. 一般在原数据集能跑出比较好的结果时使用PCA降维

数据降维之LDA

算法原理

基本思想是将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性

分类假设

(1) 样本数据是正态分布；
(2) 特征是随机独立的；
(3) 对于每个类别，具有一致的协方差矩阵；

维度

 PCA降维是直接和数据维度相关的，比如原始数据是n维的，那么PCA后，可以任意选取1维、2维，一直到n维都行（当然是对应特征值大的那些）。LDA 降维是直接和类别的个数相关的，与数据本身的维度没关系，比如原始数据是n维的，一共有C个类别，那么LDA降维之后，一般就是1维，2维到C-1维进行选择

PCA与LDA比较

PCA目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以此使用较少的数据维度，同时保留住较多的原数据点的特性。

PCA追求的是在降维之后能够最大化保持数据的内在信息，并通过衡量在投影方向上的数据方差的大小来衡量该方向的重要性。但是这样投影以后对数据 的区分作用并不大，反而可能使得数据点揉杂在一起无法区分。如右图，若使用PCA将数据点投影至一维空间上时，PCA会选择2轴，这使得原本很容易区分的两簇点被揉杂在一起变得无法区分。

PCA主要是从特征的协方差角度，去找到比较好的投影方式。LDA更多的是考虑了标注，即希望投影后不同类别之间数据点的距离更大，同一类别的数据点更紧凑。所以在右图中LDA会选择投影到1轴。所以如果算法用于分类，则LDA更具有优越性。

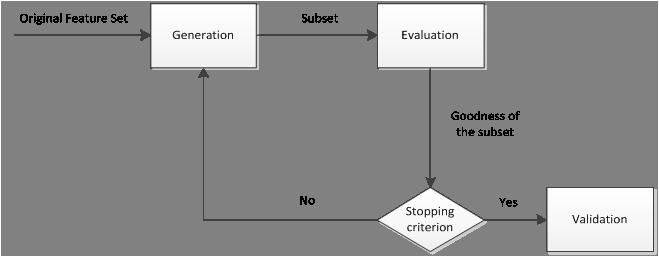
特征选择

特征选择的目标是寻找最优特征子集。特征选择能剔除不相关(irrelevant)或冗余(redundant )的特征，从而达到减少特征个数，提高模型精确度，减少运行时间的目的。另一方面，选取出真正相关的特征简化模型，协助理解数据产生的过程。

过滤式特征选择

过滤式特征选择的评价标准从数据集本身的内在性质获得，与特定的学习算法无关，因此具有较好的通用性。通常选择和类别相关度大的特征或者特征子集。相关度较大的特征或者特征子集会在分类器上可以获得较高的准确率。过滤式特征选择的评价标准分为四种，即距离度量、信息度量、关联度度量以及一致性度量

方差选择法

使用方差选择法，先要计算各个特征的方差，然后根据阈值，选择方差大于阈值的特征。

皮尔逊相关

皮尔逊相关统计或皮尔逊相关系数在统计模型中也称为 r 值。对于任何两个变量，它返回一个指示相关强度的值。

皮尔逊相关系数的计算方法为两个变量的协方差除以其标准方差的积。两个变量的规模变化不影响该系数。两个变量之间的相关系数越高，从一个变量去预测另一个变量的精确度就越高，这是因为相关系数越高，就意味着这两个变量的共变部分越多，所以从其中一个变量的变化就可越多地获知另一个变量的变化。

皮尔逊系数=（x和y的协方差）/x的标准差*y的标准差

皮尔逊相关适用条件：
(1)、两个变量之间是线性关系，都是连续数据。
(2)、两个变量的总体是正态分布，或接近正态的单峰分布。
(3)、两个变量的观测值是成对的，每对观测值之间相互独立

互信息相关

互信息评分法可以测量变量的分布，有助于减少其他变量值的不确定性。互信息评分可以最大化联合分布与包含多个维度的数据集中的目标变量之间的互信息。互信息度量 X 和 Y 共享的信息：它度量知道这两个变量其中一个，对另一个不确定度减少的程度。例如，如果 X 和 Y 相互独立，则知道 X 不对 Y 提供任何信息，反之亦然，所以它们的互信息为零。在另一个极端，如果 X 是 Y 的一个确定性函数，且 Y 也是 X 的一个确定性函数，那么传递的所有信息被 X 和 Y 共享：知道 X 决定 Y 的值，反之亦然。

常用互信息作为特征词和类别之间的测度，如果特征词属于该类的话，它们的互信息量最大。由于该方法不需要对特征词和类别之间关系的性质作任何假设，因此非常适合于文本分类的特征和类别的配准工作。

卡方检测

卡方检验最基本的思想就是通过观察实际值与理论值的偏差来确定理论的正确与否。具体做的时候常常先假设两个变量确实是独立的（行话就叫做“原假设”），然后观察实际值（也可以叫做观察值）与理论值（这个理论值是指“如果两者确实独立”的情况下应该有的值）的偏差程度，如果偏差足够小，我们就认为误差是很自然的样本误差，是测量手段不够精确导致或者偶然发生的，两者确确实实是独立的，此时就接受原假设；如果偏差大到一定程度，使得这样的误差不太可能是偶然产生或者测量不精确所致，我们就认为两者实际上是相关的，即否定原假设，而接受备择假设。

卡方检测与互信息

卡方检验对于出现次数较少的特征更容易给出高分。例如某一个特征就出现过一次在分类正确的数据中，则该特征会得到相对高的分数，而互信息则给分较低。其主要原因还是由于互信息在外部乘上了一个该类型出现的概率值，从而打压了出现较少特征的分数。 


另外这两种特征选择主要用于文本的分类等用监督学习，而不适宜聚类等无监督学习，因为聚类我们不知道每篇文档属于的类别，也就无从计算互信息和卡方值，这时一般使用TF-IDF作为特征词的选取方法

其他相关
肯德尔相关和斯皮尔曼相关
用于分类变量的数据或变量值的分布明显非正态或分布不明，计算时先对离散数据进行排序。与皮尔逊系数相同，都是求变量之间的线性关系。

基于计数
基于计数的特征选择是查找有关预测值的信息的简单而相对强大的方法。这是一种无监管的特征选择法，意味着你不需要标签列。此方法将统计所有值的频率，然后基于频率计数向列分配评分。它可用来在特定特征中查找信息的权重，并减少数据的维数，而不会丢失信息。

封装式特征选择

完全搜索

完全搜索分为穷举搜索(Exhaustive)与非穷举搜索(Non-Exhaustive)两类。

(1) 广度优先搜索( Breadth First Search )
算法描述：广度优先遍历特征子空间。
算法评价：枚举了所有的特征组合，属于穷举搜索，时间复杂度是O(2n)，实用性不高。

(2)分支限界搜索( Branch and Bound )
算法描述：在穷举搜索的基础上加入分支限界。例如：若断定某些分支不可能搜索出比当前找到的最优解更优的解，则可以剪掉这些分支。

(3) 定向搜索 (Beam Search )
算法描述：首先选择N个得分最高的特征作为特征子集，将其加入一个限制最大长度的优先队列，每次从队列中取出得分最高的子集，然后穷举向该子集加入1个特征后产生的所有特征集，将这些特征集加入队列。

(4) 最优优先搜索 ( Best First Search )
算法描述：与定向搜索类似，唯一的不同点是不限制优先队列的长度。

启发式搜索

(1)序列前向选择( SFS , Sequential Forward Selection )

算法描述：特征子集X从空集开始，每次选择一个特征x加入特征子集X，使得特征函数J( X)最优。简单说就是，每次都选择一个使得评价函数的取值达到最优的特征加入，其实就是一种简单的贪心算法。

算法评价：缺点是只能加入特征而不能去除特征。例如：特征A完全依赖于特征B与C，可以认为如果加入了特征B与C则A就是多余的。假设序列前向选择算法首先将A加入特征集，然后又将B与C加入，那么特征子集中就包含了多余的特征A。

(2)序列后向选择( SBS , Sequential Backward Selection )

算法描述：从特征全集O开始，每次从特征集O中剔除一个特征x，使得剔除特征x后评价函数值达到最优。

算法评价：序列后向选择与序列前向选择正好相反，它的缺点是特征只能去除不能加入。另外，SFS与SBS都属于贪心算法，容易陷入局部最优值。

(3) 双向搜索( BDS , Bidirectional Search )

算法描述：使用序列前向选择(SFS)从空集开始，同时使用序列后向选择(SBS)从全集开始搜索，当两者搜索到一个相同的特征子集C时停止搜索。

(4) 增L去R选择算法 ( LRS , Plus-L Minus-R Selection )

　　该算法有两种形式:
　　　　<1> 算法从空集开始，每轮先加入L个特征，然后从中去除R个特征，使得评价函数值最优。( L > R )
　　　　<2> 算法从全集开始，每轮先去除R个特征，然后加入L个特征，使得评价函数值最优。( L < R )
算法评价：增L去R选择算法结合了序列前向选择与序列后向选择思想， L与R的选择是算法的关键。

随机搜索

(1) 随机产生序列选择算法(RGSS, Random Generation plus Sequential Selection)

算法描述：随机产生一个特征子集，然后在该子集上执行SFS与SBS算法。
算法评价：可作为SFS与SBS的补充，用于跳出局部最优值。

(2) 模拟退火算法( SA, Simulated Annealing )

算法评价：模拟退火一定程度克服了序列搜索算法容易陷入局部最优值的缺点，但是若最优解的区域太小，则模拟退火难以求解。

(3) 遗传算法( GA, Genetic Algorithms )

算法描述：首先随机产生一批特征子集，并用评价函数给这些特征子集评分，然后通过交叉、突变等操作繁殖出下一代的特征子集，并且评分越高的特征子集被选中参加繁殖的概率越高。这样经过N代的繁殖和优胜劣汰后，种群中就可能产生了评价函数值最高的特征子集。

随机算法的共同缺点：依赖于随机因素，有实验结果难以重现。

嵌入式特征选择

在嵌入式特征选择中，特征选择算法本身作为组成部分嵌入到学习算法里。最典型的即决策树算法，如ID3、C4.5以及CART算法等，决策树算法在树增长过程的每个递归步都必须选择一个特征，将样本集划分成较小的子集，选择特征的依据通常是划分后子节点的纯度，划分后子节点越纯，则说明划分效果越好，可见决策树生成的过程也就是特征选择的过程。

信息熵

信息熵是用来衡量一个随机变量出现的期望值，一个变量的信息熵越大，那么他出现的各种情况也就越多，也就是包含的内容多，我们要描述他就需要付出更多的表达才可以，也就是需要更多的信息才能确定这个变量。

经验条件熵

假设将训练数据D按属性A进行划分，则按A属性进行分裂出的v个子集（即树中的v个分支），这些子集按目标类别进行分类所对应的熵的期望

信息增益

信息增益是针对一个一个的特征而言的，就是看一个特征t，系统有它和没它的时候信息量各是多少，两者的差值就是这个特征给系统带来的信息量，

信息增益度量的是：信息熵的降低量，这个降低是经过某个属性对原数据进行划分得出的。信息熵的降低，即确定性的提高，进一步讲，就是类别的数量在下降，那么确定为哪一类的可能性就提高，这样就更容易分类了。ID3算法就是基于信息增益来衡量属性（即特征）划分数据的能力，进而为特征（即属性）选择提供原则。

算法比较

ID3算法：

以信息增益为准则选择信息增益最大的属性。缺点：

1）信息增益对可取值数目较多的属性有所偏好，比如通过ID号可将每个样本分成一类，但是没有意义。
2）ID3只能对离散属性的数据集构造决策树。

鉴于以上缺点，后来出现了C4.5算法。

C4.5算法：

以信息增益率为准则选择属性；在信息增益的基础上对属性有一个惩罚，抑制可取值较多的属性，增强泛化性能。
其他优点：
2）能够对连续属性进行离散化处理（二分法）；
3）能够对缺失值进行处理；

缺点：构造树的过程需要对数据集进行多次顺序扫描和排序，导致算法低效；
解决方法：先从候选属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。而不是直接选择信息增益率最高的属性！

CART算法

顾名思义，可以进行分类和回归，可以处理离散属性，也可以处理连续的。分类树使用GINI指数来选择划分属性：在所有候选属性中，选择划分后GINI指数最小的属性作为优先划分属性。回归树就用最小平方差。

参考链接

特征工程与sklearn http://www.cnblogs.com/jasonfreak/p/5448385.html
特征工程 http://www.jianshu.com/p/ab697790090f
LDA算法 http://www.cnblogs.com/jerrylead/archive/2011/04/21/2024384.html
决策树 http://blog.csdn.net/you1314520me/article/details/45372201
封装式特征选择 http://www.cnblogs.com/heaad/archive/2011/01/02/1924088.html
卡方检测 http://www.xuebuyuan.com/1528910.html
互信息 http://www.cnblogs.com/gatherstars/p/6004075.html
皮尔逊相关系数 https://www.zhihu.com/question/19734616?sort=created
parzen窗概率密度函数估计 http://blog.sina.com.cn/s/blog_679e13290101cpr1.html