CartPole-v1线性模型局限

CartPole-v1线性模型局限 - 神经元非线性能力

背景

上篇文章有尝试使用最简单的单一神经元来解决CartPole-v1问题，模型比较简单，但是会存在两个比较明显的问题。

针对 问题2 大部分回合500，但是后期仍会出现回报较低的情况，最近几天学习了一些资料，这篇文章尝试着从数学的角度对其做一个解释。

从仿射函数说起

这里直接一点，先给出仿射函数(affine function)的公式：

$a=b+{\Sigma }_{i=1}^n{w}_i{x}_i$

下面是神经元的计算公式：

$z=wx+b$
$a=\sigma (z)$

可以看出，神经元实际上就是仿射函数和激活函数组成的复合函数。

仿射函数的计算表示

这里我们拿到向量的维度里来描述仿射函数。形式上，向量的内积跟去掉偏置(bias)的向量内积在形式上是等价的。

假设$x,y$为$n$维向量，向量内积计算公式：

<$x,y$> $=x_1{y}_1+x_2{y}_2+...+x_n{y}_n={\Sigma }_{i=1}^n{x}_i{y}_i$

向量内积的数学意义

定义向量的模表示为$||x||$为$x$与它自身内积的平方根。

$||x||=\sqrt{<x,x>}=\sqrt{{\Sigma }_{i=1}^n{x}_i^2}$

根据毕达哥拉斯定理（勾股定理），我们很容易得出，$x$ 的模即为$x$向量的长度。

两向量$x$，$y$组成的三角形，第三边可表示为$y-x$，如下图所示。

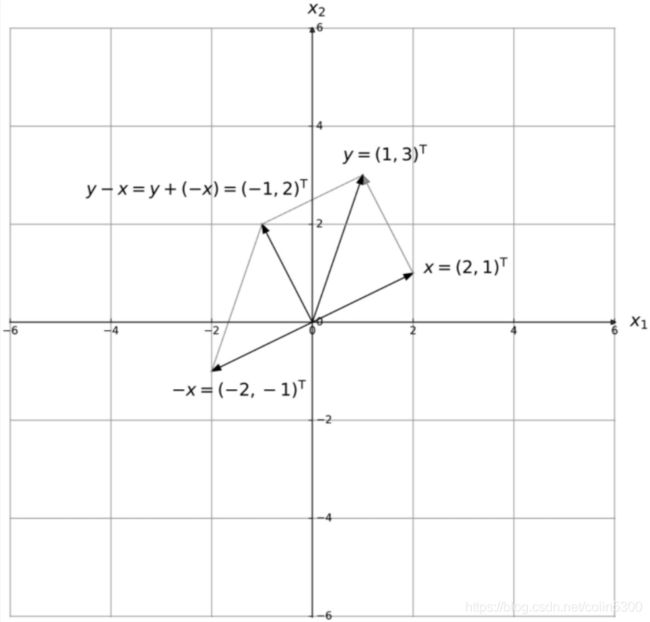
这里考虑二维向量，套用三角形三边公式

$c^2=a^2+b^2-2abcos\theta$

可得

$||y-x|{|}^2=||x|{|}^2+||y|{|}^2-2||x||||y||cos\theta$

化简后可得到

$<x,y>=||x||||y||cos\theta$

即，$x$与$y$的内积，等于$y$的模与$x$在$y$上的投影长度之积（$x$、$y$可互换），如下图，结论可推广到多维。

回到最开始的问题，关于$x$的仿射函数，即为$x$在其权重向量$w$上的投影长度与$w$模的乘积，再加上偏置$b$。

信息丢失问题

我们再思考下权重$w$，它是agent在学习过程中不断调整的一个向量。但从本质上来说，$w$是一个常量。什么意思呢，学习结束后，它是一个不变的值。

那上面 “$x$在其权重向量$w$上的投影长度与$w$模的乘积，再加上偏置$b$” 的结果，抛去$b$不讨论，则只取决于$x$在$w$上的投影长度。

这里有两点值得注意：

1. 在垂直于$w$的某条直线上，所有的$x$都具有相同的结果，这里垂直于$w$方向上的信息就丢失了
2. 这条垂直线是一条直线，直线上$x$的各个分量是线性相关的，$x_1$增加$\Delta x_1$，$x_2$就会增加$\alpha \Delta x_2$

第1点导致这个模型能解决的问题非常单一，形象点说，它会训练出二维平面里的一条线，或三维平面里的一个面来切分样本，判定其属于正类或负类。它没有非线性能力，不能切分如下的数据。

第二点，回到之前的CartPole-v1问题，这意味着，我们默认角度与角速度变化量的关系是等比例的。显然这是错误的。实际上同样是$30^o$角的变化，在垂直方向和稍微倾斜一点的方向上，产生的效果都是不同的。

总结

这个模型的缺陷已经很明确了。

因为CartPole-v1中，每一个观察到的参数都是单调的，所以使用单个神经元可以在很短的尝试次数收敛（基于一两次）；但这里的收敛并非真正的收敛，只是刚好找到一组对大部分样本都有效的线性模型。

线性模型只能拟合大部分场景，遇到一些特殊的点就失效了。比作一座山，我们能正常处理山腰以下的样本，山顶附近就会造成错误，快速失败。

那怎么去优化呢？这里最主要的还是需要让模型具备非线性能力，最显见的做法是，增加神经网络的层数，调整上层激活函数。

嗯，还需要再学习一下。