如何使用Python构建自己的MuZero AI
如何使用Python构建自己的MuZero AI
作者:David Foster
发表时间:2019年12月2日
原文连接:
MuZero: The Walkthrough(Part1/3),https://medium.com/applied-data-science/how-to-build-your-own-muzero-in-python-f77d5718061a
MuZero: The Walkthrough(Part2/3),https://medium.com/applied-data-science/how-to-build-your-own-deepmind-muzero-in-python-part-2-3-f99dad7a7ad
MuZero: The Walkthrough(Part3/3),https://medium.com/applied-data-science/how-to-build-your-own-deepmind-muzero-in-python-part-3-3-ccea6b03538b

如果你想了解最复杂的人工智能系统是如何工作的,那么,你来对地方了!
在这篇由三部分组成的系列中(翻译后合并为一个长篇),我们将探讨DeepMind发布的MuZero模型内部工作机制,MuZero是AlphaZero年轻的弟弟,但甚至更令人印象深刻。
还可以查看我的最新帖子,关于如何训练多人棋盘游戏的强化学习智能体,使用自我对弈!
我们将研究一下MuZero论文附带的伪代码——所以,沏一杯茶,找张舒服的椅子,开始吧。
α \alpha α
到目前为止的故事…
2019年11月19日,DeepMind向全球发布了最新的基于模型的强化学习算法——MuZero(译者:2012年12月23日,论文被《自然》收录)。
从2016年的AlphaGo论文开始,这已经是DeepMind深度强化学习不断突破的一系列论文中的第四篇。
要阅读从AlphaGo到AlphaZero的全部历史,请查看我以前的博客。
AlphaZero被誉为是一种通用的算法,它可以在没有任何人类专家先验知识的情况下快速地做好某件事。
那么,现在呢?
μ \mu μ
MuZero:用学习模型规划玩转雅达利、围棋、国际象棋和日本将棋。
MuZero跨出了终极的一步,MuZero拒不接受人类玩家的策略,甚至也不接受游戏规则。
换句话说,对于国际象棋,AlphaZero面对的挑战是:
学习如何自己与自己玩好这个游戏,这里有规则手册,解释每个棋子如何移动,哪些移动是合法的。它还告诉你如何判断一个棋局已经被将死(或者是平局)。
而MuZero面对的挑战是:
学会如何自己与自己玩好这个游戏,我会告诉你当前棋局什么动作是合规的,什么时候某一方赢了(或是平局),但我不会告诉你游戏中的整体规则。
因此,除了制定能赢的策略,MuZero还必须开发自己的的环境动力学模型,以便能够理解其选择的含义和未来规划。
想象一下,在一场从未被提前告知规则的比赛中,你试图玩得比世界冠军更好。MuZero恰恰做到了这一点!
在这篇文章中,我们将详细介绍MuZero是如何实现这个惊人壮举的。
MuZero伪代码
随MuZero论文,DeepMind还发布了Python伪代码,详细描述了算法每个部分之间的相互作用关系。
在本文中,我们将把其中的类和函数掰开了揉碎了,按逻辑摆放,并解释每个部分的功能和原理。我们假设MuZero正在学习下国际象棋,但这个过程对于任何游戏起始都一样,只是参数不同而已。全部伪代码都来自DeepMind开源伪代码。
让我们从对整个过程的描述开始,起点是入口函数muzero。
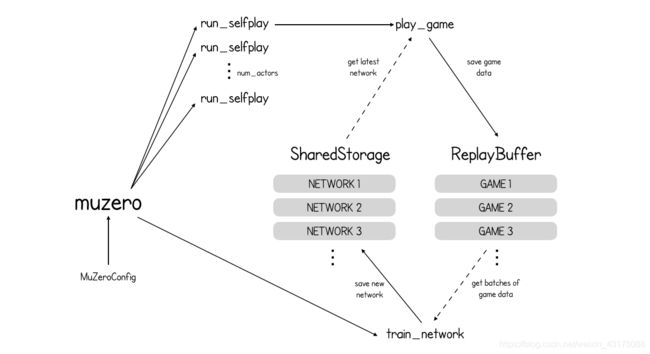
MuZero自我博弈(self-play)和训练(training)过程概述
def muzero(config: MuZeroConfig):
storage = SharedStorage()
replay_buffer = ReplayBuffer(config)
for _ in range(config.num_actors):
launch_job(run_selfplay, config, storage, replay_buffer)
train_network(config, storage, replay_buffer)
return storage.latest_network()
入口函数muzero的参数是一个MuZeroConfig对象,该对象存放了重要的运行参数,例如action_space_size和num_actors(要同时启动的游戏总数)。在其它函数中遇到这些参数时,我们再详细地介绍它们。
在较高的层次上,MuZero算法有两个独立的部分:自我博弈self-play(创建游戏数据)和训练training(不断改进神经网络)。算法的这两个部分都可以访问SharedStorage和ReplayBuffer对象,并分别保存神经网络和游戏数据。
共享存储和回放缓冲区
SharedStorage对象包含用于保存神经网络和从存储中获取最新神经网络的方法。
class SharedStorage(object):
def __init__(self):
self._networks = {}
def latest_network(self) -> Network:
if self._networks:
return self._networks[max(self._networks.keys())]
else:
# policy -> uniform, value -> 0, reward -> 0
return make_uniform_network()
def save_network(self, step: int, network: Network):
self._networks[step] = network
我们还需要一个ReplayBuffer来存储生成的游戏数据。其形式如下:
class ReplayBuffer(object):
def __init__(self, config: MuZeroConfig):
self.window_size = config.window_size
self.batch_size = config.batch_size
self.buffer = []
def save_game(self, game):
if len(self.buffer) > self.window_size:
self.buffer.pop(0)
self.buffer.append(game)
...
注意window_size参数是回放缓冲区中能保存的游戏最大数量。在MuZero中,设置为最近生成的1,000,000个游戏。
自我博弈(self-play)
在创建了共享存储和回放缓冲区之后,MuZero启动了num_actors个独立运行的并行游戏环境。国际象棋的num_actors设为3000。每个游戏环境都运行一个函数run_selfplay,从共享存储中取出最新版本网络参数,用它玩游戏play_game,并将游戏数据保存到回放缓冲区。
# Each self-play job is independent of all others; it takes the latest network
# snapshot, produces a game and makes it available to the training job by
# writing it to a shared replay buffer.
def run_selfplay(config: MuZeroConfig, storage: SharedStorage, replay_buffer: ReplayBuffer):
while True:
network = storage.latest_network()
game = play_game(config, network)
replay_buffer.save_game(game)
总之,MuZero不停地进行着成千上万次游戏,将这些游戏保存到一个回放缓冲区,然后根据这些游戏数据不断地训练自己。到目前为止,这与AlphaZero没什么不同。
我们将讨论AlphaZero和MuZero之间的关键区别——为什么MuZero有三个神经网络,而AlphaZero只有一个?
MuZero的3个神经网络
AlphaZero和MuZero都采用一种称为蒙特卡罗树搜索(MCTS)的技术来选择下一步动作的最佳方案。
这个想法是:为了选择下一步动作的最佳方案,就要“播放”从当前位置到未来可能出现的各种场景,然后用神经网络评估它们的价值,并选择未来预期价值最大化的动作。这似乎是我们人类下棋时脑子里面想的事,人工智能体也设计成利用这个技巧。
但是,这里有个问题,MuZero并不知道游戏规则,也就无从知晓一个给定的动作会如何影响游戏状态,所以它无法想象未来MCTS中的场景。它甚至不知道如何从给定的棋局中判断出下一步哪些动作是合法的,或者哪一方赢了。
MuZero论文中惊人的进展就是证明了这并不是问题。MuZero在自己的想象中创建了一个环境动力学模型,并在这个模型中进行优化学习如何玩游戏。
下图显示了AlphaZero和MuZero中MCTS进程之间的比较:
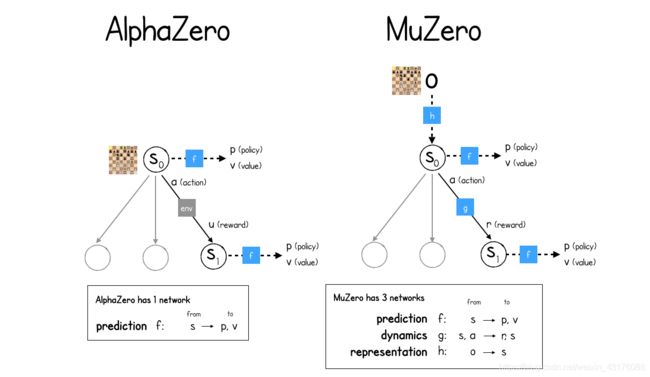
AlphaZero只有一个神经网络(预测predict),而MuZero则需要三个神经网络(预测predict、动力学dynamics、表征representation)
AlphaZero 预测(predict) 神经网络f的工作是预测给定游戏状态下的策略p和价值v。该策略p是全部动作的概率分布,价值v是对未来奖励估计的单一数值。每次MCTS走到一个未探测的叶节点时,都会进行这种预测,这样就可以立即为新棋局分配一个估计价值,并为后续每个动作分配概率。这些值被反向写到树上,直到根节点,这样经过多次模拟,在探索了大量未来不同可能性之后,根节点对当前状态下未来价值变得胸有成竹。
MuZero同样有一个 预测(predict) 神经网络f,但它所依据的“游戏状态”是一个隐藏表征,MuZero学习如何通过 动力学(dynamics) 神经网络g生成隐藏表征。动力学网络获取当前隐藏状态s和动作a,输出奖励r和新状态。注意,在AlphaZero中,MCTS树的状态转移是向环境要;而MuZero没那么奢侈,所以需要建立自己的的环境动力学模型!
最后,为了将当前观测到的游戏状态映射到初始表征,MuZero使用了第三种**表征(representation)**神经网络h。
因此,MuZero需要两个推理函数,以便通过MCTS树进行预测:
-
initial_inference为当前状态的初始推理,也就是h(表征)后面接f(预测)。 -
recurrent_inference为沿着MCTS树,在状态之间转移的递归推演,g(动力学)后接f(预测)。
虽然伪代码中没有提供精确的模型,但论文中给出了详细的描述。
class NetworkOutput(typing.NamedTuple):
value: float
reward: float
policy_logits: Dict[Action, float]
hidden_state: List[float]
class Network(object):
def initial_inference(self, image) -> NetworkOutput:
# representation + prediction function
return NetworkOutput(0, 0, {}, [])
def recurrent_inference(self, hidden_state, action) -> NetworkOutput:
# dynamics + prediction function
return NetworkOutput(0, 0, {}, [])
def get_weights(self):
# Returns the weights of this network.
return []
def training_steps(self) -> int:
# How many steps / batches the network has been trained for.
return 0
总之,在缺乏国际象棋真实规则的情况下,MuZero在头脑中创建了一个新游戏,并且可以控制和规划未来。这三个网络(预测、动力学和表征)一起优化,使得最终在想象环境中表现良好的策略,在真实环境中也能表现良好。
简直太棒了!
下面,我们将分析一下play_game函数,看看MuZero是如何决策在每个回合做出下一最佳动作的。
与MuZero玩游戏(play_game)
我们现在将仔细看一下play_game功能:
# Each game is produced by starting at the initial board position, then
# repeatedly executing a Monte Carlo Tree Search to generate moves until the end
# of the game is reached.
def play_game(config: MuZeroConfig, network: Network) -> Game:
game = config.new_game()
while not game.terminal() and len(game.history) < config.max_moves:
# At the root of the search tree we use the representation function to
# obtain a hidden state given the current observation.
root = Node(0)
current_observation = game.make_image(-1)
expand_node(root, game.to_play(), game.legal_actions(), network.initial_inference(current_observation))
add_exploration_noise(config, root)
# We then run a Monte Carlo Tree Search using only action sequences and the
# model learned by the network.
run_mcts(config, root, game.action_history(), network)
action = select_action(config, len(game.history), root, network)
game.apply(action)
game.store_search_statistics(root)
return game
首先,创建一个新的游戏对象并启动游戏主循环。当结束条件满足或游戏步数超过最大限制时,游戏结束。
我们从根节点开始进行蒙特卡洛树搜索(MCTS)。
root = Node(0)
每个节点都会保存一些关键的统计信息,这些统计信息包括:访问次数visit_count、轮到谁玩to_play、预测选择此节点动作的先验概率prior、节点的回填价值之和value_sum、子节点children、对应的隐藏状态hidden_state,以及从父节点转移到该节点预计能收到的奖励reward。
class Node(object):
def __init__(self, prior: float):
self.visit_count = 0
self.to_play = -1
self.prior = prior
self.value_sum = 0
self.children = {}
self.hidden_state = None
self.reward = 0
def expanded(self) -> bool:
return len(self.children) > 0
def value(self) -> float:
if self.visit_count == 0:
return 0
return self.value_sum / self.visit_count
再回到play_game,获取游戏对象返回的当前观测值(对应于上图中的o)…
current_observation = game.make_image(-1)
…并使用游戏提供的已知合规动作和当前观测值的推理来扩展根节点,当前观测值的推理由initial_inference函数提供。
expand_node(root, game.to_play(), game.legal_actions(),
network.initial_inference(current_observation))
# We expand a node using the value, reward and policy prediction obtained from
# the neural network.
def expand_node(node: Node, to_play: Player, actions: List[Action],
network_output: NetworkOutput):
node.to_play = to_play
node.hidden_state = network_output.hidden_state
node.reward = network_output.reward
policy = {a: math.exp(network_output.policy_logits[a]) for a in actions}
policy_sum = sum(policy.values())
for action, p in policy.items():
node.children[action] = Node(p / policy_sum)
我们还需要向根节点添加探索噪声,这一点非常重要,是为了确保MCTS探索一系列可能的动作而不仅仅探索当前被认为是最佳的动作。对于象棋,root_dirichlet_alpha= 0.3。
add_exploration_noise(config, root)
# At the start of each search, we add dirichlet noise to the prior of the root
# to encourage the search to explore new actions.
def add_exploration_noise(config: MuZeroConfig, node: Node):
actions = list(node.children.keys())
noise = numpy.random.dirichlet([config.root_dirichlet_alpha] * len(actions))
frac = config.root_exploration_fraction
for a, n in zip(actions, noise):
node.children[a].prior = node.children[a].prior * (1 - frac) + n * frac
下面,我们重点看MCTS过程。
run_mcts(config, root, game.action_history(), network)
MuZero中的montecarlo搜索树(run_mcts)
# Core Monte Carlo Tree Search algorithm.
# To decide on an action, we run N simulations, always starting at the root of
# the search tree and traversing the tree according to the UCB formula until we
# reach a leaf node.
def run_mcts(config: MuZeroConfig, root: Node, action_history: ActionHistory,
network: Network):
min_max_stats = MinMaxStats(config.known_bounds)
for _ in range(config.num_simulations):
history = action_history.clone()
node = root
search_path = [node]
while node.expanded():
action, node = select_child(config, node, min_max_stats)
history.add_action(action)
search_path.append(node)
# Inside the search tree we use the dynamics function to obtain the next
# hidden state given an action and the previous hidden state.
parent = search_path[-2]
network_output = network.recurrent_inference(parent.hidden_state,
history.last_action())
expand_node(node, history.to_play(), history.action_space(), network_output)
backpropagate(search_path, network_output.value, history.to_play(),
config.discount, min_max_stats)
由于MuZero不了解环境规则,因此它也不知道在整个学习过程中可能获得的奖励范围到底有多大。MinMaxStats对象用于保存当前遇到的最小奖励和最大奖励的信息,以便MuZero可以相应地将其数值输出标准化。当然,也可以对一个范围已知的游戏直接初始化,如国际象棋 ( − 1 , 1 ) (-1,1) (−1,1) 。
MCTS主循环迭代一共num_simulations次,每次模拟都经过MCTS树抵达一个叶节点(即未探测的节点),然后扩展这个叶节点,再反向计算保存统计信息。现在我们实际走一个模拟循环。
首先,history初始化为从游戏开始至今所采取动作的列表。当前节点node是根节点root,搜索路径search_path仅包含当前节点node。
然后进行模拟,如下图所示:

MuZero首先遍历MCTS树,始终选择UCB(置信上限绑定)分数最高的操作:
# Select the child with the highest UCB score.
def select_child(config: MuZeroConfig, node: Node,
min_max_stats: MinMaxStats):
_, action, child = max(
(ucb_score(config, node, child, min_max_stats), action,
child) for action, child in node.children.items())
return action, child
UCB分数是一个度量标准,使以下两者得到平衡:动作的估计价值 Q ( s , a ) Q(s, a) Q(s,a) ,基于动作选择的先验概率 P ( s , a ) P(s, a) P(s,a)获得的探索奖励,平衡的因素是动作被选的次数 N ( s , a ) N(s, a) N(s,a) 。
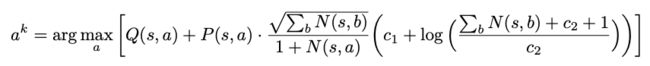
在MCTS树的每个节点上选择UCB分数最高的动作。
模拟初期, N ( s , a ) N(s, a) N(s,a)很小,探索获得的分数占主导地位;但随模拟次数增加,价值 Q ( s , a ) Q(s, a) Q(s,a)变得更加重要(注意: Q ( s , a ) Q(s, a) Q(s,a)在MCTS过程中也一直在调整, P ( s , a ) P(s, a) P(s,a)是不变的)。
最终,进程将抵达一个叶节点(尚未扩展的节点,因此没有子节点)。
在叶节点上,叶节点的父节点调用递归推理recurrent_inference函数,以获得预测的奖励和新的隐藏状态(来自动力学网络)以及新的隐藏状态的策略和价值(来自预测网络)。
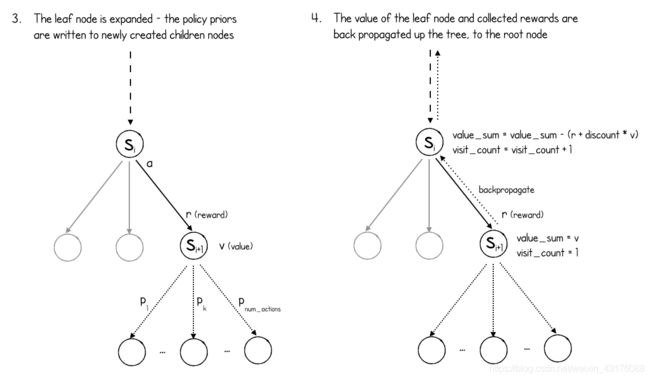
MCTS过程(叶节点扩展和反向传播)
如上图所示,叶节点通过创建新的子节点(游戏中每个可能的动作对应一个子节点)并为每个节点分配相应的策略先验概率。请注意,MuZero不会检查哪些动作是合法的,或者该动作是否导致游戏结束(它不能),因此为每个动作创建一个节点,无论其是否合规。
最后,网络预测的价值沿着搜索路径向上反向传播到整个树。
# At the end of a simulation, we propagate the evaluation all the way up the
# tree to the root.
def backpropagate(search_path: List[Node], value: float, to_play: Player,
discount: float, min_max_stats: MinMaxStats):
for node in search_path:
node.value_sum += value if node.to_play == to_play else -value
node.visit_count += 1
min_max_stats.update(node.value())
value = node.reward + discount * value
注意价值是如何根据轮到谁玩翻转的(叶节点为正是自己,为负是其他玩家)。此外,由于预测网络预测的是未来价值,因此要在搜索路径上收集奖励,计算折扣后添加到叶节点价值中,再被反向传播回树。
记住,这些是预测的奖励,而不是来自环境的实际奖励,收集这些奖励是有意义的,即便对于象棋这样的游戏,真正的奖励只在游戏结束时才被颁发。MuZero正在玩自己想象的游戏,其中甚至包括真实游戏中没有的中间奖励。
这就完成了MCTS过程的一次模拟循环。
经过num_simulations次模拟后,进程停止,并根据根节点下每个子节点被访问的次数选择一个动作。
def select_action(config: MuZeroConfig, num_moves: int, node: Node,
network: Network):
visit_counts = [
(child.visit_count, action) for action, child in node.children.items()
]
t = config.visit_softmax_temperature_fn(
num_moves=num_moves, training_steps=network.training_steps())
_, action = softmax_sample(visit_counts, t)
return action
def visit_softmax_temperature(num_moves, training_steps):
if num_moves < 30:
return 1.0
else:
return 0.0 # Play according to the max.
对于前30个动作,softmax的温度设置为1,这意味着每个动作的选择概率与访问次数成正比。从第30个开始,访问次数最多的动作被选中。

softmax_sample:从根节点选择 α \alpha α 动作的概率(N是访问次数)
尽管以访问次数作为选择最终动作的标准,感觉有点奇怪,但实际上也并不奇怪,因为MCTS过程中的UCB选择标准有意被设计成:一旦在早期对可选方案进行充分探索,就会花更多时间探索可能真正具有高价值的动作。
然后,选定动作被用到真实环境中,相关的值被附加到以下game游戏对象的属性中。
-
game.rewards,在游戏每步中,收到真实奖励的列表 -
game.history,在游戏每步中,采取动作的列表 -
game.child_visits,在游戏每步中,根节点动作概率分布的列表 -
game.root_values,在游戏每步中,根节点价值的列表
这些数据列表非常重要,因为它们最终将用于构建神经网络的训练数据!
这个过程继续进行,游戏每步从头开始创建一个新的MCTS树,并使用它来选择一个动作,直到游戏结束。
所有的游戏数据(rewards,history,child_visits,root_values)被保存到回放缓冲区,然后机器人选手们可以自由地开始一个新游戏。
训练(train_network)
入口函数muzero的最后一行,启动train_network过程,该过程使用回放缓冲区的游戏数据不停地训练神经网络。
def train_network(config: MuZeroConfig, storage: SharedStorage,
replay_buffer: ReplayBuffer):
network = Network()
learning_rate = config.lr_init * config.lr_decay_rate**(
tf.train.get_global_step() / config.lr_decay_steps)
optimizer = tf.train.MomentumOptimizer(learning_rate, config.momentum)
for i in range(config.training_steps):
if i % config.checkpoint_interval == 0:
storage.save_network(i, network)
batch = replay_buffer.sample_batch(config.num_unroll_steps, config.td_steps)
update_weights(optimizer, network, batch, config.weight_decay)
storage.save_network(config.training_steps, network)
它首先创建一个新的Network对象(MuZero三个神经网络的随机初始化实例),并根据已完成的训练步骤数设置学习速率衰减。我们还创建了梯度下降优化器,它将计算每个训练步骤中权重更新的大小和方向。
这个函数的后一部分只是在training_steps(=1,000,000,对于象棋)上循环。每一步,它从回放缓冲区中抽取一个训练批的游戏局势,并用它们来更新网络,每隔checkpoint_interval(=1000)个训练批,会保存一次网络参数。
因此,我们需要讨论两个最后部分——MuZero如何创建一个训练批数据,以及如何使用这些数据来更新三个神经网络的权重。
创建训练批(replay_buffer.sample_batch)
ReplayBuffer类包含一个sample_batch方法,用于从缓冲区中对一批观测结果进行采样:
class ReplayBuffer(object):
def __init__(self, config: MuZeroConfig):
self.window_size = config.window_size
self.batch_size = config.batch_size
self.buffer = []
def sample_batch(self, num_unroll_steps: int, td_steps: int):
games = [self.sample_game() for _ in range(self.batch_size)]
game_pos = [(g, self.sample_position(g)) for g in games]
return [(g.make_image(i), g.history[i:i + num_unroll_steps],
g.make_target(i, num_unroll_steps, td_steps, g.to_play()))
for (g, i) in game_pos]
...
MuZero对国际象棋默认的batch_size是2048。从回放缓冲区中选择出来batch_size盘游戏,并且从每盘游戏中选择一个局势(position)。
单个训练批(batch)的数据结构是一个元组列表,其中每个元组由三个元素组成:
-
g.make_image(i),所选局势的观测值 -
g.history[i : i + num_unroll_steps],所选位置之后的num_unroll_steps个动作的列表 -
g.make_target(i, num_unroll_steps, td_steps, g.to_play),用于训练神经网络的目标列表。具体来说,这是一个元组的列表,元组包括:target_value,target_reward和target_policy。
一训练批(batch)的示例图表如下所示,其中num_unroll_steps = 5 (MuZero使用的默认值):

一个训练批的示例
您可能有点儿疑惑,为什么每个样本都带有一个动作列表?这是因为我们要训练动力学网络,并且唯一的方法就是训练小的序列数据流。
对于一个训练批中的每个样本,我们将利用这些动作从当前位置向未来“展开”num_unroll_steps步。对于初始位置,我们将使用初始推理initial_inference函数来预测价值、奖励和策略,并将其与目标价值、目标奖励和目标策略进行比较。对于后续动作,我们将使用递归推理recurrent_inference函数来预测价值、奖励和策略,并与目标价值、目标奖励和目标策略进行比较。预测值与目标值的差就是损失,训练就是以损失最小化为目标,对三个用于预测的网络的权重同时进行优化。
现在,我们先了解目标,包括目标价值、目标奖励和目标策略,是如何计算出来的。
class Game(object):
"""A single episode of interaction with the environment."""
def __init__(self, action_space_size: int, discount: float):
self.environment = Environment() # Game specific environment.
self.history = []
self.rewards = []
self.child_visits = []
self.root_values = []
self.action_space_size = action_space_size
self.discount = discount
def make_target(self, state_index: int, num_unroll_steps: int, td_steps: int,
to_play: Player):
# The value target is the discounted root value of the search tree N steps
# into the future, plus the discounted sum of all rewards until then.
targets = []
for current_index in range(state_index, state_index + num_unroll_steps + 1):
bootstrap_index = current_index + td_steps
if bootstrap_index < len(self.root_values):
value = self.root_values[bootstrap_index] * self.discount**td_steps
else:
value = 0
for i, reward in enumerate(self.rewards[current_index:bootstrap_index]):
value += reward * self.discount**i # pytype: disable=unsupported-operands
if current_index < len(self.root_values):
targets.append((value, self.rewards[current_index],
self.child_visits[current_index]))
else:
# States past the end of games are treated as absorbing states.
targets.append((0, 0, []))
return targets
...
make_target函数使用时差学习(TD-learning)的思想,计算从state_index到state_index + num_unroll_steps棋局中每个状态的目标价值。变量为current_index。
时差学习(TD-learning)是强化学习中常用的一种技术,其思想是,为了更新某一状态的价值,我们用当前状态到未来td_steps步棋局之前拿到的实际奖励的贴现值,加上td_steps步棋局的估计价值的贴现值,来更新当前状态的价值;而不是用整盘游戏结束时累积的奖励贴现值。
这种用一个估计值去更新另一个估计值得方法,我们称之为自举(bootstrapping)。bootstrap_index是未来td_steps步棋局的索引,我们将用它索引的价值,估计未来真实奖励。
make_target函数首先检查bootstrap_index是否超出这盘游戏。如果是,value为0,否则value为bootstrap_index棋局预测价值的贴现值;然后,再加上current_index和bootstrap_index之间发生的真实奖励的贴现值。
最后,检查current_index是否超出这盘游戏。如果超出,则添加空的目标值;否则,将从MCTS计算出的TD目标价值、真实奖励和策略(根节点下子节点的访问计数)将添加到目标列表中。
对于国际象棋来说,td_steps实际上设置为max_moves,这样bootstrap_index总会持续到一盘游戏有结局。在这种情况下,我们实际上使用的是蒙特卡罗估计的目标值(即直到游戏结束时所有未来奖励总和贴现值)。这是因为国际象棋的奖励只在一盘游戏结束时颁发。时差学习(TD-learning)与蒙特卡罗估计的区别如下图所示:

TD-learning与蒙特卡罗法在目标值设定上的不同
我们已经了解了目标值以及训练数据批是如何构建的,现在我们可以了解它们是如何用于MuZero的loss函数的,最后,我们可以了解它们是如何在update_weights函数中用于训练网络的。
MuZero 损失函数
Muzero的损失函数如下:

这里,K是num_unroll_steps的变量。换言之,我们努力将三个损失降到最低:
t时刻,k步的预测奖励(r)与实际奖励(u)之间的差值t时刻,k步的预测价值(v)与TD目标价值(z)之间的差值t时刻,k步的预测策略(p)与MCTS策略(pi)之间的差异
这些损失在展开的num_unroll_steps期间相加,以生成一批中给定位置的损失;其中,还有一个正规化的项用来对付网络中的大权重。
更新三个MuZero网络(update_weights)
def update_weights(optimizer: tf.train.Optimizer, network: Network, batch,
weight_decay: float):
loss = 0
for image, actions, targets in batch:
# Initial step, from the real observation.
value, reward, policy_logits, hidden_state = network.initial_inference(image)
predictions = [(1.0, value, reward, policy_logits)]
# Recurrent steps, from action and previous hidden state.
for action in actions:
value, reward, policy_logits, hidden_state = network.recurrent_inference(hidden_state, action)
predictions.append((1.0 / len(actions), value, reward, policy_logits))
hidden_state = tf.scale_gradient(hidden_state, 0.5)
for prediction, target in zip(predictions, targets):
gradient_scale, value, reward, policy_logits = prediction
target_value, target_reward, target_policy = target
l = (
scalar_loss(value, target_value) +
scalar_loss(reward, target_reward) +
tf.nn.softmax_cross_entropy_with_logits(
logits=policy_logits, labels=target_policy))
loss += tf.scale_gradient(l, gradient_scale)
for weights in network.get_weights():
loss += weight_decay * tf.nn.l2_loss(weights)
optimizer.minimize(loss)
update_weights函数为每一批中的2048个棋局逐一构建损失。
首先让初始观测通过初始推理initial_inference网络,预测当前位置value,reward和policy。这些用于创建predictions列表,以及给定权重1.0。
然后,每个动作依次循环,并要求递归推理recurrent_inference函数根据当前hidden_state状态和动作预测下一个value,reward和policy。这些被附加到predictions列表中,权重为1/num_rollout_steps(这样循环recurrent_inference函数的总权重等于initial_inference函数的权重)。
然后,我们计算predictions与其相应的目标值比较的损失,这是奖励和价值的标量损失、以及policy的softmax_crossentropy_loss_with_logits的组合。
然后,优化此损失函数就等于同时训练所有三个MuZero网络。
所以呢。。。这就是你用Python训练MuZero的方法。
总结
总之,AlphaZero天生就知道三件事:
-
采取某一特定动作时棋盘上会发生什么。例如,如果它执行“将卒子从e2移到e4”的动作,它知道下一个棋局是相同的,只是卒子已经移动了。
-
在一个特定的位置上,合规的动作是什么。例如,AlphaZero知道如果你的皇后不在棋盘上,一个棋子挡住了移动,或者你已经在c3上有了一个棋子,你就不能移动“皇后到c3”。
-
当比赛结束,谁赢了。例如,它知道如果对手的国王处于控制之中,并且不能脱离控制,它就赢了。
换句话说,AlphaZero可以想象未来,因为它知道游戏规则。
在整个训练过程中,MuZero不使用这些基本的游戏机制。值得注意的是,通过添加两个额外的神经网络,它能够应付不知道规则的情况。
事实上,MuZero更具生命力。
难以置信的是,MuZero在围棋中的实际表现超越了AlphaZero。这可能暗示,与AlphaZero使用真实棋局的方法相比,MuZero正在寻找更有效的方法通过其隐藏表征来表示棋局。MuZero将游戏嵌入自己大脑的神秘方式肯定会成为DeepMind近期的一个活跃研究领域。

MuZero在国际象棋、日本将棋、围棋和Atari游戏中的表现总结。
最后,我想简单总结一下为什么我认为这个发展对人工智能非常重要。
为什么这是件大事儿
AlphaZero已经被认为是迄今为止人工智能最伟大的成就之一,它在一系列游戏中实现了超人的能力,不需要人类的专业知识作为输入。
表面上看,这似乎有点奇怪,以这么多额外努力就是为了证明这个算法不了解规则也无妨吗?这有点像成为国际象棋世界冠军之后,闭上眼睛打未来所有的比赛。难道这只是派对上的装逼把戏吗?
答案是,对DeepMind而言,从来不是真的就事论事于围棋、国际象棋或任何其他游戏。这关系到智能的本质。
你学游泳的时候,并没有先拿到流体力学的规则手册。你学会搭积木造高塔时,却还没掌握牛顿的万有引力定律。你学会说话时,根本不懂任何语法,可能直到今天,你仍然很难向非母语者解释语言的所有规则和怪癖。
关键是,生命没有规则也可以学习!
这项工作仍然是宇宙中的大秘密。这就是为什么它是如此重要,我们正在探索的方法——强化学习,不需要知道环境的作用机制仍然可以提前规划。
MuZero论文与同样令人印象深刻的WorldModels论文(Ha, Schmidhuber)有异曲同工之妙。两者都创建了智能体内部使用的环境表征,并用于想象可能的未来,以便训练模型实现目标。两篇论文实现目标的方式不同,但却有一些相似之处:
- MuZero使用表征网络嵌入当前观测,WorldModels使用变分自动编码器。
- MuZero使用动力学网络对想象的环境进行建模,WorldModel使用递归神经网络。
- MuZero使用MCTS和预测网络来选择动作,World Models使用进化过程来进化最优动作控制器。
这是一个好兆头,两个想法兼具开创性和各自的特点,却实现了同样的目标。这很可能意味着双方都发现了一些更深层次的真相——也许这两把铁锹恰好击中了藏宝箱的不同部位。
这是“如何使用Python构建自己的MuZero AI”系列文章的结尾,希望你喜欢。
