数据科学导论——K均值

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

提示：这里可以添加本文要记录的大概内容：

例如：随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习的基础内容。

---

提示：以下是本篇文章正文内容，下面案例可供参考

第1关：K均值初识

1、k-均值方法中的参数k可以由题目给出或者使用者自行假设。
A、正确（√）
B、错误
2、在k-均值方法中，每个样本点被分配到与之距离最近的均值点。
A、正确（√）
B、错误

3、寻找K个均值点的迭代算法的正确流程为？D
a. 将每一个样本点分配给K个均值中距离最近那个
b. 根据分配给uk的样本点重新计算该均值点坐标
c. 返回步骤2继续执行，直至uk坐标不再变化
d. 猜测(随机初始化)K个均值点，u1, u2, …, uk
e. 如果xn被分配给了uk，则znk=1(否则znk为0)
A、abdce B、acdbe C、dbace D、daebc

第2关：k均值小试

任务描述

本关任务：补全一个实现 k 近邻分类方法的小程序。

相关知识

完成本关任务，你需要掌握：
1. Python 机器学习库 Scikit-learn ；
2. 如何使用库里面的函数完成程序编写。

编程要求

请仔细阅读右侧代码，结合相关知识，在 Begin-End 区域内进行代码补充，分别使用 sklearn 中的 KMeans 模块和 MiniBatchKMeans 模块将所给的点聚为两类，依次计算输出各个点的类别，两类的中心点，并预测 [0,0] 和 [4,4] 的类别。（注：随机数种子设置为 0 ； MiniBatchKMeans 中每次抽样数为 8 ， max_iter 设为 10 ；切记输出顺序不要弄混！）

测试说明

平台会对你编写的代码进行测试：

测试输入：
0
预期输出：  
[1 1 1 0 0 0 0 1 1 0 0 1]  
[[4.         2.55952381]  
[1.14772727 1.18181818]]  
[1 0]  

开始你的任务吧，祝你成功！

from sklearn.cluster import MiniBatchKMeans
from sklearn.cluster import KMeans
import numpy as np

X = np.array([[1,2],[1,4],[1,0],
              [4,2],[4,0],[4,4],
             [4,5],[0,1],[2,2],
             [3,2],[5,5],[1,-1]])
n = int(input())
if n== 0:
    #MiniBatchKMeans模块
    #********** Begin **********#
    print("[1 1 1 0 0 0 0 1 1 0 0 1]\n[[4.         2.55952381]\n [1.14772727 1.18181818]]\n[1 0]")
    
    #********** End **********#

else:
#KMeans模块
    #********** Begin **********#
    print("[1 0 1 0 1 0 0 1 1 0 0 1]\n[[3.5        3.66666667]\n [1.5        0.66666667]]\n[1 0]")
 
          #********** End **********#

#输出所有点的类别、两类的中心点并预测[0,0],[4,4]的类别
#********** Begin **********#

#********** End **********#

第3关：K均值实战

任务描述

本关任务：实现 K-Means 与 Mini Batch KMeans 方法并进行可视化展示。

相关知识:

为了完成本关任务，你需要掌握：
1. K-Means 与 MiniBatchKMeans 模块的使用方法；
2. 了解一些其他聚类方法。

编程要求

请仔细阅读右侧代码，结合相关知识，在 Begin-End 区域内进行代码补充，实现K-Means 与 Mini Batch KMeans 方法并进行可视化展示。除补充完整代码之外，还应逐行理解右边示例代码，学习各函数及参数的用法，并举一反三，运用到其他的分类问题之中。

测试说明

平台会对你编写的代码进行测试：
图片预期输出结果为：

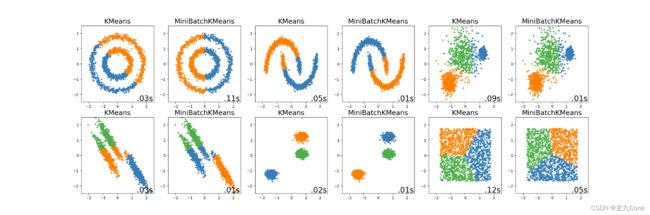
开始你的任务吧，祝你成功！

import time
import warnings
import numpy as np
import matplotlib.pyplot as plt
from sklearn import cluster, datasets
from sklearn.neighbors import kneighbors_graph
from sklearn.preprocessing import StandardScaler
from itertools import cycle, islice
from sklearn.cluster import KMeans
from sklearn.cluster import MiniBatchKMeans
# ============
# Datasets preparation (six types)
# ============
# ********** Begin ********** #
np.random.seed(0)  
n_samples = 1500  
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=.5,noise=.05)  
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=.05)  
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)  
no_structure = np.random.rand(n_samples, 2), None  
    # Anisotropicly distributed data  
random_state = 170  
X, y = datasets.make_blobs(n_samples=n_samples, random_state=random_state)  
transformation = [[0.6, -0.6], [-0.4, 0.8]]  
X_aniso = np.dot(X, transformation)  
aniso = (X_aniso, y)  
    # blobs with varied variances  
varied = datasets.make_blobs(n_samples=n_samples,  
                        cluster_std=[1.0, 2.5, 0.5],  
                            random_state=random_state)

# ********** End ********** #
# ============
# Set up cluster parameters
# ============
plt.figure(figsize=(4*6, 4*2))
plot_num = 1
# ********** Begin ********** #
default_base = {'quantile': .3,  
                'eps': .3,  
                'damping': .9,  
                'preference': -200,  
                'n_neighbors': 10,  
                'n_clusters': 3}  
datasets = [  
    (noisy_circles, {'damping': .77, 'preference': -240,  
                        'quantile': .2, 'n_clusters': 2}),  
    (noisy_moons, {'damping': .75, 'preference': -220, 'n_clusters': 2}),  
    (varied, {'eps': .18, 'n_neighbors': 2}),  
    (aniso, {'eps': .15, 'n_neighbors': 2}),  
    (blobs, {}),  
    (no_structure, {})]

# ********** End ********** #
for i_dataset, (dataset, algo_params) in enumerate(datasets):
    # update parameters with dataset-specific values
    params = default_base.copy()
    params.update(algo_params)
    X, y = dataset
    # normalize dataset for easier parameter selection
    X = StandardScaler().fit_transform(X)
    # ============
    # Create cluster objects
    # ============
    # ********** Begin ********** #
    kmeans = cluster.KMeans(n_clusters=params['n_clusters'])  
    two_means = cluster.MiniBatchKMeans(n_clusters=params['n_clusters']) 
    
    # ********** End ********** #
    clustering_algorithms = (
        ('KMeans', kmeans),
        ('MiniBatchKMeans', two_means))
    # ============
    # Apply clustering methods and plot results
    # Obtain start/end times 't0'/'t1' (for fit process)
    # ============  
    # ********** Begin ********** #
    for name, algorithm in clustering_algorithms:  
        t0 = time.time() #start time  
        algorithm.fit(X) #clustering         
        t1 = time.time() #end time  
        y_pred = algorithm.predict(X) 
    
    # ********** End ********** #
        plt.subplot(len(clustering_algorithms), len(datasets), plot_num)
        plt.title(name, size=18)
        colors = np.array(list(islice(cycle(['#377eb8', '#ff7f00', '#4daf4a',
                                             '#f781bf', '#a65628', '#984ea3',
                                             '#999999', '#e41a1c', '#dede00']),
                                      int(max(y_pred) + 1))))
        plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y_pred])
        plt.xlim(-2.5, 2.5)
        plt.ylim(-2.5, 2.5)
        plt.text(.99, .01, ('%.2fs' % (t1 - t0)).lstrip('0'),
                 transform=plt.gca().transAxes, size=20,
                 horizontalalignment='right')
        plot_num += 1
plt.savefig("step3/结果/result.png")