联邦学习原始论文解读

前言

  联邦学习(Federated Learning) 是人工智能的一个新的分支，这项技术是谷歌于2016年首次提出，本篇论文第一次描述了这一概念。

Abstract

  现代移动设备可以访问到大量数据，这些数据训练后反过来可以大大提高用户体验。例如，语言模型可以改善语音识别和文本输入，图像模型可以自动选择好的照片。但是，这些丰富的数据通常对隐私敏感、数量众多或两者兼而有之，这可能会妨碍使用常规方法进行训练。于是我们提出将训练数据分发在移动设备上的替代训练方案，并通过聚合本地计算的更新来学习共享模型，我们称这种分散的学习方法为联邦学习。

  简而言之，当下移动设备产生了大量的数据，我们需要利用这些数据来训练一些模型，这些模型将会提升用户实验。传统的训练方式：收集所有客户端的数据，然后利用这些数据训练一个模型，最后分发给所有客户端。存在的问题：我们没法直接收集所有设备的数据来统一训练（隐私要求），于是提出了一种新的不需要共享客户端数据的模型训练方式。

Introduction

  联邦学习中，学习任务由中央服务器协调，每个客户端都有一个本地训练数据集，该数据集永远不会上传到服务器（即隐私不会被泄露）。

  本文主要贡献：

• 将移动设备分散数据的训练问题确定为重要的研究方向
• 提出了解决该问题的具体算法
• 对所提出的算法进行了验证

  更具体地说，我们引入了联邦平均算法(FederatedAveraging algorithm)。

Federated Learning

  联邦学习的问题具有以下属性：

• 对来自移动设备的数据进行训练，与对数据中心通常可用的代理数据进行训练相比，具有明显的优势。
• 该数据是隐私敏感的或者大规模的（与模型的大小相比），因此最好不要纯粹出于模型训练的目的将其记录到数据中心（隐私的）
• 对于监督任务，可以从用户交互中自然推断出数据上的标签。

  作为两个例子，我们考虑图像分类和语言模型。图像分类：例如预测哪些照片将来最有可能被多次查看或共享；语言模型：下一个单词的预测甚至预测整个回复来改善触摸屏键盘上的语音识别和文本输入。这两项任务的潜在训练数据（用户拍摄的所有照片以及他们在移动键盘上键入的所有照片，包括密码，URL，消息等）都可能对隐私敏感。

Privacy

  与数据中心对持久数据的训练相比，联邦学习具有明显的隐私优势。但是即使是“匿名”数据集，也可能通过与其他数据结合而使用户隐私面临风险。

Federated Optimization

  我们将联邦学习中的优化问题称为联邦优化（Federated Optimization）。联邦优化具有几个关键属性，可将其与典型的分布式优化问题区分开：

• Non-IID：给定客户端上的训练数据通常基于特定用户对移动设备的使用，因此任何特定用户的本地数据集将不代表总体分布。
• Unbalanced：一些用户将比其他用户更重地使用服务或应用程序，导致不同数量的本地培训数据。简而言之，每个用户产生的数据量不一样。
• Massively distributed：预计参与优化的客户端数量将远远大于每个客户端的平均示例数量。
• 移动设备经常脱机或连接缓慢或昂贵。

  本文重点是非IID和不平衡属性的优化，以及通信约束的关键性质。

  我们假设一个同步更新方案在几轮通讯中进行。有一组固定的K个客户端，每个客户端都有一个固定的本地数据集。在每轮开始时，随机选择一部分客户端，服务器将当前全局算法状态发送给这些客户端中的每一个（例如，当前模型参数）。然后，每个选定的客户端根据全局状态及其本地数据集执行本地计算，并向服务器发送更新。然后，服务器将这些更新应用于其全局状态，并重复该过程。

  问题的一般形式：

  公式1：$f_i(w)=l(x_i,y_i;w)$表示第i个样本的损失，即最小化所有样本的平均损失。

  公式2：$F_k(w)$表示一个客户端内所有数据的平均损失，$f(w)$表示当前参数下所有客户端的加权平均损失。

  值得注意的是，如果所有$P_k$（第k个客户端的数据）都是通过随机均匀地将训练样本分布在客户端上来形成的，那么每一个$F_k(w)$的期望都为$f(w)$。这是通常由分布式优化算法做出的IID假设：即每一个客户端的数据相互之间都是独立同分布的。

  在数据中心优化中，通信成本相对较小，计算成本占主导地位，最近的重点是使用GPU来降低这些成本。相比之下，在联邦优化通信成本中占主导地位。

  因此，我们的目标是使用额外的计算来减少训练模型所需的通信轮数。我们可以添加计算的两种主要方法：

• 增加并行性。使用更多客户端在每个通信周期之间独立工作。
• 增加对每个客户端的计算。即每个客户端在每个通信回合之间执行更复杂的计算。

  以上内容下文都将有更加详细的介绍！

The FederatedAveraging Algorithm

  深度学习的众多成功应用几乎完全依赖于随机梯度下降（SGD）的变体进行优化。

  在联邦学习中，我们使用大批量同步SGD，已有相关论文证明，它是优于异步方法的。

  为了在联邦学习中应用这种方法，我们在每轮中选择一部分客户端，并计算这些客户端持有的所有数据的损失梯度。参数C控制全局块大小，其中C=1对应于全批（非随机）梯度下降。我们将此算法称为FederatedSGD（orFedSGD）。

  FedSGD的一种典型的实现方式：C=1（非SGD），学习率$\eta$固定，每一个客户端算出自己所有数据损失的梯度（平均梯度），然后传递给中央服务器，中央服务器整合所有梯度，来更新全局的参数$w_t$。

  计算量由三个参数控制：

• C：每一轮执行计算的客户端比例（只有一部分客户端参与更新）
• E：每一轮更新时，每个客户端对其本地参数进行更新的次数
• B：客户端每一次更新参数时所用本地数据量的大小

   该算法更加详细的描述如下：

  参数介绍：$K$表示客户端的个数，$B$表示每一次本地更新时的数据量，$E$表示本地更新的次数，$\eta$表示学习率。

  首先是服务器执行以下步骤：

1. 初始化参数
2. 对第t轮训练来说：首先计算出$m=max(C\cdot K,1)$，然后随机选择m个客户端，对这m个客户端做如下操作（所有客户端并行执行）：更新本地的$w_t^k$得到$w_{t+1}^k$。所有客户端更新结束后，将$w_{t+1}^k$传到服务器，服务器整合所有$w_{t+1}^k$得到最新的全局参数$w_{t+1}$。
3. 服务器将最新的$w_{t+1}$分发给所有客户端，进行下一轮的更新。

   对每一个本地客户端来说，要做的就是更新本地参数，具体来讲：

1. 把自己的数据集按照参数B分成若干个块，每一块大小都为B。
2. 对每一块数据，需要进行E轮更新：算出该块数据损失的梯度，然后进行梯度下降更新，得到新的本地$w$
3. 更新完后$w$将被传送到中央服务器，服务器整合所有客户端计算出的$w$，得到最新的全局模型参数$w_{t+1}$
4. 客户端收到服务器发送的最新全局参数模型参数，进行下一次更新。

Experimental Results

   Table1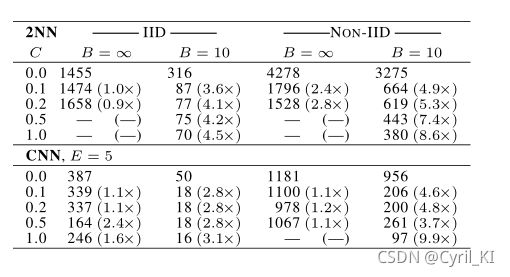：   表1描述的是图像分类任务：参数C对E=1的MNIST 2NN和E=5的CNN的影响。其中C=0表示每次选择一个客户端的数据进行更新。对于MINST 2NN来说，总的客户端数量为100，即五行分别表示1,10,20,50,100个客户端。

  每个表格条目给出了实现2NN的97%和CNN的99%的测试集精度所需的通信轮数，以及相对于C=0这一baseline的加速比。 比如对于第三行$B=\infty$这一情况（$B=\infty$表示每一次都用全部数据进行本地参数更新），中央服务器需要与客户端进行1658次通信，才能使得模型在测试集上的精度达到97%。

  Table2：

  表2描述的是语言模型：LSTM语言模型，该模型在读取一行中的每个字符后预测下一个字符。该模型以一系列字符作为输入，并将每个字符嵌入到8维空间中，然后通过2个LSTM层处理嵌入的字符，每个层具有256个节点。

  表2的含义同表1：在某一参数环境下，FedSGD要达到目标精度所需要进行的通讯次数。

  SGD对学习率参数η的调整很敏感，本文的$\eta$是基于网格搜索法找到的。

Increasing parallelism

  增加并行性： 即增加客户端数量。

  上图给出了特定参数设置下要达到阈值精度（图中灰线）所需要进行的通讯轮数。

  然后，使用形成曲线的离散点之间的线性插值来计算曲线穿过目标精度的轮数。

Increasing computation per client

  增加每个客户端的计算量。C=0.1固定，减小B，或者增加E，或者减小B的同时增加E。

  还是上面这张图：

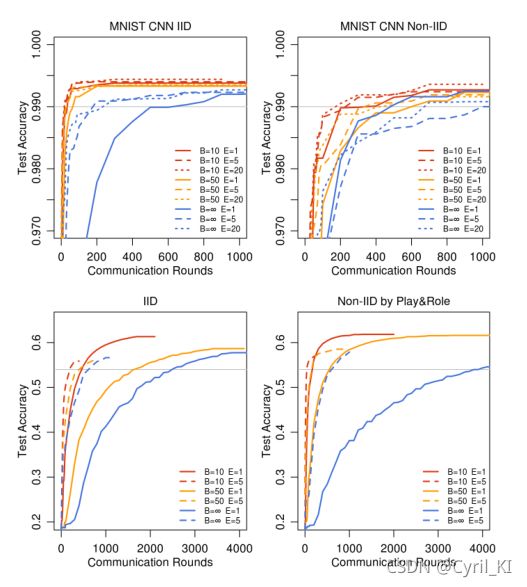
  可以看到，随着B减小或者E增加，达到目标精度所需的通讯次数是减小的，也就是说：每轮添加更多本地SGD更新可以显著降低通信成本。

Can we over-optimize on the client datasets?

  本地数据集上进行更新时可以过度优化吗？即E特别大，进行很多次的本地更新。

  上图给出了E特别大时的实验结果：对于大的E值，收敛速度并没有显著的下降。

Conclusions and Future Work

  联邦学习可以变得切实可行，因为可以使用相对较少的通信轮次来训练高质量模型。联邦学习将是未来比较热门的一个方向！

  欢迎大家关注我的微信公众号：KI的算法杂记，有什么问题可以添加微信或者直接发私信询问。