局部加权线性回归

前言：

在数据处理或图像处理中，回归往往可以达到很好的效果。

回归的目的就是训练算法，进而找到回归系数。

1、线性回归

怎样从一大堆数据里求出回归方程呢？

假定输入数据存放在矩阵X中，回归系数存放在向量w中，那么对于给定的数据X₁，预测结果Y₁ = X₁^Tw。

问题点：有一些X和对应的Y，怎么找到w?

常用的方法是找到一个w，使得误差最小。这里的误差指的是预测值y与真实值y之间的差值。

平方误差写作：${\sum }_{i=1}^m$(y_i - x_i^Tw)²

用矩阵表示可以写作(y - xw)^T(y - xw)。对w求导，得到x^T(y - xw),令其等于0，解出w如下：

其中w^~ 是当前可以估计出的w最优解（而非真实w值）

尝试对以下散点图找出最佳拟合直线

程序清单1：标准回归函数

def standRegress(xArr , yArr):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    xTx = xMat.T*xMat
    if 0.0 == np.linalg.det(xTx) :
        print("This matrix is singular, cannot do inverse . ")
        return
    ws = xTx.I * (xMat.T * yMat)
    return ws

绘制出的拟合直线如下

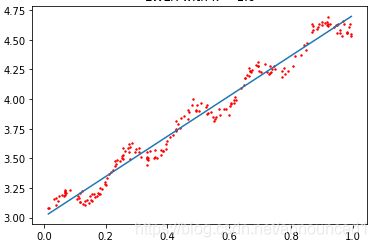
最佳拟合直线方法表现不错，但欠拟合也挺严重的。

2、局部加权线性回归

模型欠拟合将不能取得最好的预测效果。所以有些方法允许在估计中引入一些偏差，从而降低预测的均方误差。

其中一个方法—局部加权线性回归。该方法中，给待测点附近的每个点赋予一定权重。

其中W是一个矩阵，用来给每个数据点赋予权重。

LWLR使用"核"来对附近的点赋予更高的权重。本例使用高斯核，高斯核对应的权重如下:

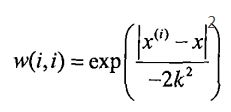
这样就构建了一个只含对角元素的权重矩阵W(该W即为上式的权重矩阵)，其中x表示待预测点，x⁽ⁱ⁾表示待预测点附近的点。
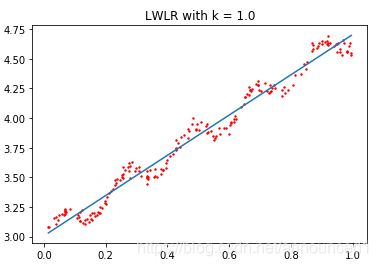
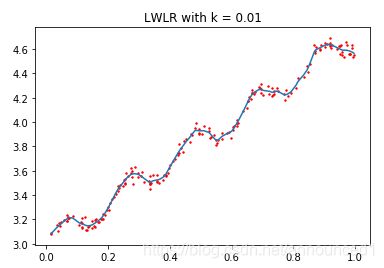
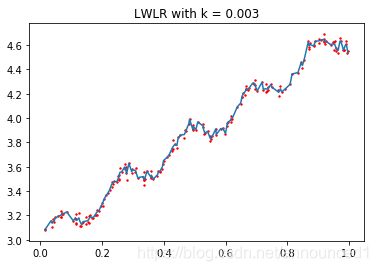
x与x⁽ⁱ⁾越近,w(i,i)越大。k是一个需要用户指定的参数，k决定了对附近点赋予多大的权重。
下图绘制了k与权重的关系

程序2：局部加权线性回归函数

#########################
##函数描述：计算权重
##testPlint ：某个待测点
## xArr  ， yArr ：数据点 
#########################
def lwlr(testPlint , xArr , yArr , k = 1.0 ):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    m = np.shape(xMat)[0]
    weights = np.mat(np.eye((m)))  #创建对角矩阵，为每个样本点初始化一个权重
    for j in range(m):  #计算每个样本点对应的权重值
        diffMat = testPoint - xMat[ j , : ]
        #随着样本点与待测点距离的递增，权重将以指数级衰减，参数k控制衰减速度
        weights[j , j ] = np.exp((diffMat * diffMat.T)/(-2*k**2))   
    xTx = xMat.T * ( weights * xMat )
    if (0.0 == np.linalg.det(xTx)):
        print("This matrix is singular, cannot do inverse . ")
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoints * ws


#########################
##函数描述：计算预测结果
##testArr ：待测矩阵
## xArr  ， yArr ：数据点 
#########################
def lwlrtest(testArr , xArr , yArr , k = 1.0):
    m = np.shape(testArr)[0]   #样本数目
    yHat = zeros(m)
    for j in range(m):
        yHat[i] = lwlr(testArr[i] , xArr , yArr , k )
    return yHat

拟合结果如下图:
欠拟合

拟合

过拟合