优化器、学习率理论，代码

1、牛顿迭代法

公式：

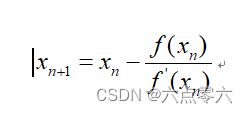
牛顿迭代法是最早出现的用于求函数零点的迭代算法，随机给定一个函数和一个初值（x1，y1），就可以逐步迭代得到一个x，使得f（x）=0。

现在在二维平面上来求一下f（x）=x^2的零点，首先这个函数的导数为 2*x，给初值（6，36）。

上面给出前两步的推导，后面的可以自己算，在第十步的时候x（10）=0.0059。

给牛顿公式加上一个学习率η，变成这个样子：

如果加入的学习率小于一的话，那上一步的x所要减去的值就相对变少一点，如果学习率大于一的话，那上一步的x所要减去的值就相对变多一点，如果学习率小于零的话，那迭代出来的x值就会远离最近的零点。

放在三维或者更高维的情况下，将导数成为梯度，梯度是一个向量，其中的元素为函数对各个自变量的偏导数，向量为一个有方向的矢量，沿着梯度方向自变量的值会变大，沿着梯度负方向才会找到最近的极小值点。

上面就是优化器的基本原理，当然除了牛顿迭代法还有其他的好多方法，大差不差。

2、代码实现

先搭建一个简易网络并且实例化

import torch.optim as optim
import torch
import torch.nn as nn


epoch = 3

data = torch.randn((4,3,5,5))
label = torch.tensor([0,0,1,1])
class Net(nn.Module):
    def __init__(self,in_channels,out_channel,cls):
        super(Net, self).__init__()
        self.conv = nn.Conv2d(in_channels,out_channel,kernel_size=(3,3))
        self.bn = nn.BatchNorm2d(out_channel)
        self.Relu = nn.ReLU()
        self.avg = nn.AdaptiveAvgPool2d((1,1))
        self.Linear = nn.Linear(out_channel,cls)
    def forward(self,x):
        x = self.conv(x)
        x = self.bn(x)
        x = self.Relu(x)
        x = self.avg(x)
        x = torch.flatten(x,1)
        x = self.Linear(x)
        return x

net = Net(3,4,3)
loss_fun = nn.CrossEntropyLoss()

加入优化器，优化器的种类有很多，这里以Adam为例，

params = [param for param in net.parameters()]
optimizer = optim.Adam(params,lr=0.01)

可以打印optimizer中的信息

print(optimizer)

打印结果

Adam (
Parameter Group 0
    amsgrad: False
    betas: (0.9, 0.999)
    eps: 1e-08
    lr: 0.01
    weight_decay: 0
)

先介绍打印信息中的 “lr” 的两种调整方法

1、在官网中介绍了十四种学习率的调整方式，以其中一种为例，当epoch>4的时候就会调整学习率为lr = 0.01/0.5,小于4的时候就是0.01
torch.optimi

#  在优化器下面加入这一行代码
scheduler1 = optim.lr_scheduler.ConstantLR(optimizer , factor=0.5, total_iters=4)

# 这是训练循环，包括向后传播，更新梯度（导数），梯度清零，更新学习率，最后四行代码必须写
for epoch in range(epoch):
    pred = net(data)
    loss_run = loss_fun(pred,label)
    loss_run.backward()
    optimizer.step()
    optimizer.zero_grad()
    scheduler1.step()

2、学习率和参数存储在optimizer.param_groups，可以调用这个api将lr提取出来并进行赋值

先定义学习率调整方式，这个自己可以设置

def lr_scheduler(lr,factor,epoch):
    if epoch >= 4:
        lr = lr/factor
    else:
        lr = lr
    return lr

动态调整学习率

for epoch in range(epoch):
    for param_grop in optimizer.param_groups:
        lr = param_grop["lr"]
        # 完成更新
        param_grop["lr"] = lr_scheduler(lr,0.5,epoch )
    pred = net(data)
    loss_run = loss_fun(pred,label)
    loss_run.backward()
    optimizer.step()
    optimizer.zero_grad()

用上面定义的那个优化器是直接传入的权重参数和学习率，也可以用另一种方式传入权重参数和学习率，如下，pg1和pg2都为列表，其中分别装着卷积层和全连接层的参数（或者也可以自己设置，根据层结构名称将权重装进一个列表，并设置学习率），这样子就可以实现不同网络结构有不同的学习率

如何拿到网络模型的参数，可以参考：
查看权重

optimizer.add_param_group({"params": pg1,"lr":lr})
optimizer.add_param_group({"params": pg2,"lr",lr})

在优化器这块还有权重衰减、动量的知识以后补充