【Simulink模块】低通/高通滤波器模块介绍及其Simulink仿真教程

 

simulink自带模块   Analog Filter Design

描述：

模拟滤波器设计模块以高通，低通，带通或带阻配置设计和实现Butterworth，I型Chebyshev，II型Chebyshev，椭圆或贝塞尔滤波器。

输入必须是基于样本的连续时间实值标量信号。

可以从对话框的“设计方法”和“滤波器类型”弹出菜单中选择滤波器的设计和频带配置。 对于设计方法和频段配置的每种组合，都会显示一组适当的辅助参数。

 

滤波器的种类

 

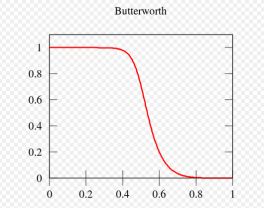
Butterworth 

巴特沃斯滤波器：巴特沃思滤波器的幅度响应在通带和单调总体上最大平坦。

图示：

特性：

巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦，没有起伏，而在阻频带则逐渐下降为零。 在振幅的对数对角频率的波特图上，从某一边界角频率开始，振幅随着角频率的增加而逐步减少,趋向负无穷大。

传递函数：

存在缺陷：

巴特沃斯滤波器是滤波器的—种设计分类，类同于切比雪夫滤波器，它有高通，低通，带通，高通，带阻等多种滤波器。它在通频带内外都有平稳的幅频特性，但有较长的过渡带，在过渡带上很容易造成失真，在调用 MATLAB里的巴特沃斯滤波器做仿真时，信号总会在第一个周期略微有些失真。但往后的幅频特性就非常的好

Chebyshev type I

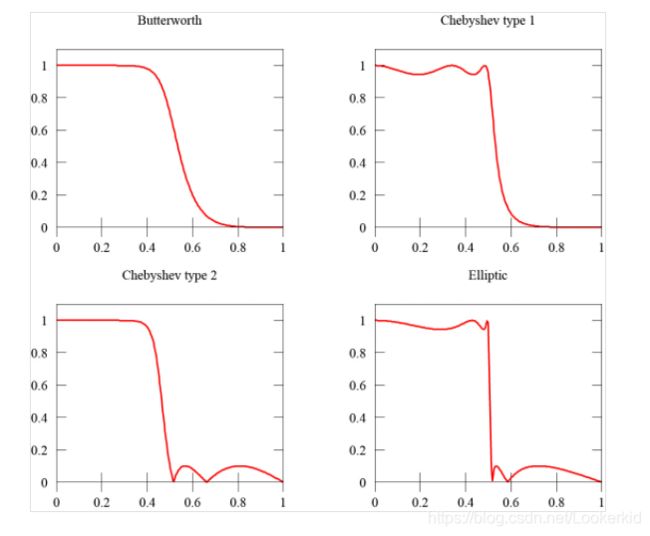
切比雪夫Ⅰ型：Chebyshev I型滤波器的幅度响应在通带中是等波纹的，在阻带中是单调的。

Chebyshev type II

切比雪夫ⅠI型：Chebyshev II型滤波器的幅度响应在通带中是单调的，在阻带中是等波纹的。

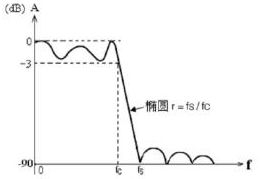
Elliptic

椭圆滤波器：椭圆滤波器的幅度响应在通带和阻带中都是等波纹的。

图示：

特性：

传递函数来看，巴特沃斯和切比雪夫滤波器的传递函数是一个常数除以一个多项式, 为全极点网络,仅在无限大阻带处衰减为无限大而椭圆函数滤波器在有限频率上既有零点又有极点。极零点在通带内产生等波纹。阻带内的有限传输零点减少了过渡区，可获得极为陡峭的衰减曲线。也就昰说在阶数相同的条件下，椭圆滤波器相比于其他类型的滤波器，能茯得更窄的过渡带宽和较小的阻带波动，就这点而言，椭圆滤波器是最优的。它陡峭的过渡带特性是用通带和阻带的起伏为代价来换取的。

 

Bessel

贝塞尔滤波器：贝塞尔滤波器的幅度响应在通带中最大平坦，总体上是单调的。 该滤波器具有最大平坦的线性相位响应。

图示：

特性：

贝塞尔(Bessel)滤波器具有最平坦的幅度和相位响应。带通（通常为用户关注区域）的相位响应近乎呈线性。Bessel滤波器可用于减少所有IIR滤波器固有的非线性相位失真。

虽然贝塞尔滤波器在它的通频带内提供平坦的幅度和线性相位（即一致的群延时）响应，但它的选择性比同阶（或极数）的巴特沃斯(Butterworth)滤波器或切比雪夫(Chebyshev)滤波器要差。因此，为了达到特定的阻带衰减水平，需要设计更高阶的贝塞尔滤波器，从而它又需要仔细选择放大器和元件来达到最低的噪声和失真度。

传递函数：

几种滤波器对比

 

下表列出了每种设计/频段组合的可用参数。 对于低通和高通频带配置，这些参数包括通带边沿频率Ωp，阻带边沿频率Ωs，通带纹波Rp和阻带衰减Rs。 对于带通和带阻配置，参数包括上下通带边缘频率Ωp1和Ωp2，下限和上阻带边缘频率Ωs1和Ωs2，通带纹波Rp和阻带衰减Rs。 频率值以rad / s为单位，纹波和衰减值以dB为单位。

 

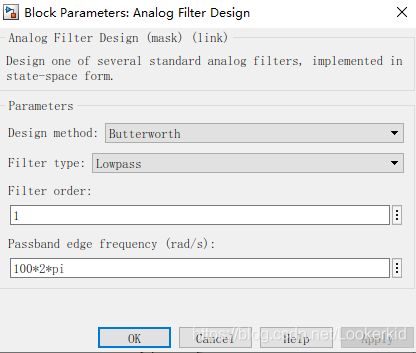
参数设置

设计方法
过滤器设计方法：巴特沃思，I型Chebyshev，II型Chebyshev，椭圆形或Bessel。可调（Simulink）。

过滤器类型
要设计的滤波器类型：低通，高通，带通或带阻。可调（Simulink）。

筛选顺序
滤波器的顺序，适用于低通和高通配置。对于带通和带阻配置，最终滤波器的阶次是该值的两倍。

通带边沿频率
Butterworth，Chebyshev I型，椭圆形和贝塞尔设计的高通和低通配置的通带边沿频率（以弧度/秒为单位）。可调（Simulink）。

较低的通带边缘频率
Butterworth，Chebyshev I型，椭圆形和贝塞尔设计的带通和带阻配置的较低通带频率，以rad / s为单位。可调（Simulink）。

高通带边沿频率
巴特沃思，I型切比雪夫，椭圆形和贝塞尔设计的带通和带阻配置的最高通带频率，以弧度/秒为单位。可调（Simulink）。

阻带边沿频率
Chebyshev II型设计的高通和低通频带配置的阻带边沿频率，以rad / s为单位。可调（Simulink）。

较低的阻带边沿频率
Chebyshev II型设计的带通和带阻配置的较低阻带边沿频率（以rad / s为单位）。可调（Simulink）。

上阻带边沿频率
Chebyshev II型设计的带通和带阻滤波器配置的阻带上限频率，以弧度/秒为单位。可调（Simulink）。

通带纹波，以dB为单位
Chebyshev I型和椭圆形设计的通带纹波，以dB为单位。可调（Simulink）。

阻带衰减（dB）
Chebyshev II型和椭圆形设计的阻带衰减，以dB为单位。可调（Simulink）。

 

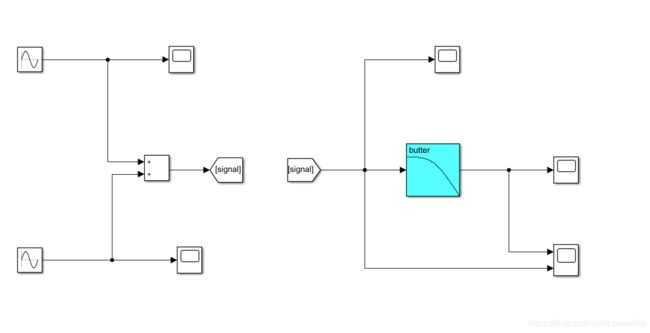
Simulink仿真

 

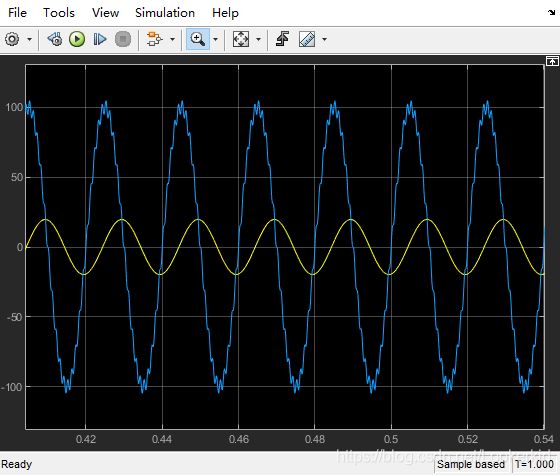
模拟加入谐波噪声的情况

 

信号源

噪声源

 

 

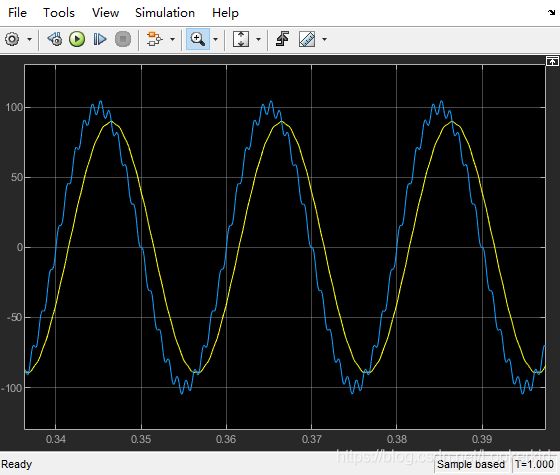
采用butter

输出结果

 

 

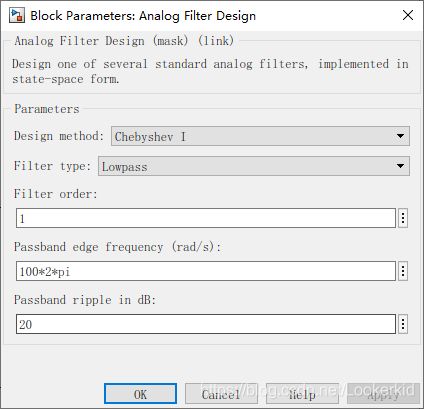
采用chebyI

输出结果

 

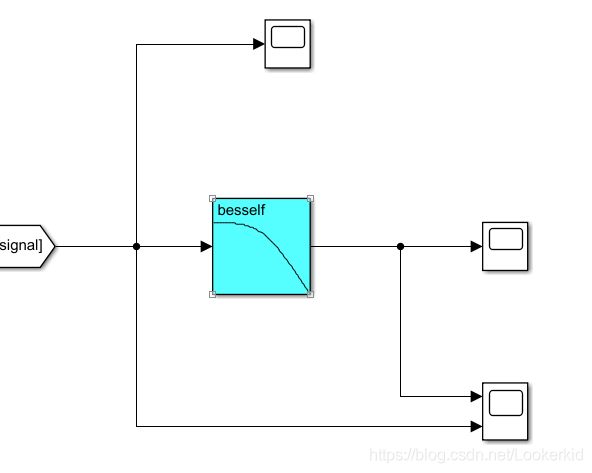
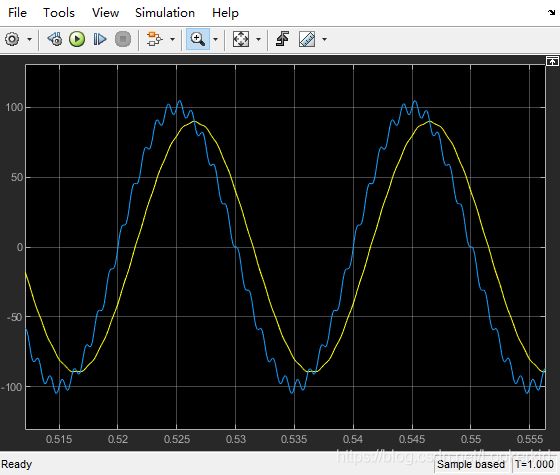
采用besself

输出结果