《动手学深度学习》Task03 ：过拟合、欠拟合及其解决方案；梯度消失、梯度爆炸；循环神经网络进阶

一、模型选择、过拟合和欠拟合

模型选择

验证数据集

从严格意义上讲，测试集只能在所有超参数和模型参数选定后使用一次。不可以使用测试数据选择模型，如调参。由于无法从训练误差估计泛化误差，因此也不应只依赖训练数据选择模型。鉴于此，我们可以预留一部分在训练数据集和测试数据集以外的数据来进行模型选择。这部分数据被称为验证数据集，简称验证集（validation set）。例如，我们可以从给定的训练集中随机选取一小部分作为验证集，而将剩余部分作为真正的训练集。

K折交叉验证

由于验证数据集不参与模型训练，当训练数据不够用时，预留大量的验证数据显得太奢侈。一种改善的方法是K折交叉验证（K-fold cross-validation）。在K折交叉验证中，我们把原始训练数据集分割成K个不重合的子数据集，然后我们做K次模型训练和验证。每一次，我们使用一个子数据集验证模型，并使用其他K-1个子数据集来训练模型。在这K次训练和验证中，每次用来验证模型的子数据集都不同。最后，我们对这K次训练误差和验证误差分别求平均。

过拟合和欠拟合

接下来，我们将探究模型训练中经常出现的两类典型问题：

• 一类是模型无法得到较低的训练误差，我们将这一现象称作欠拟合（underfitting）；
• 另一类是模型的训练误差远小于它在测试数据集上的误差，我们称该现象为过拟合（overfitting）。
  在实践中，我们要尽可能同时应对欠拟合和过拟合。虽然有很多因素可能导致这两种拟合问题，在这里我们重点讨论两个因素：模型复杂度和训练数据集大小。

模型复杂度

为了解释模型复杂度，我们以多项式函数拟合为例。给定一个由标量数据特征$x$和对应的标量标签$y$组成的训练数据集，多项式函数拟合的目标是找一个$K$阶多项式函数

$$\hat{y}=b+\sum _{k=1}^K{x}^k{w}_k$$

来近似 $y$。在上式中，$w_k$是模型的权重参数，$b$是偏差参数。与线性回归相同，多项式函数拟合也使用平方损失函数。特别地，一阶多项式函数拟合又叫线性函数拟合。

给定训练数据集，模型复杂度和误差之间的关系：

训练数据集大小

影响欠拟合和过拟合的另一个重要因素是训练数据集的大小。一般来说，如果训练数据集中样本数过少，特别是比模型参数数量（按元素计）更少时，过拟合更容易发生。此外，泛化误差不会随训练数据集里样本数量增加而增大。因此，在计算资源允许的范围之内，我们通常希望训练数据集大一些，特别是在模型复杂度较高时，例如层数较多的深度学习模型。

二、权重衰减

方法

权重衰减等价于 $L_2$ 范数正则化（regularization）。正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小，是应对过拟合的常用手段。

L2 范数正则化（regularization）

$L_2$范数正则化在模型原损失函数基础上添加$L_2$范数惩罚项，从而得到训练所需要最小化的函数。$L_2$范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。以线性回归中的线性回归损失函数为例

$$\ell (w_1,w_2,b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}{\left(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)}\right)}^2$$

其中$w_1,w_2$是权重参数，$b$是偏差参数，样本$i$的输入为$x_1^{(i)},x_2^{(i)}$，标签为$y^{(i)}$，样本数为$n$。将权重参数用向量$\mathbf{w}=[w_1,w_2]$表示，带有$L_2$范数惩罚项的新损失函数为

$$\ell (w_1,w_2,b)+\frac{\lambda }{2n}|\mathbf{w}{|}^2,$$

其中超参数$\lambda >0$。当权重参数均为0时，惩罚项最小。当$\lambda$较大时，惩罚项在损失函数中的比重较大，这通常会使学到的权重参数的元素较接近0。当$\lambda$设为0时，惩罚项完全不起作用。上式中$L_2$范数平方$|\mathbf{w}{|}^2$展开后得到$w_1^2+w_2^2$。
有了$L_2$范数惩罚项后，在小批量随机梯度下降中，我们将线性回归一节中权重$w_1$和$w_2$的迭代方式更改为

$$\begin{array}{rl}{w}_1& \leftarrow \left(1-\frac{\eta \lambda }{|\mathcal{B}|}\right)w_1-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{x}_1^{(i)}\left(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)}\right),\\ w_2& \leftarrow \left(1-\frac{\eta \lambda }{|\mathcal{B}|}\right)w_2-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{x}_2^{(i)}\left(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)}\right).\end{array}$$

可见，$L_2$范数正则化令权重$w_1$和$w_2$先自乘小于1的数，再减去不含惩罚项的梯度。因此，$L_2$范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制，这可能对过拟合有效。

三、丢弃法

多层感知机中神经网络图描述了一个单隐藏层的多层感知机。其中输入个数为4，隐藏单元个数为5，且隐藏单元$h_i$（$i=1,\dots ,5$）的计算表达式为

$$h_i=\varphi \left(x_1{w}_{1i}+x_2{w}_{2i}+x_3{w}_{3i}+x_4{w}_{4i}+b_i\right)$$

这里$\varphi$是激活函数，$x_1,\dots ,x_4$是输入，隐藏单元$i$的权重参数为$w_{1i},\dots ,w_{4i}$，偏差参数为$b_i$。当对该隐藏层使用丢弃法时，该层的隐藏单元将有一定概率被丢弃掉。设丢弃概率为$p$，那么有$p$的概率$h_i$会被清零，有$1-p$的概率$h_i$会除以$1-p$做拉伸。丢弃概率是丢弃法的超参数。具体来说，设随机变量${\xi }_i$为0和1的概率分别为$p$和$1-p$。使用丢弃法时我们计算新的隐藏单元$h_i^{\prime }$

$$h_i^{\prime }=\frac{{\xi }_i}{1-p}{h}_i$$

由于$E({\xi }_i)=1-p$，因此

$$E(h_i^{\prime })=\frac{E({\xi }_i)}{1-p}{h}_i=h_i$$

即丢弃法不改变其输入的期望值。让我们对之前多层感知机的神经网络中的隐藏层使用丢弃法，一种可能的结果如图所示，其中$h_2$和$h_5$被清零。这时输出值的计算不再依赖$h_2$和$h_5$，在反向传播时，与这两个隐藏单元相关的权重的梯度均为0。由于在训练中隐藏层神经元的丢弃是随机的，即$h_1,\dots ,h_5$都有可能被清零，输出层的计算无法过度依赖$h_1,\dots ,h_5$中的任一个，从而在训练模型时起到正则化的作用，并可以用来应对过拟合。在测试模型时，我们为了拿到更加确定性的结果，一般不使用丢弃法

四、考虑环境因素

协变量偏移

这里我们假设，虽然输入的分布可能随时间而改变，但是标记函数，即条件分布P（y∣x）不会改变。虽然这个问题容易理解，但在实践中也容易忽视。

想想区分猫和狗的一个例子。我们的训练数据使用的是猫和狗的真实的照片，但是在测试时，我们被要求对猫和狗的卡通图片进行分类。

cat	cat	dog	dog

测试数据：

cat	cat	dog	dog

显然，这不太可能奏效。训练集由照片组成，而测试集只包含卡通。在一个看起来与测试集有着本质不同的数据集上进行训练，而不考虑如何适应新的情况，这是不是一个好主意。不幸的是，这是一个非常常见的陷阱。

统计学家称这种协变量变化是因为问题的根源在于特征分布的变化（即协变量的变化）。数学上，我们可以说P（x）改变了，但P（y∣x）保持不变。尽管它的有用性并不局限于此，当我们认为x导致y时，协变量移位通常是正确的假设。

标签偏移

当我们认为导致偏移的是标签P（y）上的边缘分布的变化，但类条件分布是不变的P（x∣y）时，就会出现相反的问题。当我们认为y导致x时，标签偏移是一个合理的假设。例如，通常我们希望根据其表现来预测诊断结果。在这种情况下，我们认为诊断引起的表现，即疾病引起的症状。有时标签偏移和协变量移位假设可以同时成立。例如，当真正的标签函数是确定的和不变的，那么协变量偏移将始终保持，包括如果标签偏移也保持。有趣的是，当我们期望标签偏移和协变量偏移保持时，使用来自标签偏移假设的方法通常是有利的。这是因为这些方法倾向于操作看起来像标签的对象，这（在深度学习中）与处理看起来像输入的对象（在深度学习中）相比相对容易一些。

病因（要预测的诊断结果）导致 症状（观察到的结果）。

训练数据集，数据很少只包含流感p(y)的样本。

而测试数据集有流感p(y)和流感q(y)，其中不变的是流感症状p(x|y)。

概念偏移

另一个相关的问题出现在概念转换中，即标签本身的定义发生变化的情况。这听起来很奇怪，毕竟猫就是猫。的确，猫的定义可能不会改变，但我们能不能对软饮料也这么说呢？事实证明，如果我们周游美国，按地理位置转移数据来源，我们会发现，即使是如图所示的这个简单术语的定义也会发生相当大的概念转变。

$$美国软饮料名称的概念转变$$
如果我们要建立一个机器翻译系统，分布P（y∣x）可能因我们的位置而异。这个问题很难发现。另一个可取之处是P（y∣x）通常只是逐渐变化。

实战

预处理数据

我们对连续数值的特征做标准化（standardization）：设该特征在整个数据集上的均值为$\mu$，标准差为$\sigma$。那么，我们可以将该特征的每个值先减去$\mu$再除以$\sigma$得到标准化后的每个特征值。对于缺失的特征值，我们将其替换成该特征的均值。

numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index
all_features[numeric_features] = all_features[numeric_features].apply(
    lambda x: (x - x.mean()) / (x.std()))
# 标准化后，每个数值特征的均值变为0，所以可以直接用0来替换缺失值
all_features[numeric_features] = all_features[numeric_features].fillna(0)

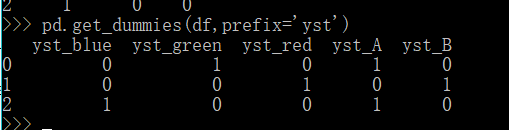
接下来将离散数值转成指示特征。举个例子，假设特征MSZoning里面有两个不同的离散值RL和RM，那么这一步转换将去掉MSZoning特征，并新加两个特征MSZoning_RL和MSZoning_RM，其值为0或1。如果一个样本原来在MSZoning里的值为RL，那么有MSZoning_RL=1且MSZoning_RM=0。

# dummy_na=True将缺失值也当作合法的特征值并为其创建指示特征
all_features = pd.get_dummies(all_features, dummy_na=True)#是利用pandas实现one hot encode的方式
all_features

get_dummies 是利用pandas实现one hot encode的方式。
get_dummies参数如下：

pandas.get_dummies（data，prefix = None，prefix_sep =’_’，dummy_na = False，columns = None，sparse = False，drop_first = False，dtype = None ）

data ： array-like，Series或DataFrame

prefix ：string，字符串列表或字符串dict，默认为None，

用于追加DataFrame列名的字符串。在DataFrame上调用get_dummies时，传递一个长度等于列数的列表。或者，前缀
可以是将列名称映射到前缀的字典。

prefix_sep ： string，默认为’_’

如果附加前缀，分隔符/分隔符要使用。或者传递与前缀一样的列表或字典。

dummy_na ： bool，默认为False 如果忽略False NaN，则添加一列以指示NaN。

columns ： 类似列表，默认为无 要编码的DataFrame中的列名称。如果列是None，那么所有与列 对象或类别 D型细胞将被转换。

sparse ： bool，默认为False 伪编码列是否应由SparseArray（True）或常规NumPy数组（False）支持。

drop_first ： bool，默认为False

是否通过删除第一级别从k分类级别获得k-1个假人。 版本0.18.0中的新功能。

dtype： D型，默认np.uint8

新列的数据类型。只允许一个dtype。 版本0.23.0中的新功能。

例如：

prefix自定义前缀

n_train = train_data.shape[0]
train_features = torch.tensor(all_features[:n_train].values, dtype=torch.float)
test_features = torch.tensor(all_features[n_train:].values, dtype=torch.float)
train_labels = torch.tensor(train_data.SalePrice.values, dtype=torch.float).view(-1, 1)

训练模型

loss = torch.nn.MSELoss()

def get_net(feature_num):
    net = nn.Linear(feature_num, 1)
    for param in net.parameters():
        nn.init.normal_(param, mean=0, std=0.01)
    return net

下面定义比赛用来评价模型的对数均方根误差。给定预测值${\hat{y}}_1,\dots ,{\hat{y}}_n$和对应的真实标签$y_1,\dots ,y_n$，它的定义为

$$\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(\log (y_i)-\log ({\hat{y}}_i)\right)}^2}.$$

对数均方根误差的实现如下。
def log_rmse(net, features, labels):
    with torch.no_grad():
        # 将小于1的值设成1，使得取对数时数值更稳定
        clipped_preds = torch.max(net(features), torch.tensor(1.0))
        rmse = torch.sqrt(2 * loss(clipped_preds.log(), labels.log()).mean())
    return rmse.item()
    
下面的训练函数跟本章中前几节的不同在于使用了Adam优化算法。
相对之前使用的小批量随机梯度下降，它对学习率相对不那么敏感。我们将在之后的“优化算法”一章里详细介绍它。

def train(net, train_features, train_labels, test_features, test_labels,
          num_epochs, learning_rate, weight_decay, batch_size):
    train_ls, test_ls = [], []
    dataset = torch.utils.data.TensorDataset(train_features, train_labels)
    train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True)
    # 这里使用了Adam优化算法
    optimizer = torch.optim.Adam(params=net.parameters(), lr=learning_rate, weight_decay=weight_decay) 
    net = net.float()
    for epoch in range(num_epochs):
        for X, y in train_iter:
            l = loss(net(X.float()), y.float())
            optimizer.zero_grad()
            l.backward()
            optimizer.step()
        train_ls.append(log_rmse(net, train_features, train_labels))
        if test_labels is not None:
            test_ls.append(log_rmse(net, test_features, test_labels))
    return train_ls, test_ls

K折交叉验证

我们在模型选择、欠拟合和过拟合中介绍了$K$折交叉验证。它将被用来选择模型设计并调节超参数。下面实现了一个函数，它返回第i折交叉验证时所需要的训练和验证数据。

def get_k_fold_data(k, i, X, y):
    # 返回第i折交叉验证时所需要的训练和验证数据
    assert k > 1
    fold_size = X.shape[0] // k
    X_train, y_train = None, None
    for j in range(k):
        idx = slice(j * fold_size, (j + 1) * fold_size)
        X_part, y_part = X[idx, :], y[idx]
        if j == i:
            X_valid, y_valid = X_part, y_part
        elif X_train is None:
            X_train, y_train = X_part, y_part
        else:
            X_train = torch.cat((X_train, X_part), dim=0)
            y_train = torch.cat((y_train, y_part), dim=0)
    return X_train, y_train, X_valid, y_valid

在$K$折交叉验证中我们训练K次并返回训练和验证的平均误差
def k_fold(k, X_train, y_train, num_epochs,
           learning_rate, weight_decay, batch_size):
    train_l_sum, valid_l_sum = 0, 0
    for i in range(k):
        data = get_k_fold_data(k, i, X_train, y_train)
        net = get_net(X_train.shape[1])
        train_ls, valid_ls = train(net, *data, num_epochs, learning_rate,
                                   weight_decay, batch_size)
        train_l_sum += train_ls[-1]
        valid_l_sum += valid_ls[-1]
        if i == 0:
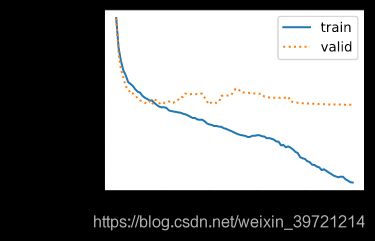
            d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'rmse',
                         range(1, num_epochs + 1), valid_ls,
                         ['train', 'valid'])
        print('fold %d, train rmse %f, valid rmse %f' % (i, train_ls[-1], valid_ls[-1]))
    return train_l_sum / k, valid_l_sum / k

模型选择

我们使用一组未经调优的超参数并计算交叉验证误差。可以改动这些超参数来尽可能减小平均测试误差。
有时候你会发现一组参数的训练误差可以达到很低，但是在$K$折交叉验证上的误差可能反而较高。这种现象很可能是由过拟合造成的。因此，当训练误差降低时，我们要观察$K$折交叉验证上的误差是否也相应降低。

k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr, weight_decay, batch_size)
print('%d-fold validation: avg train rmse %f, avg valid rmse %f' % (k, train_l, valid_l))

fold 0, train rmse 11.088140, valid rmse 11.782319
fold 1, train rmse 10.919130, valid rmse 11.572948
fold 2, train rmse 11.212792, valid rmse 11.891768
fold 3, train rmse 11.143944, valid rmse 11.985317
fold 4, train rmse 11.262851, valid rmse 11.829272
5-fold validation: avg train rmse 11.125372, avg valid rmse 11.812325

预测并在Kaggle中提交结果

下面定义预测函数。在预测之前，我们会使用完整的训练数据集来重新训练模型，并将预测结果存成提交所需要的格式。

def train_and_pred(train_features, test_features, train_labels, test_data,
                   num_epochs, lr, weight_decay, batch_size):
    net = get_net(train_features.shape[1])
    train_ls, _ = train(net, train_features, train_labels, None, None,
                        num_epochs, lr, weight_decay, batch_size)
    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'rmse')
    print('train rmse %f' % train_ls[-1])
    preds = net(test_features).detach().numpy()
    test_data['SalePrice'] = pd.Series(preds.reshape(1, -1)[0])
    submission = pd.concat([test_data['Id'], test_data['SalePrice']], axis=1)
    submission.to_csv('./submission.csv', index=False)
    # sample_submission_data = pd.read_csv("../input/house-prices-advanced-regression-techniques/sample_submission.csv")

设计好模型并调好超参数之后，下一步就是对测试数据集上的房屋样本做价格预测。
如果我们得到与交叉验证时差不多的训练误差，那么这个结果很可能是理想的，可以在Kaggle上提交结果。
train_and_pred(train_features, test_features, train_labels, test_data, num_epochs, lr, weight_decay, batch_size)

五、循环神经网络

本节介绍循环神经网络，下图展示了如何基于循环神经网络实现语言模型。我们的目的是基于当前的输入与过去的输入序列，预测序列的下一个字符。循环神经网络引入一个隐藏变量$H$，用$H_t$表示$H$在时间步$t$的值。$H_t$的计算基于$X_t$和$H_{t-1}$，可以认为$H_t$记录了到当前字符为止的序列信息，利用$H_t$对序列的下一个字符进行预测。

循环神经网络的构造

我们先看循环神经网络的具体构造。假设${\mathbf{X}}_t\in {\mathbb{R}}^{n\times d}$是时间步$t$的小批量输入，${\mathbf{H}}_t\in {\mathbb{R}}^{n\times h}$是该时间步的隐藏变量，则：

$${\mathbf{H}}_t=\varphi ({\mathbf{X}}_t{\mathbf{W}}_{xh}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hh}+{\mathbf{b}}_h).$$

其中，${\mathbf{W}}_{xh}\in {\mathbb{R}}^{d\times h}$，${\mathbf{W}}_{hh}\in {\mathbb{R}}^{h\times h}$，${\mathbf{b}}_h\in {\mathbb{R}}^{1\times h}$，$\varphi$函数是非线性激活函数。由于引入了${\mathbf{H}}_{t-1}{\mathbf{W}}_{hh}$，$H_t$能够捕捉截至当前时间步的序列的历史信息，就像是神经网络当前时间步的状态或记忆一样。由于$H_t$的计算基于$H_{t-1}$，上式的计算是循环的，使用循环计算的网络即循环神经网络（recurrent neural network）。

在时间步$t$，输出层的输出为：

$${\mathbf{O}}_t={\mathbf{H}}_t{\mathbf{W}}_{hq}+{\mathbf{b}}_q.$$

其中${\mathbf{W}}_{hq}\in {\mathbb{R}}^{h\times q}$，${\mathbf{b}}_q\in {\mathbb{R}}^{1\times q}$。

从零开始实现循环神经网络

我们先尝试从零开始实现一个基于字符级循环神经网络的语言模型，这里我们使用周杰伦的歌词作为语料，首先我们读入数据：

import torch
import torch.nn as nn
import time
import math
import sys
sys.path.append("/home/kesci/input")
import d2l_jay9460 as d2l
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = d2l.load_data_jay_lyrics()
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

def one_hot(x, n_class, dtype=torch.float32):
    result = torch.zeros(x.shape[0], n_class, dtype=dtype, device=x.device)  # shape: (n, n_class)
    result.scatter_(1, x.long().view(-1, 1), 1)  # result[i, x[i, 0]] = 1
    return result
    
x = torch.tensor([0, 2])
x_one_hot = one_hot(x, vocab_size)
print(x_one_hot)
print(x_one_hot.shape)
print(x_one_hot.sum(axis=1))

－－－－－－－－－－－－－－－－－－－－－－－－
tensor([[1., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 1.,  ..., 0., 0., 0.]])
torch.Size([2, 1027])
tensor([1., 1.])

scatter_(input, dim, index, src)将src中数据根据index中的索引按照dim的方向填进input中.

1 >>> x = torch.rand(2, 5)
2 >>> x
3 
4  0.4319  0.6500  0.4080  0.8760  0.2355
5  0.2609  0.4711  0.8486  0.8573  0.1029
6 [torch.FloatTensor of size 2x5]

1. dim = 0，分别对每列填充：

>>> torch.zeros(3, 5).scatter_(0, torch.LongTensor([[0, 1, 2, 0, 0], [2, 0, 0, 1, 2]]), x)

 0.4319  0.4711  0.8486  0.8760  0.2355
 0.0000  0.6500  0.0000  0.8573  0.0000
 0.2609  0.0000  0.4080  0.0000  0.1029
[torch.FloatTensor of size 3x5]

实现原理：

对于LoneTensor内的矩阵，暂且称为 tmp = [[0, 1, 2, 0, 0], [2, 0, 0, 1, 2]]；将最终的 3*5的矩阵，暂且称为result。result初始为全0，需要经过scatter_处理。

举例：

对于tmp[0][0] = 0 -> 取x中x[0][0] = 0.4319，将其插入到result第0列的第0个位置，result[0][0] = 0.4319；

对于tmp[0][1] = 1 -> 取x中x[0][1] = 0.6500，将其插入到result第1列的第1个位置，result[1][1] = 0.6500；

对于tmp[0][2] = 2 -> 取x中x[0][1] = 0.4080，将其插入到result第2列的第2个位置，result[2][2] = 0.4080；

…

对于tmp[1][0] = 2 -> 取x中x[1][0] = 0.2609，将其插入到result第0列的第2个位置，result[2][0] = 0.2609；

对于tmp[1][1] = 0 -> 取x中x[1][1] = 0.4711，将其插入到result第1列的第0个位置，result[0][1] = 0.4711。

…

2. dim = 1，分别对每行填充

1 >>> z = torch.zeros(2, 4).scatter_(1, torch.LongTensor([[2], [3]]), 1.23)
2 >>> z
3 
4  0.0000  0.0000  1.2300  0.0000
5  0.0000  0.0000  0.0000  1.2300
6 [torch.FloatTensor of size 2x4]

tmp = [[2], [3]]

tmp[0][0] = 2 -> 取x中x[0][0] = 0.4319，将其插入到result第0行的第2个位置，result[0][2] = 0.4319；

…

我们每次采样的小批量的形状是（批量大小, 时间步数）。下面的函数将这样的小批量变换成数个形状为（批量大小, 词典大小）的矩阵，矩阵个数等于时间步数。也就是说，时间步$t$的输入为${\mathbf{X}}_t\in {\mathbb{R}}^{n\times d}$，其中$n$为批量大小，$d$为词向量大小，即one-hot向量长度（词典大小）。

def to_onehot(X, n_class):
    return [one_hot(X[:, i], n_class) for i in range(X.shape[1])]

X = torch.arange(10).view(2, 5)
inputs = to_onehot(X, vocab_size)
print(len(inputs), inputs[0].shape)

5 torch.Size([2, 1027])//5个时间步，批量大小为２

初始化模型参数

num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
# num_inputs: d
# num_hiddens: h, 隐藏单元的个数是超参数
# num_outputs: q

def get_params():
    def _one(shape):
        param = torch.zeros(shape, device=device, dtype=torch.float32)
        nn.init.normal_(param, 0, 0.01)
        return torch.nn.Parameter(param)

    # 隐藏层参数
    W_xh = _one((num_inputs, num_hiddens))
    W_hh = _one((num_hiddens, num_hiddens))
    b_h = torch.nn.Parameter(torch.zeros(num_hiddens, device=device))
    # 输出层参数
    W_hq = _one((num_hiddens, num_outputs))
    b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device))
    return (W_xh, W_hh, b_h, W_hq, b_q)

定义模型

函数rnn用循环的方式依次完成循环神经网络每个时间步的计算。

def rnn(inputs, state, params):
    # inputs和outputs皆为num_steps个形状为(batch_size, vocab_size)的矩阵
    W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    for X in inputs:
        H = torch.tanh(torch.matmul(X, W_xh) + torch.matmul(H, W_hh) + b_h)
        Y = torch.matmul(H, W_hq) + b_q
        outputs.append(Y)
    return outputs, (H,)


函数init_rnn_state初始化隐藏变量，这里的返回值是一个元组。

def init_rnn_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device), )

做个简单的测试来观察输出结果的个数（时间步数），以及第一个时间步的输出层输出的形状和隐藏状态的形状。

print(X.shape)
print(num_hiddens)
print(vocab_size)
state = init_rnn_state(X.shape[0], num_hiddens, device)
inputs = to_onehot(X.to(device), vocab_size)
params = get_params()
outputs, state_new = rnn(inputs, state, params)
print(len(inputs), inputs[0].shape)
print(len(outputs), outputs[0].shape)
print(len(state), state[0].shape)
print(len(state_new), state_new[0].shape)


－－－－－－－－－－－－－－－－－－－－－－－

torch.Size([2, 5])
256
1027
5 torch.Size([2, 1027])
5 torch.Size([2, 1027])//每步输入预测一个输出
1 torch.Size([2, 256])
1 torch.Size([2, 256])

裁剪梯度

循环神经网络中较容易出现梯度衰减或梯度爆炸，这会导致网络几乎无法训练。裁剪梯度（clip gradient）是一种应对梯度爆炸的方法。假设我们把所有模型参数的梯度拼接成一个向量 $\mathbf{g}$，并设裁剪的阈值是$\theta$。裁剪后的梯度

$$\min \left(\frac{\theta }{\Vert \mathbf{g}\Vert },1\right)\mathbf{g}$$

的$L_2$范数不超过$\theta$。

def grad_clipping(params, theta, device):
    norm = torch.tensor([0.0], device=device)
    for param in params:
        norm += (param.grad.data ** 2).sum()
    norm = norm.sqrt().item()
    if norm > theta:
        for param in params:
            param.grad.data *= (theta / norm)

定义预测函数

(将上一时间步的输出作为当前时间步的输入)
以下函数基于前缀prefix（含有数个字符的字符串）来预测接下来的num_chars个字符。这个函数稍显复杂，其中我们将循环神经单元rnn设置成了函数参数，这样在后面小节介绍其他循环神经网络时能重复使用这个函数。

def predict_rnn(prefix, num_chars, rnn, params, init_rnn_state,
                num_hiddens, vocab_size, device, idx_to_char, char_to_idx):
    state = init_rnn_state(1, num_hiddens, device)
    output = [char_to_idx[prefix[0]]]   # output记录prefix加上预测的num_chars个字符
    for t in range(num_chars + len(prefix) - 1):
        # 将上一时间步的输出作为当前时间步的输入
        X = to_onehot(torch.tensor([[output[-1]]], device=device), vocab_size)
        # 计算输出和更新隐藏状态
        (Y, state) = rnn(X, state, params)
        # 下一个时间步的输入是prefix里的字符或者当前的最佳预测字符
        if t < len(prefix) - 1:
            output.append(char_to_idx[prefix[t + 1]])
        else:
            output.append(Y[0].argmax(dim=1).item())
    return ''.join([idx_to_char[i] for i in output])

我们先测试一下`predict_rnn`函数。我们将根据前缀“分开”创作长度为10个字符（不考虑前缀长度）的一段歌词。因为模型参数为随机值，所以预测结果也是随机的。

predict_rnn('分开', 10, rnn, params, init_rnn_state, num_hiddens, vocab_size,
            device, idx_to_char, char_to_idx)

－－－－－－－－－－－－－－－－－－－
'分开濡时食提危踢拆田唱母'

困惑度

我们通常使用困惑度（perplexity）来评价语言模型的好坏。回忆一下“softmax回归”一节中交叉熵损失函数的定义。困惑度是对交叉熵损失函数做指数运算后得到的值。特别地，

• 最佳情况下，模型总是把标签类别的概率预测为1，此时困惑度为1；
• 最坏情况下，模型总是把标签类别的概率预测为0，此时困惑度为正无穷；
• 基线情况下，模型总是预测所有类别的概率都相同，此时困惑度为类别个数。

显然，任何一个有效模型的困惑度必须小于类别个数。在本例中，困惑度必须小于词典大小vocab_size。

定义模型训练函数

跟之前章节的模型训练函数相比，这里的模型训练函数有以下几点不同：

1. 使用困惑度评价模型。
2. 在迭代模型参数前裁剪梯度。
3. 对时序数据采用不同采样方法将导致隐藏状态初始化的不同。

def train_and_predict_rnn(rnn, get_params, init_rnn_state, num_hiddens,
                          vocab_size, device, corpus_indices, idx_to_char,
                          char_to_idx, is_random_iter, num_epochs, num_steps,
                          lr, clipping_theta, batch_size, pred_period,
                          pred_len, prefixes):
    if is_random_iter:
        data_iter_fn = d2l.data_iter_random
    else:
        data_iter_fn = d2l.data_iter_consecutive
    params = get_params()
    loss = nn.CrossEntropyLoss()

    for epoch in range(num_epochs):
        if not is_random_iter:  # 如使用相邻采样，在epoch开始时初始化隐藏状态
            state = init_rnn_state(batch_size, num_hiddens, device)
        l_sum, n, start = 0.0, 0, time.time()
        data_iter = data_iter_fn(corpus_indices, batch_size, num_steps, device)
        for X, Y in data_iter:
            if is_random_iter:  # 如使用随机采样，在每个小批量更新前初始化隐藏状态
                state = init_rnn_state(batch_size, num_hiddens, device)
            else:  # 否则需要使用detach函数从计算图分离隐藏状态
                for s in state:
                    s.detach_()
            # inputs是num_steps个形状为(batch_size, vocab_size)的矩阵
            inputs = to_onehot(X, vocab_size)
            # outputs有num_steps个形状为(batch_size, vocab_size)的矩阵
            (outputs, state) = rnn(inputs, state, params)
            # 拼接之后形状为(num_steps * batch_size, vocab_size)
            outputs = torch.cat(outputs, dim=0)
            # Y的形状是(batch_size, num_steps)，转置后再变成形状为
            # (num_steps * batch_size,)的向量，这样跟输出的行一一对应
            y = torch.flatten(Y.T)
            # 使用交叉熵损失计算平均分类误差
            l = loss(outputs, y.long())
            
            # 梯度清0
            if params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()
            l.backward()
            grad_clipping(params, clipping_theta, device)  # 裁剪梯度
            d2l.sgd(params, lr, 1)  # 因为误差已经取过均值，梯度不用再做平均
            l_sum += l.item() * y.shape[0]
            n += y.shape[0]

        if (epoch + 1) % pred_period == 0:
            print('epoch %d, perplexity %f, time %.2f sec' % (
                epoch + 1, math.exp(l_sum / n), time.time() - start))
            for prefix in prefixes:
                print(' -', predict_rnn(prefix, pred_len, rnn, params, init_rnn_state,
                    num_hiddens, vocab_size, device, idx_to_char, char_to_idx))

循环神经网络的简介实现

定义模型

我们使用Pytorch中的nn.RNN来构造循环神经网络。在本节中，我们主要关注nn.RNN的以下几个构造函数参数：

• input_size - The number of expected features in the input x
• hidden_size – The number of features in the hidden state h
• nonlinearity – The non-linearity to use. Can be either ‘tanh’ or ‘relu’. Default: ‘tanh’
• batch_first – If True, then the input and output tensors are provided as (batch_size, num_steps, input_size). Default: False

这里的batch_first决定了输入的形状，我们使用默认的参数False，对应的输入形状是 (num_steps, batch_size, input_size)。

forward函数的参数为：

• input of shape (num_steps, batch_size, input_size): tensor containing the features of the input sequence.
• h_0 of shape (num_layers * num_directions, batch_size, hidden_size): tensor containing the initial hidden state for each element in the batch. Defaults to zero if not provided. If the RNN is bidirectional, num_directions should be 2, else it should be 1.

forward函数的返回值是：

• output of shape (num_steps, batch_size, num_directions * hidden_size): tensor containing the output features (h_t) from the last layer of the RNN, for each t.
• h_n of shape (num_layers * num_directions, batch_size, hidden_size): tensor containing the hidden state for t = num_steps.

现在我们构造一个nn.RNN实例，并用一个简单的例子来看一下输出的形状。

rnn_layer = nn.RNN(input_size=vocab_size, hidden_size=num_hiddens)
num_steps, batch_size = 35, 2
X = torch.rand(num_steps, batch_size, vocab_size)
state = None
Y, state_new = rnn_layer(X, state)
print(Y.shape, state_new.shape)


class RNNModel(nn.Module):
    def __init__(self, rnn_layer, vocab_size):
        super(RNNModel, self).__init__()
        self.rnn = rnn_layer
        self.hidden_size = rnn_layer.hidden_size * (2 if rnn_layer.bidirectional else 1) 
        self.vocab_size = vocab_size
        self.dense = nn.Linear(self.hidden_size, vocab_size)

    def forward(self, inputs, state):
        # inputs.shape: (batch_size, num_steps)
        X = to_onehot(inputs, vocab_size)
        X = torch.stack(X)  # X.shape: (num_steps, batch_size, vocab_size)
        hiddens, state = self.rnn(X, state)
        hiddens = hiddens.view(-1, hiddens.shape[-1])  # hiddens.shape: (num_steps * batch_size, hidden_size)
        output = self.dense(hiddens)
        return output, state


类似的，我们需要实现一个预测函数，与前面的区别在于前向计算和初始化隐藏状态。

def predict_rnn_pytorch(prefix, num_chars, model, vocab_size, device, idx_to_char,
                      char_to_idx):
    state = None
    output = [char_to_idx[prefix[0]]]  # output记录prefix加上预测的num_chars个字符
    for t in range(num_chars + len(prefix) - 1):
        X = torch.tensor([output[-1]], device=device).view(1, 1)
        (Y, state) = model(X, state)  # 前向计算不需要传入模型参数
        if t < len(prefix) - 1:
            output.append(char_to_idx[prefix[t + 1]])
        else:
            output.append(Y.argmax(dim=1).item())
    return ''.join([idx_to_char[i] for i in output])

model = RNNModel(rnn_layer, vocab_size).to(device)
predict_rnn_pytorch('分开', 10, model, vocab_size, device, idx_to_char, char_to_idx)
--------------------------
'分开胸呵以轮轮轮轮轮轮轮'

接下来实现训练函数，这里只使用了相邻采样。

def train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
                                corpus_indices, idx_to_char, char_to_idx,
                                num_epochs, num_steps, lr, clipping_theta,
                                batch_size, pred_period, pred_len, prefixes):
    loss = nn.CrossEntropyLoss()
    optimizer = torch.optim.Adam(model.parameters(), lr=lr)
    model.to(device)
    for epoch in range(num_epochs):
        l_sum, n, start = 0.0, 0, time.time()
        data_iter = d2l.data_iter_consecutive(corpus_indices, batch_size, num_steps, device) # 相邻采样
        state = None
        for X, Y in data_iter:
            if state is not None:
                # 使用detach函数从计算图分离隐藏状态
                if isinstance (state, tuple): # LSTM, state:(h, c)  
                    state[0].detach_()
                    state[1].detach_()
                else: 
                    state.detach_()
            (output, state) = model(X, state) # output.shape: (num_steps * batch_size, vocab_size)
            y = torch.flatten(Y.T)
            l = loss(output, y.long())
            
            optimizer.zero_grad()
            l.backward()
            grad_clipping(model.parameters(), clipping_theta, device)
            optimizer.step()
            l_sum += l.item() * y.shape[0]
            n += y.shape[0]
        

        if (epoch + 1) % pred_period == 0:
            print('epoch %d, perplexity %f, time %.2f sec' % (
                epoch + 1, math.exp(l_sum / n), time.time() - start))
            for prefix in prefixes:
                print(' -', predict_rnn_pytorch(
                    prefix, pred_len, model, vocab_size, device, idx_to_char,
                    char_to_idx))


num_epochs, batch_size, lr, clipping_theta = 250, 32, 1e-3, 1e-2
pred_period, pred_len, prefixes = 50, 50, ['分开', '不分开']
train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
                            corpus_indices, idx_to_char, char_to_idx,
                            num_epochs, num_steps, lr, clipping_theta,
                            batch_size, pred_period, pred_len, prefixes)

-------------------------------------------------

epoch 50, perplexity 9.405654, time 0.52 sec
 - 分开始一起 三步四步望著天 看星星 一颗两颗三颗四颗 连成线背著背默默许下心愿  一枝杨柳 你的那我 在
 - 不分开 爱情你的手 一人的老斑鸠 腿短毛不多 快使用双截棍 哼哼哈兮 快使用双截棍 哼哼哈兮 快使用双截棍
epoch 100, perplexity 1.255020, time 0.54 sec
 - 分开 我人了的屋我 一定令它心仪的母斑鸠 爱像一阵风 吹完美主  这样 还人的太快就是学怕眼口让我碰恨这
 - 不分开不想我多的脑袋有问题 随便说说 其实我早已经猜透看透不想多说 只是我怕眼泪撑不住 不懂 你的黑色幽默
epoch 150, perplexity 1.064527, time 0.53 sec
 - 分开 我轻外的溪边 默默在一心抽离 有话不知不觉 一场悲剧 我对不起 藤蔓植物的爬满了伯爵的坟墓 古堡里
 - 不分开不想不多的脑 有教堂有你笑 我有多烦恼  没有你烦 有有样 别怪走 快后悔没说你 我不多难熬 我想就
epoch 200, perplexity 1.033074, time 0.53 sec
 - 分开 我轻外的溪边 默默在一心向昏 的愿  古无着我只能 一个黑远 这想太久 这样我 不要再是你打我妈妈
 - 不分开你只会我一起睡著 样 娘子却只想你和汉堡 我想要你的微笑每天都能看到  我知道这里很美但家乡的你更美
epoch 250, perplexity 1.047890, time 0.68 sec
 - 分开 我轻多的漫 却已在你人演  想要再直你 我想要这样牵着你的手不放开 爱可不可以简简单单没有伤害 你
 - 不分开不想不多的假  已无能为力再提起 决定中断熟悉 然后在这里 不限日期 然后将过去 慢慢温习 让我爱上